
Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания

Прикладные задачи динамики ледяного покрова
Козин В. М., Жесткая В. Д., Погорелова А. В., Чижиумов С. Д., Джабраилов М. Р., Морозов В. С., Кустов А. Н.,
2.1.2. Уравнение малых колебаний плавающей вязко - упругой ледяной пластины, рассматриваемой как общая модель, построенная из тел Максвелла и Кельвина, соединенных последовательно
Рассматривается бесконечная область, покрытая сплошным льдом, по которой со скоростью u перемещается заданная система поверхностных давлений q. Система координат располагается следующим образом: плоскость xOy совпадает с невозмущенной поверхностью раздела лед-вода, ось x направлена в сторону движения судна, ось z - вертикально вверх. Предполагается, что вода - идеальная несжимаемая жидкость плотностью , движение жидкости потенциальное. Ледяной покров моделируется вязко-упругой, изначально ненапряженной однородной изотропной пластиной.
В общем случае уравнение малых колебаний плавающей вязко-упругой ледяной пластины записывается так [124, 127]:
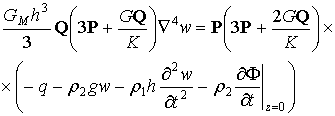 (2.5)
(2.5)
Здесь GМ – модуль упругости при сдвиге; ![]() ; К – модуль всестороннего сжатия; P и Q – линейные дифференциальные операторы, выбираемые в зависимости от принятой для льда реологической модели [122]; h(x,y) – толщина льда; r1(x,y) – плотность льда; w(x,y) – деформация поверхности жидкости или вертикальное перемещение льда; F=F(x,y,z,t) - функция потенциала скорости жидкости, удовлетворяющая уравнению Лапласа
; К – модуль всестороннего сжатия; P и Q – линейные дифференциальные операторы, выбираемые в зависимости от принятой для льда реологической модели [122]; h(x,y) – толщина льда; r1(x,y) – плотность льда; w(x,y) – деформация поверхности жидкости или вертикальное перемещение льда; F=F(x,y,z,t) - функция потенциала скорости жидкости, удовлетворяющая уравнению Лапласа ![]() .
.
Если в качестве линейной вязко-упругой среды, имитирующей лед, взять среду, полученную из тел Максвелла и Кельвина, соединенных последовательно, то пренебрегая упругой сжимаемостью льда (![]() ), можно получить вместо (2.5) следующее упрощенное выражение:
), можно получить вместо (2.5) следующее упрощенное выражение:
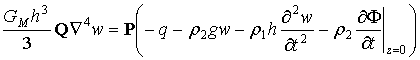 , (2.6)
, (2.6)
где согласно [121, 122] линейные дифференциальные операторы P и Q будут иметь вид:
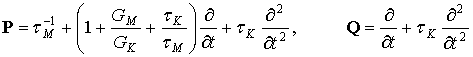 (2.7)
(2.7)
Здесь GM и GK – модули упругости при сдвиге для моделей Максвелла и Кельвина-Фойгта соответственно,![]() и
и ![]() соответствующие времена релаксации.
соответствующие времена релаксации.
Для упрощения математической постановки задачи вводится новая система координат, совмещенная с движущейся нагрузкой:
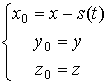 .
.
Тогда
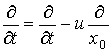
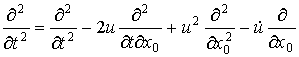 ,
,
а уравнение (2.6) перепишется в новых координатах:
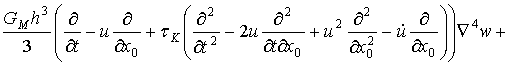
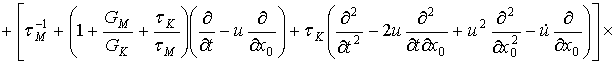
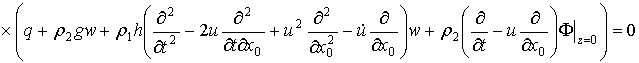 .
.
В стационаре это уравнение примет вид:
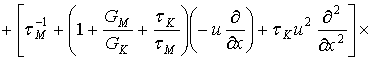
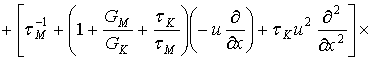
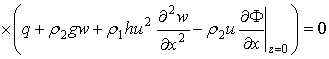 (2.8)
(2.8)
в котором у переменной x опущены нули.
Граничное условие на дне водоема имеет вид:
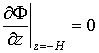 (2.9)
(2.9)
где H=H1-b; H1 – глубина водоема; b=r1h/r2 – глубина погружения льда при статическом равновесии. Для больших глубин, когда H1 намного больше h, можно считать H » H1. В дальнейшем предполагается, что величины r1 и h – постоянные.
Линеаризованное кинематическое условие на поверхности раздела лед-вода имеет вид:
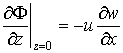 (2.10)
(2.10)