Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
Прикладные задачи динамики ледяного покрова
Козин В. М., Жесткая В. Д., Погорелова А. В., Чижиумов С. Д., Джабраилов М. Р., Морозов В. С., Кустов А. Н.,
2.1.3. Аналитическое решение для прогиба пластины
Представим все задействованные в уравнении (2.8) функции в виде интегралов Фурье:
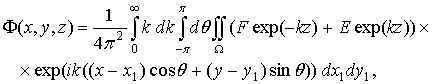
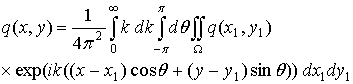
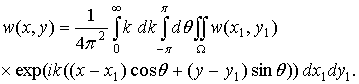(2.11)
Из граничного условия (2.9) получаем
,
а выражение (2.11) для F примет вид:
.
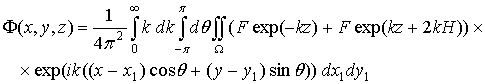Далее используя кинематическое условие (2.10), выразим все величины в (2.8) с учетом (2.11) через одну функцию w. Рассмотрим:
.
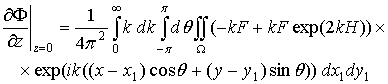
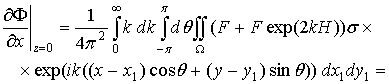
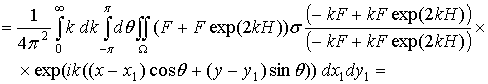
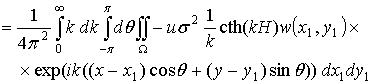где 
. Аналогично можно получить из выражения (2.11) для w следующие выражения:
.
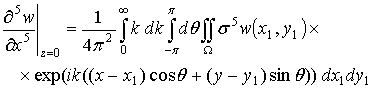
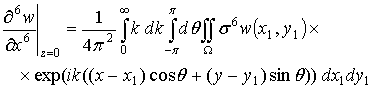
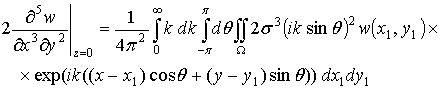
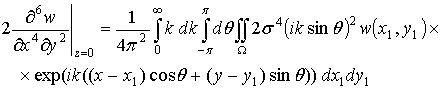
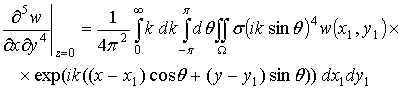
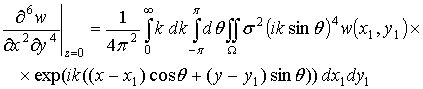
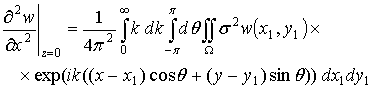
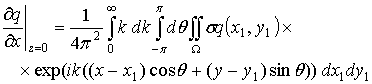
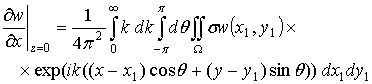
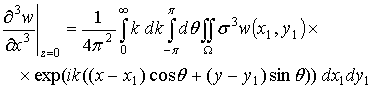
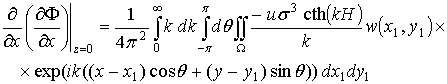
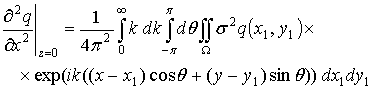
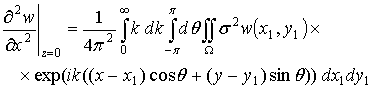
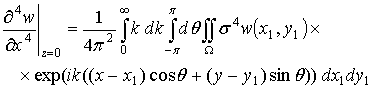
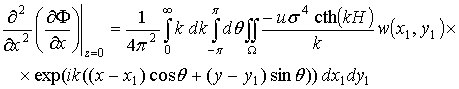Подставляя все полученные результаты в (2.8), можно получить следующее выражение для подынтегральных функций:
.
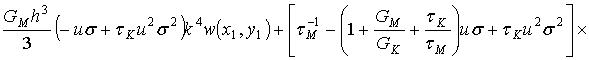
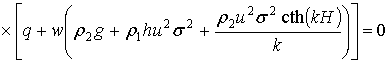Сгруппируем слагаемые с w и q.
.
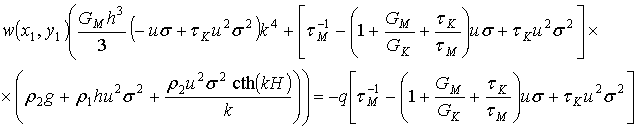Отсюда получим выражение для w(x,y):
.
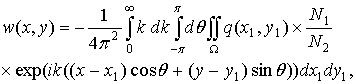где величины N1, N2 имеют вид
.
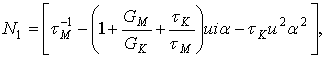
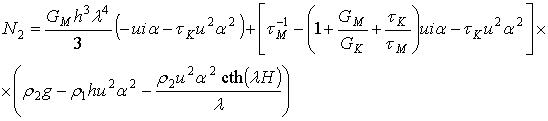Сделаем замену переменных: 
. Тогда вместо одного интеграла от -p до p по переменной q будет два интеграла от -l до l по переменной a, а выражение для w перепишется как
.
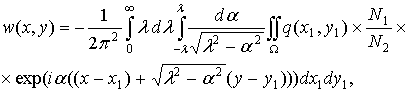где величины N1, N2 имеют вид
.
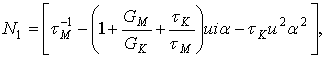
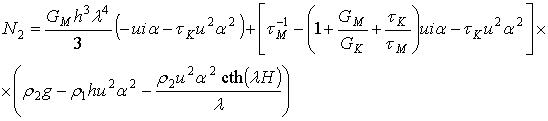После несложных упрощений выражение для w примет вид
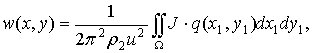(2.12)
.
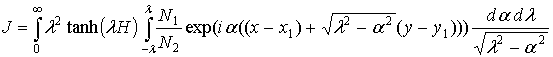
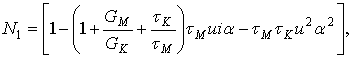
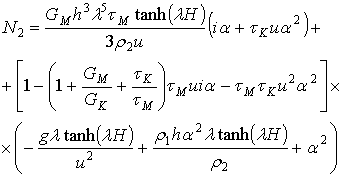Далее необходимо выделить действительную и мнимую части во внутреннем интеграле J с использованием формулы Эйлера 
. Действительная u1 и v1 мнимая части числителя будут иметь вид:
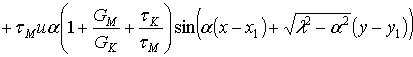, (2.13)
.
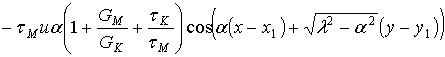Аналогично выделим в знаменателе действительную u2 и мнимую v2 части:
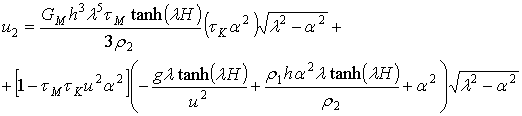(2.14)
.
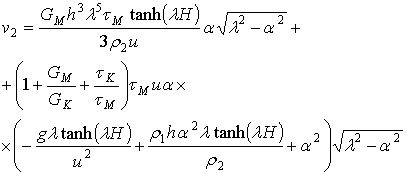Используя формулу комплексных функций
,
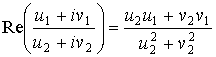получаем
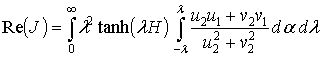, (2.15)
где функции u1, u2, v1, v2 имеют вид (2.13) и (2.14). С учетом того, что в знаменателе стоят только четные функции по переменной a, выделим в числителе тоже четные функции по переменной a, так как нечетные при интегрировании по a дадут нулевое значение интеграла. Для этого используем формулы разложения косинуса суммы и синуса суммы.
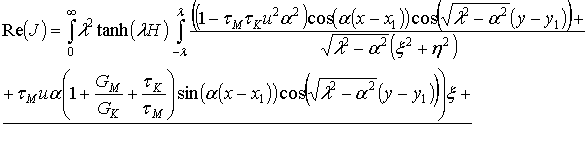
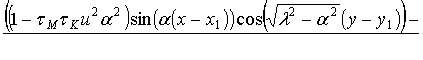(2.16)
,
.
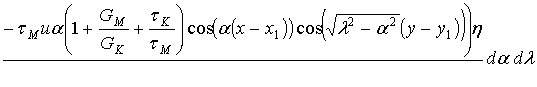
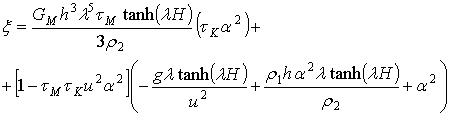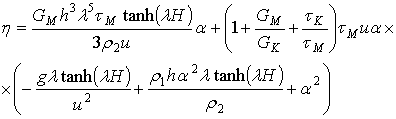После подстановки (2.16) в (2.12) необходимо будет находить интегралы по области распределенной нагрузки W по переменным x и y. Предположим, что давление q является постоянным на прямоугольнике , . Тогда получим:
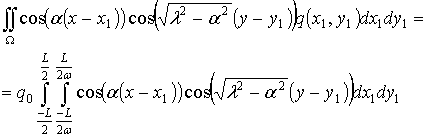
Если в последнем интеграле оставить только четные функции по переменным x1, y1, то можно получить
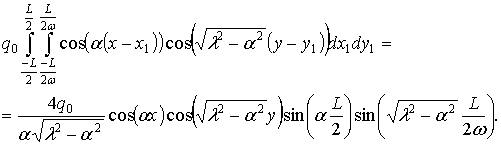(2.17)
Аналогично можно получить
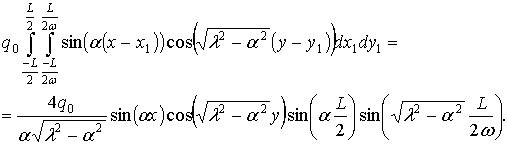(2.18)
С учетом формул (2.16)-(2.18) выражение (2.12) примет вид:
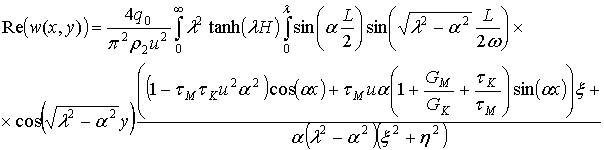
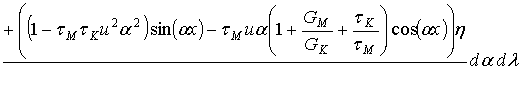(2.19)
,
.
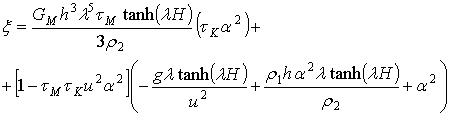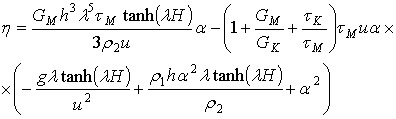Рассмотрим случай, когда в качестве системы перемещающихся давлений
по аналогии с [60,139] берется функция
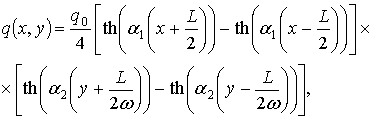(2.20)
где q0 – номинальное давление; L – длина судна; 
- удлинение судна; В – ширина судна; 
- параметры, характеризующие степень отклонения распределения давления в продольном и поперечном направлениях от прямоугольной формы. Чем больше по величине, тем ближе форма распределения давления к прямоугольной. При
q эквивалентно q0, равномерно распределенному по прямоугольнику.
Для заданной формы давления (2.20) по аналогии с [63,139] можно получить следующие формулы:
.
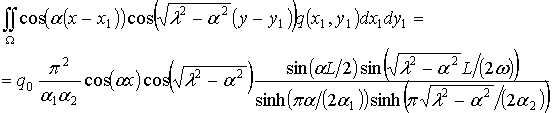
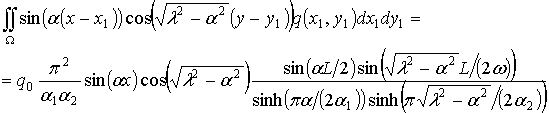И тогда итоговая формула запишется в виде:
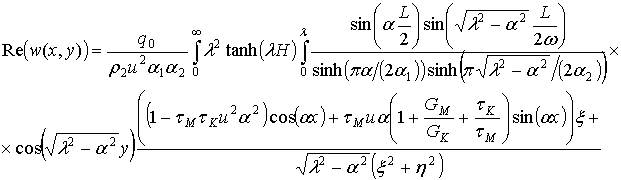
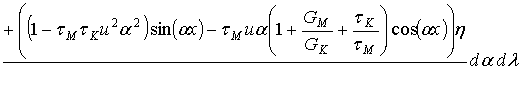, (2.21)
где величины x и h вычисляются по формуле (2.19).