Научная электронная библиотека

Монографии, изданные в издательстве Российской Академии Естествознания

Прикладные задачи динамики ледяного покрова

Козин В. М., Жесткая В. Д., Погорелова А. В., Чижиумов С. Д., Джабраилов М. Р., Морозов В. С., Кустов А. Н.,

2.1.4. Уравнение малых колебаний плавающей вязко-упругой ледяной пластины, рассматриваемой как модель Максвелла

Для того чтобы рассмотреть прогиб ледяной пластины под действием движущейся нагрузки, имитируя лед вязко-упругой моделью Максвелла, необходимо в общей модели исключить узел Кельвина, т.е. положить , . Тогда уравнение (2.6) примет вид:

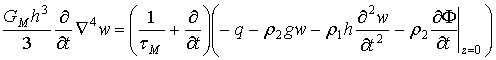(2.22)

Если решать уравнение (2.22) аналогично решению уравнения (2.6), т.е. переходя к системе координат, совмещенной с движущейся нагрузкой, рассматривая стационарный случай и используя преобразование Фурье для функций w, q и F, можно получить следующий результат:

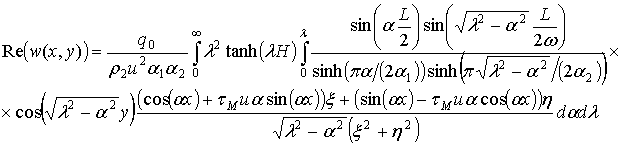
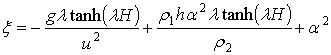(2.23)

.

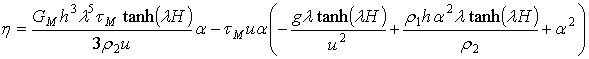Формула (2.23) позволяет вычислить прогиб пластины, если лед рассматривается как вязкоупругое тело по модели Максвелла. Это же самое выражение можно получить, полагая в формуле (2.21) и .

Для нагрузки, распределенной по прямоугольнику, формула для расчета прогиба пластины получается аналогично из (2.19) подстановкойи :

.

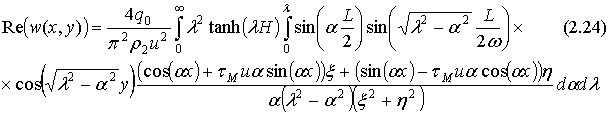Здесь величины x и h вычисляются по формуле (2.23).