Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания

Прикладные задачи динамики ледяного покрова
Козин В. М., Жесткая В. Д., Погорелова А. В., Чижиумов С. Д., Джабраилов М. Р., Морозов В. С., Кустов А. Н.,
2.1.5. Уравнение малых колебаний плавающей вязко-упругой ледяной пластины, рассматриваемой как модель Кельвина-Фойгта
Предположим, что период волновых процессов в ледяном покрове много меньше времени релаксации льда. Тогда, согласно работе [124], для льда принимается закон деформирования линейной упруго запаздывающей среды Кельвина-Фойгта [122].
Исходя из сделанных предположений, линеаризованные граничные условия при z=0 для функции потенциала скорости жидкости![]() , удовлетворяющей уравнению Лапласа
, удовлетворяющей уравнению Лапласа ![]() , запишутся как
, запишутся как
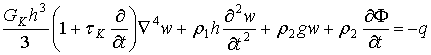 (2.25)
(2.25)
Если совместить новую систему координат с движущейся нагрузкой, то в новых координатах в стационаре уравнение (2.25) примет вид
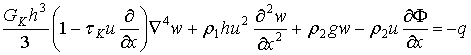 .
.
Данная модель уже рассматривалась в работе [60]. Выражение для прогиба пластины получается аналогично обобщенной модели Кельвина-Максвелла с применением преобразования Фурье (2.11) для основных функций, участвующих в уравнении (2.25) и имеет следующий вид для функции давления (2.20), распределенной по гиперболическому тангенсу:
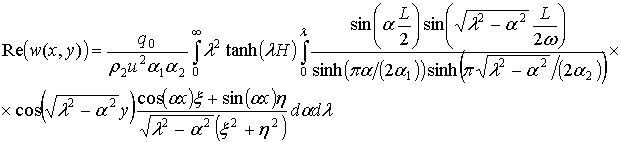
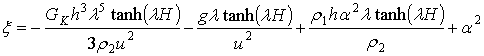 (2.26)
(2.26)