
Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания

Прикладные задачи динамики ледяного покрова
Козин В. М., Жесткая В. Д., Погорелова А. В., Чижиумов С. Д., Джабраилов М. Р., Морозов В. С., Кустов А. Н.,
2.1.6. Численный расчет прогиба пластины
Рассмотрим вычисление прогиба пластины по формулам (2.21), (2.23), (2.26) в программе MathCAD. Для нахождения границ применимости моделей Максвелла и Кельвина-Фойгта будем варьировать времена релаксации ![]() и
и![]() и модули GM и GK от нуля до бесконечности и сравнивать полученные результаты с экспериментальными графиками [158, 160] (Рис.2.6, 2.7).
и модули GM и GK от нуля до бесконечности и сравнивать полученные результаты с экспериментальными графиками [158, 160] (Рис.2.6, 2.7).
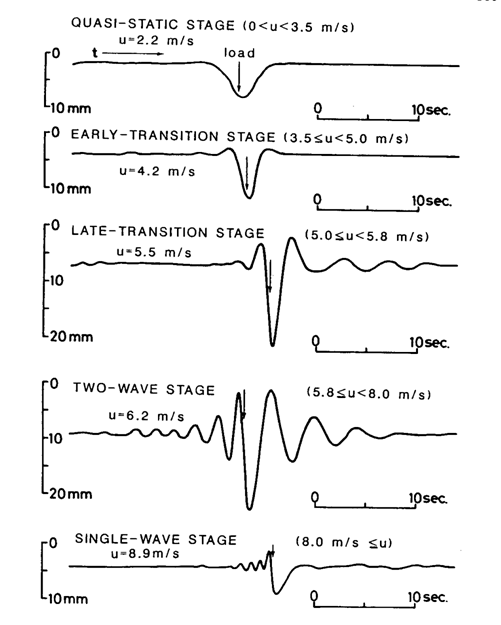
Экспериментальные данные, приведенные на Рис. 2.6, получены для стационарного движения снегохода по ледяному покрову озера для различных скоростей и характеризуют пять различных режимов прогиба льда, предложенных автором:
§ квазистатический режим;
§ ранний переходный режим;
§ скоростной переходный режим;
§ двухволновой режим;
§ «псевдобезнагрузочный» режим.
 .
.
Рис.2.6. Экспериментальные зависимости прогиба ледяной пластины при стационарном движении по ней распределенной нагрузки (взято из [160]).
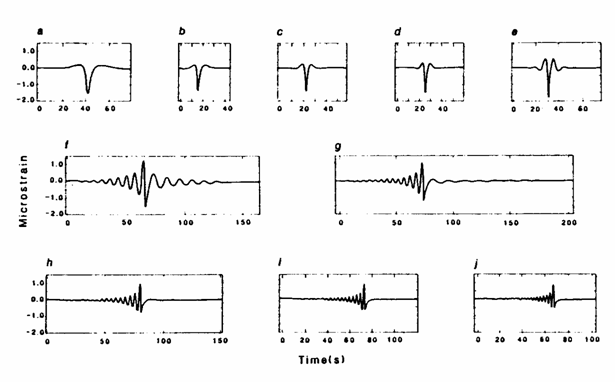
Экспериментальные данные, изображенные на Рис. 2.7 получены в результате эксперимента Project Kiwi 131 и опубликованы в [158].
Для того, чтобы сравнить полученные теоретические результаты с результатами эксперимента [160], зададимся следующими значениями основных характеристик судна, льда и водоема, взятыми из работы [160]:
![]() ;
; ![]() ;
; ![]() ,
, ![]() , (2.27)
, (2.27)
![]() ;
;![]() ;
;![]() ;
;![]() ;
;![]() ;
;![]() .
.
Из сравнения формул (2.21), (2.23), (2.26), можно сделать вывод, что результаты расчетов по формуле для обобщенной модели (2.21) при ![]() и
и![]() должны совпадать с результатами расчетов по формуле (2.23), т.е. с моделью Максвелла, а при
должны совпадать с результатами расчетов по формуле (2.23), т.е. с моделью Максвелла, а при![]() и
и![]() - с результатами формулы (2.26), т.е. с моделью Кельвина-Фойгта.
- с результатами формулы (2.26), т.е. с моделью Кельвина-Фойгта.
 .
.
Рис. 2.7 Показания тензодатчика в зависимости от времени (взято из [158]); здесь перемещения измеряются в микронах (10-6), а скорости в м/c для следующих значений скорости: (a) 4.5; (b) 8.9; (c) 13.8; (d) 15.7; (f) 18.4; (g) 20.8; (h) 23.2; (i) 25.8, (j) 28.5. Начало отсчета времени произвольно.
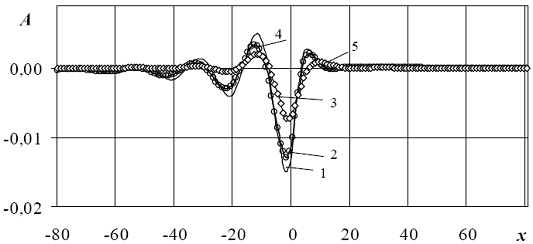
На рис. 2.8 представлено сравнение расчетов по формулам (2.21), (2.23), (2.26) для h= 0.075м, H=6.8м, u=5.5м/с, y=0м. Кривая 1 – обобщенная модель Максвелла-Кельвина при tК=0.34с, tМ=0.34с, , ; кривая 2 – обобщенная модель Максвелла-Кельвина при tК=0с, tМ=0.34с, ![]() ,
, ![]() ; кривая 3 – обобщенная модель Максвелла-Кельвина при tК=0.34с, tМ=0.34с,
; кривая 3 – обобщенная модель Максвелла-Кельвина при tК=0.34с, tМ=0.34с, ![]() ,
, ![]() ; кривая с маркерами 4 – модель Максвелла при tМ=0.34с,
; кривая с маркерами 4 – модель Максвелла при tМ=0.34с,![]() ; кривая с маркерами 5 – модель Кельвина при tК=0.34с,
; кривая с маркерами 5 – модель Кельвина при tК=0.34с, ![]() .
.
 .
.
Рис.2.8 Прогиб пластины при расчете по различным моделям
Из рис.2.8 видно, что если в формуле (2.21) взять![]() ,
, ![]() , то результаты совпадают с результатами формулы (2.23) (обобщенная модель выходит на модель Максвелла). Если в формуле (2.21) взять
, то результаты совпадают с результатами формулы (2.23) (обобщенная модель выходит на модель Максвелла). Если в формуле (2.21) взять ![]() и даже не менять tM, получится, что результаты совпадут с результатами формулы (2.26) (обобщенная модель выходит на модель Кельвина-Фойгта). Таким образом, выход обобщенной модели на простые модели Максвелла и Кельвина-Фойгта имеется и не противоречит физическому смыслу. С другой стороны, если обобщенная модель Максвелла-Кельвина (кривая 1) при рассматриваемых параметрах (tК=0.34с, tМ=0.34с,
и даже не менять tM, получится, что результаты совпадут с результатами формулы (2.26) (обобщенная модель выходит на модель Кельвина-Фойгта). Таким образом, выход обобщенной модели на простые модели Максвелла и Кельвина-Фойгта имеется и не противоречит физическому смыслу. С другой стороны, если обобщенная модель Максвелла-Кельвина (кривая 1) при рассматриваемых параметрах (tК=0.34с, tМ=0.34с,![]() ,
,![]() ) хорошо приближается к эксперименту, то модели Кельвина-Фойгта и Максвелла не дают достаточного прогиба ледового покрова. Поэтому необходимо рассмотреть отдельно линейные модели Максвелла и Кельвина-Фойгта, поварьировать параметры tК, tМ,
) хорошо приближается к эксперименту, то модели Кельвина-Фойгта и Максвелла не дают достаточного прогиба ледового покрова. Поэтому необходимо рассмотреть отдельно линейные модели Максвелла и Кельвина-Фойгта, поварьировать параметры tК, tМ, ![]() ,
,![]() и посмотреть, при каких условиях эти модели совпадают с экспериментальными данными [158, 160], изображенными на рис. 2.6 и 2.7.
и посмотреть, при каких условиях эти модели совпадают с экспериментальными данными [158, 160], изображенными на рис. 2.6 и 2.7.