Научная электронная библиотека

Монографии, изданные в издательстве Российской Академии Естествознания

Прикладные задачи динамики ледяного покрова

Козин В. М., Жесткая В. Д., Погорелова А. В., Чижиумов С. Д., Джабраилов М. Р., Морозов В. С., Кустов А. Н.,

2.1.7. Сравнение теоретических расчетов прогиба ледяной пластины, имитируемой моделью Максвелла с результатами эксперимента

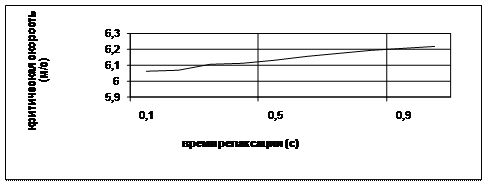
Проведем расчеты по формуле (2.23). Предположим, что в модели Максвелла величина , и будем рассматривать влияние времени релаксации tМ на различные параметры движения и прогиба пластины в условиях эксперимента [160] (2.27). На рис. 2.9 приведена зависимость критической скорости от времени релаксации tМ (здесь и далее будем считать критической скоростью скорость с наибольшим заглублением ледяного покрова w).

.

Рис. 2.9 Влияние времени релаксации по Максвеллу на значение критической скорости

Из рисунка видно, что увеличение вязкостных сил (уменьшение tМ ) приводит к уменьшению критической скорости по сравнению с упругой пластиной. Данный факт согласуется с выводами работ [143,158, 160]. Заметим, что экспериментально было получено [160], что критическая скорость равна .

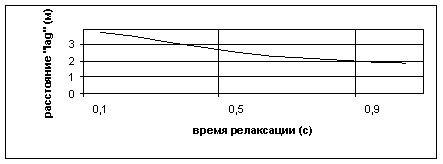
На рис. 2.10 представлена зависимость расстояния от точки максимального прогиба пластины до начала координат для разных значений времени релаксации. В работах [158, 160] данная величина называется “lag”.

Из рисунка видно, что силы вязкости по Максвеллу приводят к увеличению задержки точки максимального прогиба от точки приложения нагрузки. Данный факт также не противоречит физическому смыслу вязкости и с гласуется с результатами работ [158,143].

.

Рис. 2.10 Влияние времени релаксации на задержку прогиба

Экспериментально найденное “lag” в работе [160] лежит в этих же пределах.

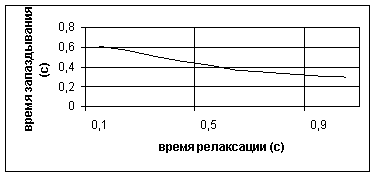
На рис. 2.11 изображено влияние сил вязкости на время запаздывания, т.е. время, которое отделяет момент приложения нагрузки от момента максимального прогиба. В работах [158, 160] эта величина носит название “lag time”.

.

Рис. 2.11 Зависимость времени запаздывания от сил вязкости

Из рисунка видно, что увеличение сил вязкости, т.е. уменьшение времени релаксации tМ приводит к увеличению времени запаздывания. Причем, как и в эксперименте [160], величина времени запаздывания не превышает 0.7с.

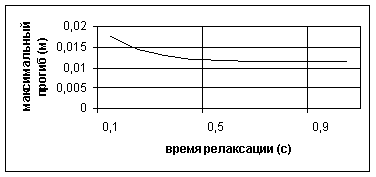
На рис. 2.12 приведена зависимость максимального заглубления ледяной пластины от времени релаксации tМ при критических скоростях движения. Из рисунка видно, что для tМ>0.6c прогиб пластины почти не меняется, а с увеличением сил вязкости tМ<0.5c прогиб пластины растет. Напомним, что в предельном случае, когда , модель вязко-упругого тела по Максвеллу стремится к состоянию, свободному от напряжений, поэтому, с ростом вязкости (уменьшением tМ ) прогиб растет для модели Максвелла. Если в качестве времени релаксации брать величину tМ=0.69с, как предлагается в работах [158, 160], то прогиб пластины немного не дотягивает до экспериментально полученного.

.

Рис. 2.12 Зависимость максимального заглубления ледяной пластины от времени релаксации

Таким образом, полученные теоретические характеристики для чистой модели Максвелла не противоречат физическому смыслу и находят качественное согласование с экспериментальными данными работы [160]. Далее необходимо проверить количественное согласование расчетов по модели Максвелла (2.23) с результатами эксперимента [160]. Будем брать в качестве времени релаксации tМ следующие зависимости:

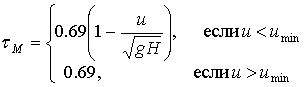, где (2.28)

,

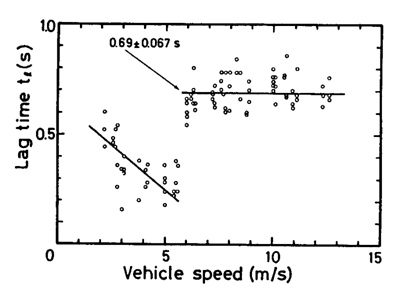
Данные зависимости приведены в [160] в виде экспериментальных точек на Рис. 2.13. Вычисления по формулам (2.28) совпадают с результатами Рис. 2.13.

.

Рис. 2.13. Экспериментальные зависимости времени задержки максимального прогиба пластины «lag time» в зависимости от скорости (from Takizawa, 1985).

Результаты расчетов w по формуле (2.23) с учетом значений (2.27) и (2.28) приведены на рис. 2.14, по оси абсцисс в котором отложено время. Из рисунка видно, что для скорости u=2.2м/c модель Максвелла дает прогиб порядка 10 мм, в эксперименте же он не превышает 7 мм. Для критических скоростей рассчитанный прогиб немного не дотягивает до экспериментальных значений. Но в целом, совпадение с экспериментом хорошее и по качественным, и по количественным характеристикам.