Научная электронная библиотека

Монографии, изданные в издательстве Российской Академии Естествознания

Прикладные задачи динамики ледяного покрова

Козин В. М., Жесткая В. Д., Погорелова А. В., Чижиумов С. Д., Джабраилов М. Р., Морозов В. С., Кустов А. Н.,

2.1.8. Сравнение теоретических расчетов прогиба ледяной пластины, имитируемой моделью Кельвина-Фойгта с результатами эксперимента

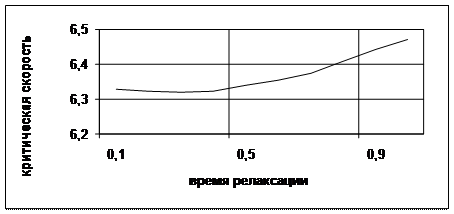
Проведем расчеты по формуле (2.26). Предположим, что в модели Кельвина-Фойгта величина , и будем рассматривать влияние времени релаксации tК на различные параметры движения и прогиба пластины в физических условиях эксперимента [160] (2.27). На рис. 2.15 приведена зависимость критической скорости от времени релаксации tК.

.

Рис.2.14 Расчет прогиба ледяной пластины по модели Максвелла

.

Рис. 2.15 Влияние времени релаксации по Кельвину-Фойгту на значение критической скорости

Из рисунка видно, что увеличение вязкостных сил (увеличение tМ ) приводит к увеличению критической скорости по сравнению с упругой пластиной. Данный факт не согласуется с выводами работ [143,158, 160]. Заметим, что экспериментально было получено [160], что критическая скорость равна .

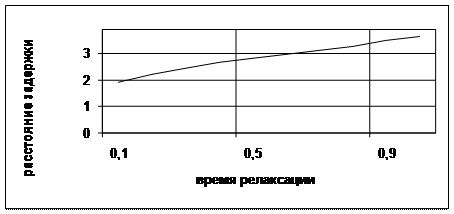
На рис. 2.16 представлена зависимость расстояния от точки максимального прогиба пластины до начала координат (“lag”) для разных значений времени релаксации.

Из рисунка видно, что силы вязкости по Кельвину-Фойгту приводят к увеличению расстояния задержки точки максимального прогиба от точки приложения нагрузки. Данный факт также не противоречит физическому смыслу вязкости и согласуется с результатами работ [158, 143]. Экспериментально найденное “lag” в работе [160] лежит в этих же пределах.

.

Рис. 2.16 Влияние времени релаксации на задержку прогиба

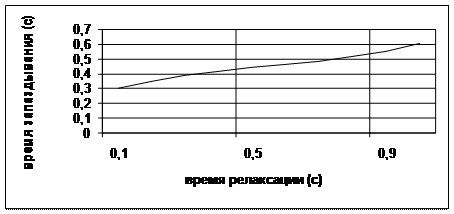
На рис. 2.17 изображено влияние сил вязкости по Кельвину-Фойгту на время запаздывания, т.е. время, которое отделяет момент приложения нагрузки от момента максимального прогиба. В работах [158, 160] эта величина носит название “lag time”.

.

Рис. 2.17 Зависимость времени запаздывания от сил вязкости

Из рисунка видно, что увеличение сил вязкости, т.е. увеличение времени релаксации tК приводит к увеличению времени запаздывания. Причем, как и в эксперименте [160], величина времени запаздывания не превышает 0.7с.

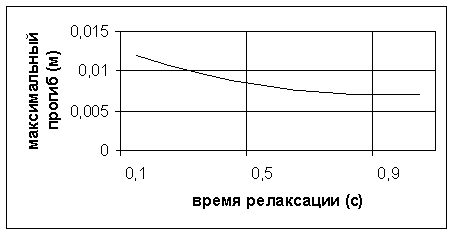
На рис. 2.18 приведена зависимость максимального заглубления ледяной пластины от времени релаксации tК при критических скоростях движения. Из рисунка видно, что для tК>0.8c прогиб пластины почти не меняется, а с уменьшением сил вязкости tК<0.8c прогиб пластины растет. Напомним, что в предельном случае, когда , модель вязко-упругого тела по Кельвину-Фойгту стремится к абсолютно-упругому телу. Если в качестве времени релаксации брать величину tК=0.69с, как предлагается в работах [158, 160], то заглубление пластины намного меньше экспериментально полученного.

.

Рис. 2.18. Зависимость максимального заглубления ледяной пластины от времени релаксации

Таким образом, полученные теоретические характеристики для чистой модели Кельвина-Фойгта не противоречат физическому смыслу и находят качественное согласование с экспериментальными данными работы [160], за исключением влияния вязкости на значение критической скорости. Далее необходимо проверить количественное согласование расчетов по модели

.

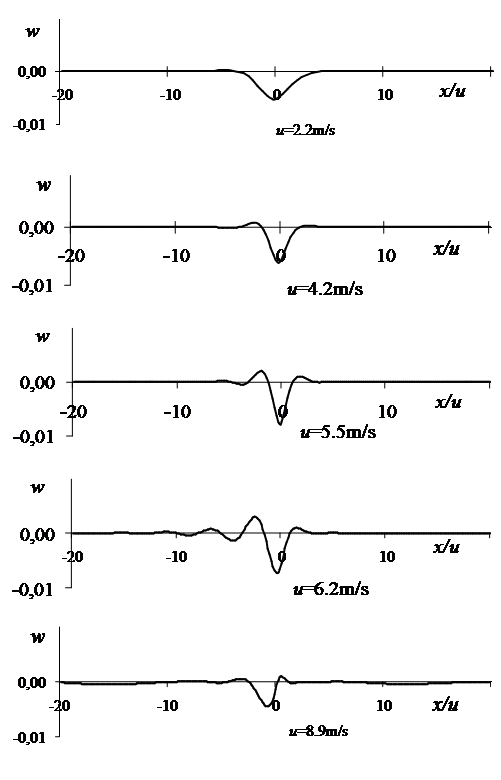
Рис.2.19. Расчет прогиба ледяной пластины по модели Кельвина-Фойгта

Кельвина-Фойгта (2.26) с результатами эксперимента [160]. Будем брать в качестве времени релаксации tК следующие зависимости:

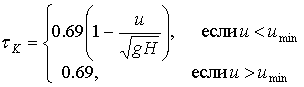(2.29)

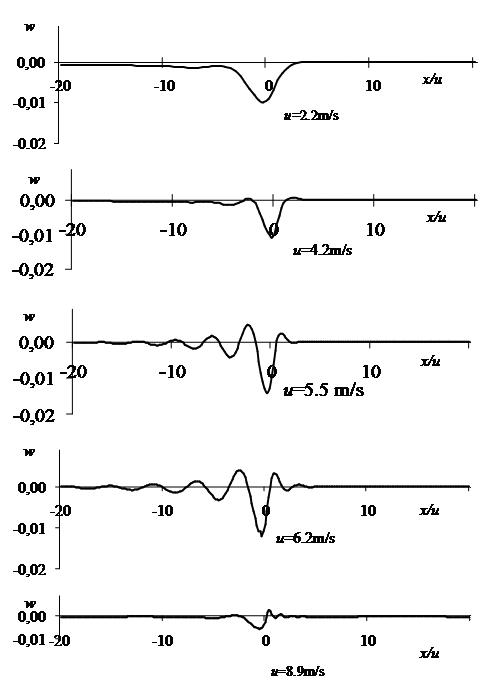
Результаты расчетов w по формуле (2.26) с учетом значений (2.27) и (2.29) приведены на рис. 2.19, по оси абсцисс в котором отложено время. Из рисунка видно, что для малых скоростей u=2.2м/c и u=4.2м/c модель Кельвина-Фойгта дает немного меньший прогиб (на 1-1.5 мм), чем в эксперименте. Для около критических скоростей u=5.5м/c и u=6.2м/c прогиб пластины под нагрузкой недостаточен по амплитуде и плохо сформирована гравитационная волна за нагрузкой. Для сверхкритической скорости изгибная волна перед нагрузкой насчитывает только один горб, хотя в эксперименте и в модели Максвелла этих горбов штуки 4-5.

Таким образом, чистая модель Кельвина-Фойгта хуже приближается к результатам эксперимента, чем чистая модель Максвелла. Однако можно отметить общее в обеих моделях. Во-первых, для обеих моделей наибольший прогиб наблюдается при околокритических скоростях u=5.5м/c и u=6.2м/c; во-вторых, наименьший прогиб – при сверхкритической скорости u=8.9м/c; в-третьих, для малых скоростей u=2.2м/c и u=4.2м/c не наблюдается ни изгибной волны перед нагрузкой, ни гравитационной волны после нее.