Научная электронная библиотека

Монографии, изданные в издательстве Российской Академии Естествознания

Методы повышения эффективности механизированных производственных процессов по условиям их функционирования в растениеводстве: Учебное пособие

Арютов Б. А., Важенин А. Н., Пасин А. В.,

1.3. Анализ существующих методов и критериев оценки эффективности функционирования производственных процессов

Вопросы использования машин в аграрной отрасли определились основоположником земледельческой механики академиком В.П. Горячкиным и профессором Б.А. Линтваревым [48]. Развитие науки об эксплуатации сельскохозяйственных машин значительно продвинули работы Б.С. Свирщевского [49], Г.В. Веденяпина [50], Ю.К. Киртбая [6], М.П. Сергеева [51], С.А. Иофинова [52], В.И. Фортуны [53], Р.Ш. Хабатова [54, 55], В.Д. Саклакова [9], А.Н. Важенина [27], Н.П. Тишанинова [56], А.А. Зангиева [4] и др.[57, 58].

Оптимальному проектированию состава и использования сельскохозяйственных машин в технологических комплексах посвящены труды Э.А. Финна [58], В.Г. Еникеева [59], Б.В. Павлова [40], Р.Ш. Хабатова [54], Б.И. Кашпуры [60], М.В. Шахмаева [61] и др. [3, 63, 64, ..., 70].

Во многих работах уделяется внимание использованию машин при интенсивных и индустриальных технологиях, оптимизации технологических систем и режимов использования машин, прогрессивным поточным и поточно-цикловым методам работы [4, 10, 36, 47, 48, 56, 58, 71, 72, ..., 77].

Разработке и развитию математических методов в исследованиях по оптимизации посвящены работы М.Е. Браславца [79], Б.В. Павлова [40], Э.И. Липковича [7], А.Б. Лурье [79], Р.Ш. Хабатова [54], В.Г. Еникеева [59] и др. [61]. Благодаря их работам были созданы основы моделирования и оптимизации процессов сельскохозяйственного производства.

Вопросам рационального и оптимального построения производственных процессов посвящен целый ряд работ [30, 63, 78, 80, 81, ..., 137].

В настоящее время наступил качественно новый этап по организации рационального использования техники. Применение прогрессивных технологий возделывания сельскохозяйственных культур требует разработки более совершенных методов производственной эксплуатации машинно-тракторного парка и предъявляет повышенные требования к качеству проектирования производственных процессов в сельском хозяйстве.

Указывая на исключительно важную роль проектирования в использовании техники, ряд авторов [26, 138, 139] в то же время отмечает несовершенность традиционных методов. На качество проектирования влияет: использование при расчетах существующей системы усредненных нормативов [30, 32], которые не всегда учитывают особенности данного сельскохозяйственного производства; использование усредненных характеристик по учету природно-климатических условий [34, 35, 38]; использование в расчетах усредненных сроков проведения механизированных работ [39, 140, 141, 142]; формальное отношение в хозяйствах к составлению технологических карт [8, 40] и др.

Обоснование адекватности функционирования технологических систем в растениеводстве погодно-климатическим условиям рассматривается в исследованиях А.Н. Важенина [27], Н.И. Шабанова [144],
И.И. Карманова 145], А.В. Процерова [146], А.Д. Масловской [147],
В.В. Бледных [148], Г.В. Коренева [36] и др. [78, 142, 149, 150, ..., 155].

В настоящее время авторами [156] разработана модель оптимизации состава технологических комплексов машин, реализуемая с помощью пакета прикладных программ ППП ЛПАСУ. Она отличается от других моделей тем, что в качестве критерия оптимизации приняты интегральные затраты. Есть возможность также получить частично целочисленное решение. Моделируемый процесс в типовой программе разбит на рабочие периоды продолжительностью пять дней.

В типовой программе ВНИПТИМЭСХа календарный период описан как переменная продолжительностью от одного до пяти дней.

Для решения типовой оптимизационной задачи использован критерий - минимум приведенных затрат. В сравниваемой с ней модели применялся интегрированный критерий, учитывающий помимо приведенных также и затраты на улучшение социальных и культурно-бытовых условий механизаторских кадров, стоимость потерь урожая от удлинения сроков выполнения отдельных механизированных работ.

В качестве исходной информации в обоих вариантах использованы технико-экономические характеристики машин и агрегатов, тарифные разряды и ставки оплаты механизированных работ, а также ряд других показателей, выбранных в соответствии с существующими нормами и нормативами.

Программа, разработанная во ВНИПТИМЭСХе, позволяет выводить на печать ограниченный перечень выходных форм: оптимальную потребность в энерго- и сельхозмашинах, таблицы распределения тракторов и сельхозмашин по группам назначения, графики загрузки энергомашин и механизаторов по периодам работ, а также график распределения по рабочим периодам машинно-тракторных агрегатов. Кроме того, выходные формы содержат информацию о стоимостных характеристиках выбранного оптимального состава МТП. Программа послеоптимизационного анализа достаточно универсальна и позволяет в дальнейшем увеличивать число форм выходных аналитических документов.

При формировании исходных данных для решения задачи по типовой программе невозможно точно указать сроки начала и окончания работы внутри пятидневки (указывается лишь ее порядковый номер). Это приводит к искажению описания процесса выполнения смежных и взаимосвязанных работ во времени. Используемые в типовой модели алгоритм решения и критерий оптимизации не позволяют минимизировать потребность хозяйства в механизаторах, соизмерять стоимость потерь от незначительного «растягивания» сроков выполнения отдельных работ с дополнительными издержками по увеличению парка машин. Заложенный в рассматриваемую модель принцип постоянства темпа выполнения отдельных работ внутри пятидневки обусловливает появление дополнительных «пиковых» периодов на графиках загрузки машин и механизаторов, ведет к увеличению их потребности.

К недостаткам типовой модели следует отнести также невозможность модельного выбора наилучшей из альтернативных технологий возделывания и уборки сельскохозяйственных культур.

Получившие широкое применение методы целочисленного программирования основываются на решении нецелочисленных задач линейного программирования с последующим движением к целочисленному решению введением дополнительных отсекающих плоскостей и решением задач линейного программирования для математических моделей, включающих дополнительные ограничения.

С учетом того, что общие методы целочисленной оптимизации задач нелинейного программирования разработаны еще не достаточно для практического применения, Т.Р. Хабатовой представлен [157] алгоритм, учитывающий специфику математической модели задачи:

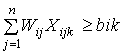;                                     (1.1)

,                                           (1.2)

где 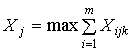- целые числа;

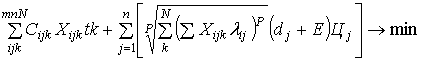,      (1.3)

где  n - число машин;

j, i, k - соответственно индексы машин, видов, работ, календарных периодов;

W - эксплуатационная производительность агрегатов;

X - число машин;

b - объем работ;

т - число видов работ;

N - число календарных периодов;

С - эксплуатационные затраты (без реновации);

t - продолжительность периода;

Р - задаваемая константа, величина которой определяет погрешность a аппроксимации;

λ - число машин в агрегате;

d - отчисления на реновацию;

Е - норма эффективности капиталовложений;

Ц - балансовая стоимость машины.

Анализ математической модели (1.1), (1.2), (1.3) показывает, что она состоит из k задач размерностью тп, связанных вторым слагаемым функции цели. Однако при вычислении ее частных производных по переменным математической модели получаем компоненты градиента, не зависящие от k.

При целочисленной оптимизации надо учесть, что потребность в сельскохозяйственной технике определяется не на всех видах работ и не во всех периодах, а только в тех случаях, когда объем работы максимальный, т.е. следует оптимизировать не Х_ijk, число которых в общем виде составляет mnN, a X_j, которые принимают только m значений.

Поэтому на втором этапе вместо многократного решения задачи для периодов, в которых хотя бы одно из X_j максимально (таких периодов бывает 4-5 из 73), достаточно решить распределительные задачи для вариантов целых чисел X_j. При этом вместо перебора вариантов сочетаний целочисленных значений эффективнее использовать потенциалы X_j, полученные решением обобщенной распределительной задачи методом градиентного движения в пространстве двойственных переменных с применением сглаживающей функции [157].

Задачи управления уборочно-транспортными комплексами представляют практический интерес для тех крупных хозяйств, в которых в период уборки задействованы диспетчерские службы. Модель оптимизации уборочно-транспортного процесса представлена [94] задачей кусочно-линейного программирования, а целевая функция является выпуклой кверху.

Содержательная постановка задачи. С некоторой площади, условно (в зависимости от сроков созревания, качества урожая и удаленности от приемного пункта) разбитой на М участков (1, 2, 3, ..., M) и с известной урожайностью А_i каждого участка (i = 1, 2, 3, ..., M) планируется собрать урожай бригадами К (K = 1, 2, 3, ..., K), каждая из которых работает с известной сменной производительностью W₁, W₂, ..., W_K. Предполагаемые дни уборки (далее сезон) пронумерованы от 1 до N. Таблица С (M, N) размерами М на N указывает на оптимальные сроки уборки урожая. В качестве единицы измерения этой величины взята прибыль (или доход) С_ij, получаемая от единицы продукции, собранной с i-го участка в j-ю смену. Каждая строка С_i = (С_i1, C_i2, ..., С_iN) представляет собой табличные значения некоторой целевой функции Z = С_i(t), в которой каждому временному аргументу t (1:N) соответствует прибыль C_i(t). Известно, что функции Z = С_i(t) - выпуклые кверху.

При таких исходных данных требуется построить некоторый график уборки, т.е. такую таблицу Т (К, N), в которой элемент T_ij - номер того участка, где должна работать i-я бригада в j-й день. Очевидно, что график Т должен удовлетворять следующим требованиям (ограничениям): 1 - за N дней должен быть убран весь урожай; 2 - бригады должны работать без простоев; 3 - прибыль, полученная за сезон, должна быть максимальной.

Однако такая задача не для всех исходных данных М, N, К, А, С, W может иметь допустимое решение Т из-за второго ограничения, из которого следует, что каждая i-я бригада в любой из j-х дней (j = I, 2, ..., N) работает на одном из участков. Такое жесткое требование далее заменяется условием, что бригады могут быть привлечены к уборке не с первого дня, а позднее и освобождены до конца сезона. Формально это значит, что каждая строка матрицы Т может содержать нулевые элементы (простои бригады), но расположенные только в начале и конце строки. Если между ненулевыми элементами строки нет нулей, то строка называется уплотненной. Матрица называется уплотненной, если все ее строки уплотнены.

Задача, в которой по исходным данным М, N, К, А, С, W строится уплотненная таблица, удовлетворяющая первому и третьему условиям, далее называется задачей об оптимальном уплотненном расписании. Эти ограничения также можно формализовать, записать в аналитической форме и сформулировать математическую модель задачи. Для этого достаточно ввести в употребление функцию f_s (х), определенную на множестве {0, 1, 2, ..., М} при S = 1, 2, ..., к:

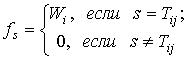.                                   (1.4)

Тогда требование (1.10), что весь урожай должен быть убран за N дней:

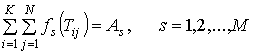,                        (1.5)

а требование о максимальной прибыли, полученной от реализации графика уборки Т:

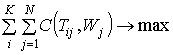.                                  (1.6)

Математическая модель задачи формулируется следующим образом: найти уплотненную матрицу Т(К, N), удовлетворяющую условию (1.4) и максимизирующее значение выражения (1.6).

При каждом выходе из текущего графика (что нередко бывает по погодным условиям или техническим причинам) его можно быстро пересчитать с новыми исходными данными. Подобный оперативный анализ производственной ситуации позволит руководителю оценить отклонение реального уборочного процесса от оптимального и учесть фактические потери.

Описанная модель универсальна и не зависит от размеров и структуры хозяйства и одинаково применима для анализа уборочного процесса как отдельного хозяйства, так и района или региона.

Метод геометрического программирования (ГП) позволяет получить общее решение задачи в виде новой зависимости (двойственной функции) для целевой функции, в которую не входят переменные параметры модели.

Основные особенности и преимущества метода ГП по сравнению с другими методами нелинейного программирования (НЛП) состоят в следующем.

В любой задаче ГП всегда можно получить двойственную функцию для прямой целевой функции, в которую не входят двойственные переменные D, и сначала определяют минимум целевой функции (ее минимизируют) по найденной для нее двойственной функции, а затем переходят к формированию двойственной задачи - нахождению максимума двойственной функции.

Анализируя модели двойственных задач, установлены [158] следующие связи между ними.

Свободные члены ограничений прямой задачи служат коэффициентами целевой функции двойственной задачи, а коэффициенты целевой функции прямой задачи - свободными членами ограничений двойственной. Максимизация (минимизация) целевой функции прямой задачи заменяется минимизацией (максимизацией) целевой функции двойственной задачи.

Каждому ограничению-неравенству прямой задачи соответствует неотрицательная переменная двойственной, а каждому ограничению-равенству - переменная произвольного знака. Каждой неотрицательной переменной прямой задачи соответствует ограничение-неравенство двойственной, а каждой произвольной переменной - ограничение-равенство. В задаче максимизации ограничения-неравенства имеют смысл ≤, в задаче минимизации - ≥.

При формировании двойственной задачи необходимо выполнить условия:

;                                                 (1.7)

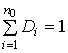;                                              (1.8)

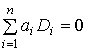,                                              (1.9)

где  n₀ - число переменных в целевой функции;

n - число членов целевой функции;

a_i - любые положительные числа, удовлетворяющие условию ;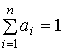

т - число двойственных переменных.

При распределении агрегатов по видам работ в качестве критерия оптимальности может быть принят минимум прямых затрат [40] или расхода топлива. При этом введен ряд ограничений. Одно из них предусматривает обязательное выполнение имеющимся парком заданного объема работ. Однако заранее невозможно определить достаточность ресурсов для выполнения работ в установленные сроки. При нехватке их мы не получим приемлемого решения задачи. В напряженные периоды работ нельзя также допускать излишка ресурсов. Наличие его будет свидетельствовать о возможности дальнейшего сокращения продолжительности выполнения операций.

К тому же в напряженные периоды минимум прямых затрат или расхода топлива на выполнение работ не может служить критерием оптимальности распределения агрегатов. В данном случае наиболее объективный критерий - минимум продолжительности выполнения операций, так как удлинение сроков работ может привести к огромным убыткам из-за потерь части урожая. Поэтому существующая методика распределения агрегатов по видам работ с минимизацией прямых затрат (расхода топлива) может быть применена, на наш взгляд, лишь в ненапряженные периоды, когда операции могут быть выполнены в агротехнические сроки с использованием только части парка. В этой связи разработана [159, 160] математическая модель задачи распределения агрегатов по операциям с минимизацией сроков выполнения работ. Она позволяет получить решение задачи как при нехватке, так и избытке ресурсов. Универсальность модели достигнута благодаря замене условия обязательного выполнения заданного объема работ в периодах требованием выполнения одинаковой доли всех операций:

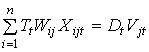,                                   (1.10)

где  T_t - продолжительность t-го периода, дни;

W_ij - дневная производительность агрегата с трактором i-и марки (в дальнейшем i-го агрегата) на j-й операции, га, т;

X_ijt - искомое число агрегатов i-го типа, выполняющих j-ю операцию в t-м расчетном периоде, шт.;

D_t - доля операций в t-м периоде, которая может быть выполнена имеющимся парком;

V_jt - объем j-й операции в i-м периоде, га, т.

Расстановку агрегатов по видам работ по описанной методике можно произвести по любому из известных критериев оптимальности. Критерий, обеспечивающий минимум продолжительности выполнения операций или максимум суммы выполненных долей работ в периодах,

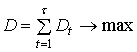.                                    (1.11)

Предложенная модель позволяет решить задачу распределения агрегатов по видам работ как при нехватке, так и избытке ресурсов и определить фактическую продолжительность периодов в обоих случаях.

Использование при этом в качестве критерия оптимальности максимума доли выполненных работ существенно сокращает продолжительность выполнения операций и снижает энергозатраты по сравнению с критериями минимума расхода топлива и прямых затрат. Прямые затраты на выполнение работ при критериях максимума наработки и минимума прямых затрат практически одинаковы. Однако при распределении агрегатов по первому критерию около половины этих затрат компенсируется выручкой от реализации дополнительной продукции, получаемой благодаря сокращению продолжительности операций.

При распределении агрегатов по максимуму наработки существенно сокращается трудоемкость подготовки и ввода в ПЭВМ исходной информации, особенно по сравнению с критерием минимума прямых затрат. При этом отпадает необходимость в трудоемких расчетах прямых затрат на каждой операции по каждому агрегату.

Задачу выбора оптимальных параметров транспортных агрегатов рассмотрим в рамках однокритериальной оптимизации. Критерием оптимизации при этом может быть минимум приведенных затрат. Вариант, обеспечивающий минимальные приведенные затраты, считался наиболее эффективным.

В условиях дефицита ресурсов в каждом конкретном случае могут ставиться и другие цели: снижение капитальных вложений, экономия материальных вложений, материальных затрат (металла, топлива, энергии) и др.

Таким образом, показатель оптимизации часто не удается определить однозначно. В подобных ситуациях необходимо использовать подходы и методы многокритериальной оптимизации. Из всех методов многокритериальной оптимизации наиболее оказался эффективен метод с использованием функции желательности [161]. Удобство ее применения в том, что преобразование частного параметра оптимизации, в показатель желательности d_i включает арифметические действия с матрицами. Применение ПЭВМ при наличии простых программ позволяет быстро производить вычисления по преобразованию функции отклика в функцию желательности, а затем в обобщенную функцию желательности D.

В качестве частных параметров оптимизации при обосновании рациональных параметров применяют эксплуатационные затраты, затраты труда, удельные капиталовложения, материалоемкость, энергоемкость, расход топлива и др.

Однако следует отметить, что функция желательности отдельного показателя есть безразмерное число. Коэффициент желательности

,                                           (1.12)

где  е - основание натурального логарифма;

t - коэффициент, (значение этого коэффициента варьирует от -2,0 до 3,0);

i - индекс показателя.

После преобразования частных параметров оптимизации функций у в соответствующие частные функции желательности d обобщенный показатель

,                                   (1.13)

где р - число частных параметров оптимизации d.

Проблема повышения эффективности использования машин в связи с переходом на рыночные отношения, внедрением механизма самоокупаемости и самофинансирования приобретает особую актуальность, так как прибыль хозяйств и предприятий без государственных дотаций определяется эффективностью использования основных фондов и в первую очередь машин и оборудования.

В работах Дж. Тейлора и В. О. Васильева предложена математическая зависимость для определения рационального срока эксплуатации машин по минимуму затрат средств на единицу выполненной работы или единицу времени за период использования.

По этой методике в настоящее время устанавливают все основные нормативы на эксплуатационные показатели машин (срок службы, длительность межремонтных периодов, нормы производительности и амортизации техники, отчисления на ремонт и др.).

Недостаток методики - показатели использования машин и величина критерия оптимизации представлены функциями лишь одной переменной - возраста машины. Вместе с тем известно, что эти показатели зависят и от других факторов, например, от качества работы машин, их исходных эксплуатационных характеристик, социальных факторов, морального износа, политики ремонта и др.

Важные теоретические и практические результаты [162, 163] получены по новой методике, которая основана на математическом аппарате метода динамического программирования и критерии минимума удельных затрат средств на единицу наработки машины. Она позволяет одновременно учесть многие факторы, влияющие на стратегию эксплуатации машин.

Однако указанная методика оптимизирует процесс эксплуатации машин по локальному оптимуму, т.е. учитывает преимущественно затраты средств в сфере применения техники. В ней не учитываются затраты в машиностроении, металлургии, на транспортирование, хранение, переработку, реализацию продукции, социальные нужды, а также качество работы машин и др.

Динамическая модель оптимизирует стратегию эксплуатации машин этих факторов по совокупному оптимуму. Потери продукции, вызванные снижением качества работы машин, приняты за функцию возраста машины, т.е. по мере старения машины потери продукции возрастают, а цена постоянна.

Значительная часть различных видов ресурсов (материальных, финансовых, трудовых, топливно-энергетических и др.), используемых в сельском хозяйстве, расходуется при работе машинно-тракторных агрегатов (МТА). В связи с этим разработка общих концепций ресурсосберегающего использования МТА имеет актуальное значение. В работе [4] описана общая научная концепция комплексного решения указанной проблемы с позиций системного подхода. Поставленные задачи решаются на целом ряде взаимосвязанных уровней ресурсосбережения (оптимизации) от выбора технологии возделывания сельскохозяйственных культур до частных режимов функционирования отдельных агрегатов.

Трудами Б.А. Линтварева, Б.С. Свирщевского и их последователей Г.В. Веденяпина, М.П. Сергеева, Ю.К. Киртбая, С.А. Иофинова и других ученых созданы теоретические основы использования техники в сельском хозяйстве. Однако они в основном ориентированы на использование машин в крупных коллективных хозяйствах, недостаточно освещают проблемы технической эксплуатации, не учитывают коренные изменения, которые происходят в социально-экономической сфере, в области организации и управления сельскохозяйственным производством. Эти изменения обусловлены формированием свободных товаропроизводителей, выведением большей части предприятий из-под государственной опеки. Кроме того, они требуют совершенствования и развития теоретических основ использования сельскохозяйственной техники с учетом достижений научно-технического прогресса в этой области знаний.

По заданию Россельхозакадемии в ГОСНИТИ с участием ведущих ученых ВИИТиНа, ВИМа, НИПТИМЭСХа, ВНИИМЖа и других институтов разработана концепция эффективного применения сельскохозяйственной техники в условиях рынка [1], которая прошла широкую апробацию и одобрена специалистами.

Концепция базируется на следующих положениях:

• системность рассмотрения проблемы «Человек - машина - среда». Эффективность использования техники зависит в основном от трех взаимосвязанных факторов: качества и надежности техники, качества производственной и технической эксплуатации машин и природно-климатических условий их применения;
• динамичность рассматриваемых факторов. Использование техники рассматривается как сложная динамическая система с большим числом взаимосвязанных и взаимодействующих факторов (техническое состояние машин и оборудования, условия использования техники, состояние работающего с нею персонала и др.);
• многоуровневость системы обеспечения эффективности использования машин и оборудования, состоящей из ряда подсистем, подчиненных общей цели функционирования системы.

Принятая концепция наилучшим образом отражает проблемную ситуацию - недостаточность знаний о рациональном использовании техники в складывающихся условиях ее функционирования.