Научная электронная библиотека

Монографии, изданные в издательстве Российской Академии Естествознания

Методы повышения эффективности механизированных производственных процессов по условиям их функционирования в растениеводстве: Учебное пособие

Арютов Б. А., Важенин А. Н., Пасин А. В.,

2.3. Общая модель производственного процесса в растениеводстве

Производственный процесс в растениеводстве можно рассматривать как многополюсную систему, входы которой представляют собой следующие группы:

Y- технологические входы (семена, химикаты и др.);

R- средства труда (энергетические средства, сельскохозяйственные машины и др.);

L- живой труд (люди, участвующие в производстве).

Выходом V производственного процесса является готовая продукция растениеводства. Производственная функция при этом:

.

Вид этой зависимости может быть разнообразным. В реальном производственном процессе растениеводства каждая группа входов, как и выход, представляют собой многокомпонентные, т.е. векторные величины:

.

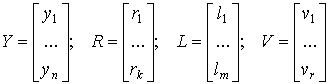Введем в рассмотрение коэффициенты

,

определяющие размер затрат i ресурсов Y, L или R на производство единицы j продукта. Совокупности этих коэффициентов удобно представить в виде следующих матриц:  - материальных затрат;  - трудовых затрат;  - производственных мощностей.

При этом производственная функция может быть записана в виде трех матричных соотношений:

.

Данная модель раскрывает структуру производственного процесса, но не учитывает цели производства - достижение максимальной прибыли.

Повышение эффективности производственного процесса растениеводства состоит прежде всего в достижении оптимального баланса между производством и потреблением, что выражается в составлении балансовых уравнений, описывающих многопродуктовые модели производства. Такие модели могут быть статическими или динамическими.

Статические модели не отражают важнейшего фактора производства, его непрерывного развития и усовершенствования, т.к. рассматривают производственный процесс неизменным на протяжении длительного времени.

Поэтому остановимся на динамической модели.

Внутренними силами, обуславливающими развитие производства, являются капитальные вложения. Последние создаются за счет произведенной и реализованной продукции V и образуют его накапливаемую часть - фонд накопления. Остальная часть составляет фонд потребления.

Фонд накопления можно условно разбить на две части. Первая часть H_R составляет производственные фонды, расходуемые на увеличение и усовершенствование средств производства. Вторая часть H_И направлена на повышение информационного потенциала, куда входят капитальные затраты на научно-исследовательские работы.

Воздействие капитальных затрат происходит всегда с запаздыванием относительно момента их вложения. Капитальные затраты на расширение производственных фондов реализуются, как правило, с меньшим запаздыванием, но имеют и меньшую отдачу. Затраты на научно-исследовательские работы реализуются с большим запаздыванием, но обеспечивают непрерывное совершенствование производственного процесса и могут в корне изменить характер производства.

С целью упрощения будем рассматривать единый фонд накопления H и считать, что эффект от капиталовложений реализуется без запаздывания. Обозначим через  интенсивность продукта, идущего в фонд накопления в i производстве. Уравнение для i производства можно записать в виде

.                             (2.2)

Согласно (2.2) производственный продукт  расходуется на потребление с интенсивностью w_i, на производство с интенсивностью y_i и на увеличение производственных фондов с интенсивностью g_i. Обозначая через y_ij интенсивность расходования продукта i на воспроизводство продукта j, а через g_ij интенсивность расходования продукта i на капитальные вложения в производство продукта j, получаем

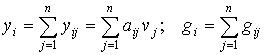.                         (2.3)

Для того, чтобы увязать расход продукта на увеличение производственных фондов с ростом выпуска продукции, необходимо слить воедино два процесса: процесс образования производственного фонда  и процесс его расходования. Рассмотрим приращение производственного фонда  за малый интервал dt. Это приращение пропорционально интенсивности накопления  и интервалу dt:

.                                        (2.4)

Расходование производственных фондов идет на усовершенствование используемых технических средств , поэтому

.                              (2.5)

Сопоставляя (2.4) и (2.5), находим , откуда

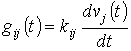,                                         (2.6)

где 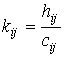 - коэффициент удельных капиталовложений, называемый также коэффициентом капиталоемкости.

С учетом (2.3) и (2.6) уравнения баланса принимают вид

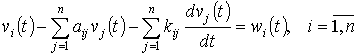.                (2.7)

На основании полученной системы уравнений (2.7) возможна оптимизация производственных процессов растениеводства в среднемноголетних условиях их функционирования (оптимизация стратегии), но адаптация этой модели к изменяющимся погодно-производственным ситуациям требует более детального математического описания.