Научная электронная библиотека

Монографии, изданные в издательстве Российской Академии Естествознания

Прикладные задачи динамики ледяного покрова

Козин В. М., Жесткая В. Д., Погорелова А. В., Чижиумов С. Д., Джабраилов М. Р., Морозов В. С., Кустов А. Н.,

2.1.9. Сравнение теоретических расчетов прогиба ледяной пластины, имитируемой смешанной моделью Максвелла-Кельвина с результатами эксперимента

Проведем расчеты по формуле (2.21). Предположим, что для обобщенной модели Максвелла-Кельвина время релаксации tМ и модуль упругости EМ изменяются по закону:

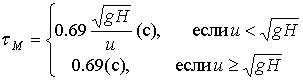, (2.30)

,

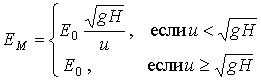где - есть число Юнга для изотропной, гомогенной упругой пластины.

Кроме того, необходимо отметить, что численные расчеты для обобщенной модели Максвелла-Кельвина показали, что в узле Кельвина величины tК и GК взаимосвязаны и дополняют друг друга. А именно, увеличение tК в n раз дает такие же результаты, как и увеличение GК в n раз.

.

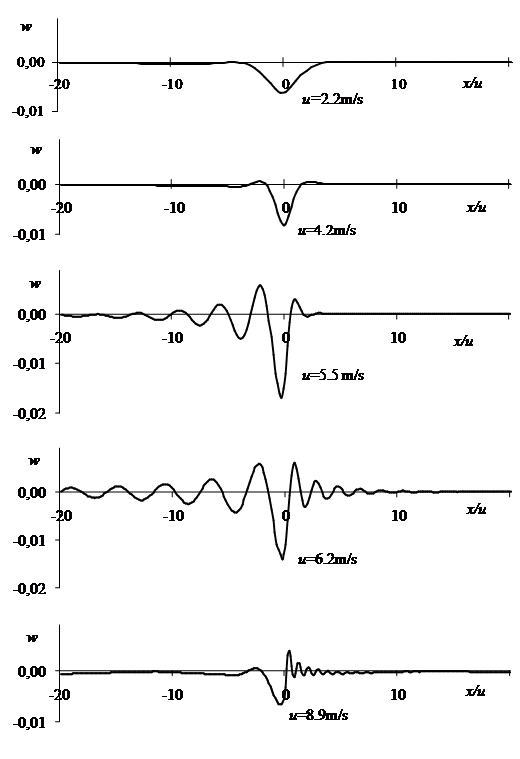
Рис.2.20. Прогиб ледяной пластины для обобщенной модели Максвелла-Кельвина. вычисленный по формуле (2.21) для параметров (2.27), (2.30), (2.31).

Таким образом, достаточно взять одну величину tК, отвечающую за узел Кельвина в обобщенной модели. Наилучшее согласование с экспериментом обобщенной модели имеет место при tК, изменяющемся по закону:

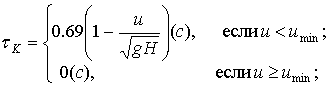
(2.31)

На рис. 2.20 представлены результаты расчета прогиба ледяной пластины по формуле (2.21) для параметров (2.27), (2.30), (2.31).

Данные результаты дают хорошее количественное и качественное согласование с экспериментом [160] (для сравнения смотреть рисунок 2.6). Таким образом, наиболее полно отражают экспериментальные зависимости теоретические результаты, полученные для обобщенной модели вязко-упругого тела Максвелла-Кельвина для параметров вязкости и упругости, рассчитываемых по формулам (2.30) и (2.31).

Для сравнения с экспериментом Project Kiwi 131, представленным в[158], величина деформации вычислялась по приближенной формуле:

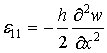(2.32)

На рис. 2.21 представлены зависимости величины деформации в направлении, параллельном движению, расположенные на расстоянии 30м от средней линии движения нагрузки, рассчитанные по формулам (2.21), (2.30)-(2.32) для следующих параметров:

; ; ; ; (2.33)

; ; ; ; ;

; .

Для данных параметров (2.33) величина , а (согласно [124, 158]).

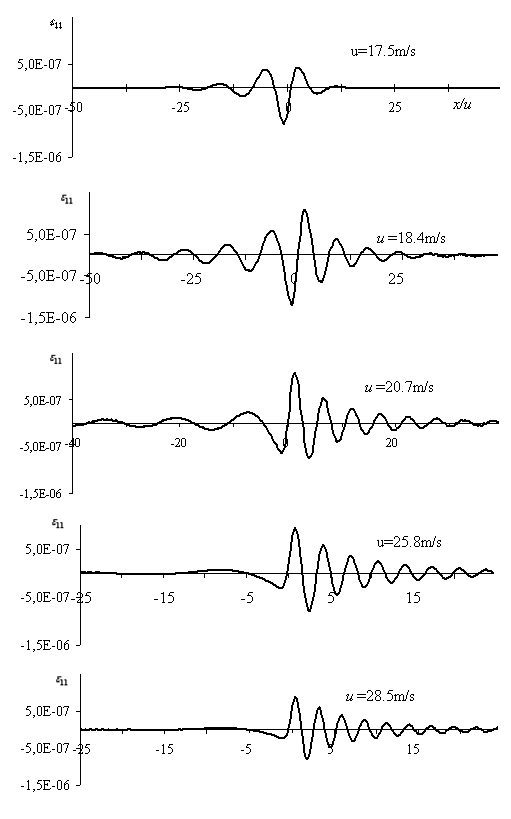
Анализ рисунка 2.21 показывает хорошее качественное согласование результатов обобщенной модели Максвелла-Кельвина с данными эксперимента Project Kiwi 131 [158] (для сравнения смотреть рисунок 2.7).

Необходимо отметить, что расчеты величины деформации по линейным моделям Максвелла или Кельвина (формулы (2.23) и (2.26)) не дают такого качественного совпадения с данными эксперимента Project Kiwi 131 [158], хотя и близки к нему.

Таким образом, для случая движения нагрузки по глубокой воде (при условии ) формулы (2.21) и (2.30), (2.31) дают хорошее совпадение с результатами экспериментов.

.

Рис. 2.21. Микродеформации ледяного покрова, теоретически рассчитанные по формуле (2.21), (2.30)-(2.32) для значений параметров льда и нагрузки (2.33) для сравнения с экспериментом Project Kiwi 131 [158].

Зависимость от скорости u величин tK, tM и EM в формулах (2.30)-(2.31) можно обосновать следующим образом. Для малых докритических скоростей лед приближается к вязко-упругому телу Кельвина-Фойгта . Для сверхкритических скоростей лед приближается к вязко-упругому телу Максвелла с измененным модулем упругости за счет упругих реакций узлов Максвелла и Кельвина . Для околокритических скоростей лед ведет себя как обобщенная четырехпараметрическая модель Максвелла-Кельвина. Численные расчеты показали, что если при критических и сверхкритических скоростях брать , то это приводит к отсутствию в теоретической кривой w изгибной волны перед судном.

Попытаемся зависимости (2.30) и (2.31) распространить на расчеты прогибов реального толстого льда под влиянием движения по льду амфибийного судна на воздушной подушке (СВП) реальных размеров.