Научная электронная библиотека

Монографии, изданные в издательстве Российской Академии Естествознания

Методы повышения эффективности механизированных производственных процессов по условиям их функционирования в растениеводстве: Учебное пособие

Арютов Б. А., Важенин А. Н., Пасин А. В.,

3.2. Функции роста сельскохозяйственных культур в оптимизации производственных процессов

Моделированию роста растений посвящено множество научно-исследовательских работ [227 и др.]. Их назначение - связав временные ряды данных, относящихся к росту организма, в рамках единого математического выражения обеспечить прогнозирование поведения растений. Модели роста растений, построенные следящими методами прогнозирования, могут быть положены в основу оптимизации производственных процессов растениеводства, что обуславливается адекватностью развития сельскохозяйственных культур во времени ситуационному использованию техники при производстве полевых работ [27 и др.].

При решении научно-исследовательских задач традиционен подход - разработка сложной модели с последующим ее упрощением. Однако правомерен и другой путь - начинать с простых соотношений, а затем развивать их по мере углубления в существо проблемы.

Функция роста растительного организма связывает в общем виде сухую массу вещества W и время t [227, 228].

.                        (3.5)

Использование функций роста обычно имеет эмпирическую ориентацию: вид выражения  часто подбирают, исходя из предположения, подсказанным характером имеющегося экспериментального материала. Предпочтительно, однако, попытаться выбрать или построить такую функцию, которая отличалась бы определенным биологическим правдоподобием и интерпретируемостью параметров [229], т.е. отображала бы лежащие в основе изучаемого процесса физиологические и биохимические механизмы и ограничения.

Анализ динамики количества сухого вещества W удобно начинать с обсуждения вопроса о темпах роста, т.е. о производной . Дифференцируя выражение (3.5) по времени, получаем

.                   (3.6)

Затем, исключая из (3.5) и (3.6) переменную t, приходим к выражению

.                   (3.7)

Уравнение (3.7) представляет собой конструкцию: темп есть функция состояния, где в качестве переменной состояния выступает количество сухого вещества W.

Предположим, что в процессе роста преобразование субстрата в сухое вещество происходит без потерь, т.е. система замкнута, поскольку не имеет ни входов, ни выходов.

При допущении, что на рассматриваемом отрезке времени система не получает из внешней среды и не теряет никакого материала, т.е. система со временем приходит в стабильное состояние, справедливо

,                (3.8)

т.к.

.                   (3.9)

где  W₀, S₀ - исходные значения W и S в момент t = 0;

W_f, S_f - значения, к которым приближаются параметры W и S при .

Темп роста представляет функцию

.                                        (3.10)

Поскольку из уравнения (3.9) следует, что , путем подстановки S в уравнение (3.10) получаем

.                             (3.11)

Таким образом, мы пришли к задаче с одной переменной, т.е. теоретически подтвердили гипотезу (3.7).

В реальных условиях функция (3.7) содержит разрывы, не поддающиеся сглаживанию. Причиной может быть резкое изменение режима питания, условий окружающей среды или заболевание.

Сельскохозяйственные системы - комбинации генетических характеристик биологических объектов и условий окружающей среды, среди которых важнейшая роль принадлежит погоде. Известно, что климат (средняя погода) определяет типы культур, выращиваемых в данном регионе, а фактическая погода в течение сезона - функцию роста этих культур. Количественная зависимость между погодой и функцией роста интересна при оптимизации производственных процессов в растениеводстве.

Функция роста при постановке такой задачи в общем виде может быть представлена в форме

,                               (3.12)

где  Р - множество параметров или постоянных коэффициентов, характеризующих организм;

Е_М - параметры либо переменные, характеризующие те условия окружающей среды, которые поддаются управлению;

Е_W - неуправляемые показатели, описывающие погоду (температура, количество осадков и т.д.).

Общеизвестно, что определяющими факторами роста сельскохозяйственных культур являются: свет g_t, тепло T_t, влага r_t, питание S. Из четырех важнейших факторов только , а . Однако при неуправляемости g_t, T_t, r_t прогнозируются с определенной заблаговременностью и приемлемой оправдываемостью и поддаются аппроксимации. По мнению [227 и др.] наиболее приемлемо синусоидальное описание

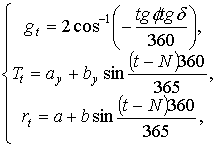                             (3.13)

где   - широта местности, ⁰;

 - угол в момент t между линией, соединяющей солнце и землю и плоскостью экватора, ⁰;

 - среднегодовая температура и амплитуда соответственно, ⁰С;

N - фаза аппроксимирующей синусоиды;

a , b - параметры влагообеспеченности, имеющие тот же математический смысл, что и a_y, b_y , мм..

Субстрат S включает в себя элементы различного происхождения. В частности сухое вещество W может частично разлагаться и повторно синтезироваться. Функция превращения при этом имеет вид

,                                           (3.14)

где  W_n - неразлагаемый компонент;

W_d - разлагаемый компонент.

Почва сама по себе может содержать некоторое количество питательного вещества X_S вне зависимости от того, какое количество X_a этого вещества будет внесено при подкормке. Предполагается, что собственное X_S, вносимое X_a количества питательного вещества и разлагаемый компонент W_d оказывают на культуру аддитивное действие, т.е. справедливо равенство

.                                       (3.15)

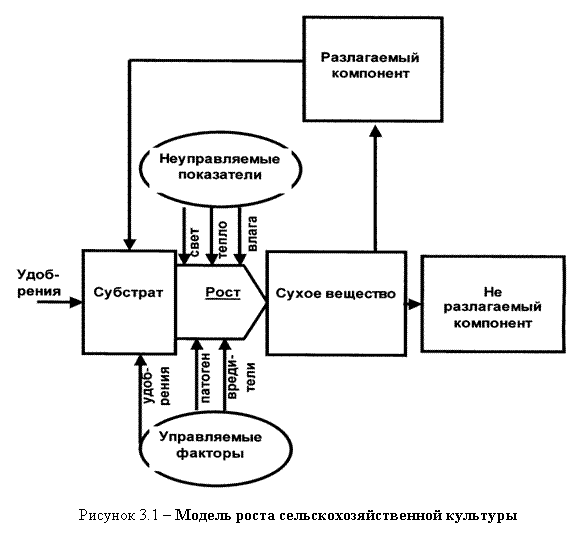
Следует отметить, что содержание вещества в почве X_S и компоненту W_d надо рассматривать и как особенность почвы, и как свойство растения, поскольку определяющее влияние имеет способность корневой системы растения взаимодействовать с почвой и поглащать из нее необходимые питательные элементы, т.е. . Поэтому регулятором субстрата остается  (рис. 3.1).

Пусть норма внесения удобрения i вида составляет X_ai, тогда для данной местности и данного сезона функция отклика может быть представлена в виде

,                              (3.16)

где n - число типов вносимых удобрений.

Норма внесения удобрений, обеспечивающая максимум сухого вещества W, определяется путем приравнивания нулю частных производных функции (3.16):

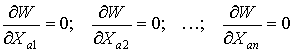.                       (3.17)

Решение этих n уравнений дает набор численных значений , соответствующей в рамках принятых допущений .

Проведенные рассуждения позволяют дополнить двухкомпонентную модель роста.

В схему управления модели роста включены также параметры влияния патогена X_t и вредителей Y_b связанные с защитой растений. Это объясняется тем, что потери урожая от болезней и вредителей повсеместны и значительны. Меры борьбы с ними в настоящее время носят привентивный характер.

Проблема оценки влияния патогена на рост растений является объектом эмпирического моделирования. Чтобы связать зависимую

переменную Х_h (тяжесть заболевания в стадии j развития растения) целесообразно воспользоваться многоточечной моделью.

С помощью многоточечной модели можно анализировать течение болезни в нескольких точках периода вегетации сельскохозяйственной культуры. Если же возникает необходимость в краткосрочном анализе, то приемлима так называемая модель критической точки, с помощью которой можно оценить влияние болезни на физиологию развивающегося растения в стационарной и критической фазах роста.

Подходы, в основе которых лежат многоточечные модели и модели критической точки, могут быть обобщены в рамках одного выражения вида

,                         (3.18)

где w - весовая функция.

Для описания влияния вредителей на рост растений наиболее приемлемым оказалось уравнение Вольтерра [167], которое позволяет обеспечить моделированию больший реализм и лучше согласовывается с теми или иными специальными ситуациями.

Принимая действие закона больших чисел имеем (согласно [230])

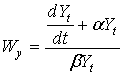,                                     (3.19)

где  W_v - количество сухого вещества, уничтоженного вредителями;

Y_t - число вредителей;

α, β - параметры уравнения.

Стационарное решение может быть получено путем приравнивания  нулю:

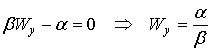.                           (3.20)

Таким образом теоретически обосновали возможность прогнозирования функции роста растения, которая может быть положена в основу оптимизации технико-технологических параметров производственных процессов в растениеводстве.

Для того, чтобы записать уравнение (3.12) в явном виде, необходимо провести эксперимент, в ходе которого изменялись бы условия окружающей среды. Подстановка измеренных погодных показателей совместно с параметрами, характеризующими живой организм, открывает возможность для решения уравнения (3.12), по крайней мере численными методами. Что касается адекватности модели, то она может быть оценена обычным путем - сопоставлением прогнозируемых и фактических данных.