
Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
3.3. Влияние агрометеорологических условий на функционирование производственных процессов в растениеводстве
Повышение эффективности механизированного земледелия требует учета агрометеорологических факторов на всех уровнях принятия хозяйственных решений, что объясняется чрезвычайно сильной зависимостью урожайностей сельскохозяйственных культур от почвенно-климатических ресурсов и погодных условий - в основном света, тепла, влаги, питательных элементов. При этом важную роль должно играть умелое использование достижений современной агрометеорологии - прикладной метеорологической дисциплины, которая изучает атмосферные условия в их взаимной связи с объектами земледелия и процессами сельскохозяйственного производства.
В эффективном использовании этой информации заключены большие резервы повышения продуктивности земледелия. Однако пока эта разнообразная информация используется в эксплуатации машинно-тракторного парка недостаточно.
Оценка агрометеорологических условий включает характеристику состояния сельскохозяйственных культур как отражение взаимодействия условий погоды с сельскохозяйственными объектами и процессами. В основу методов оценки положен разработанный видным русским ученым-агрометеорологом П.И. Броуновым [231] принцип сопряженности наблюдений. Суть этого принципа состоит в одновременности наблюдений за состоянием параметров атмосферы и посевов сельскохозяйственных культур и в совместном объяснении результатов наблюдений.
В своем разнообразии все культуры в жизненном цикле имеют четыре характерных периода: довсходовый, вегетативного роста, репродуктивного роста, старение (рис. 3.2). При этом очевидно, что в каждый из четырех периодов различные культуры имеют различную потребность в питании, свето-, тепло-, влагообеспеченности и др.
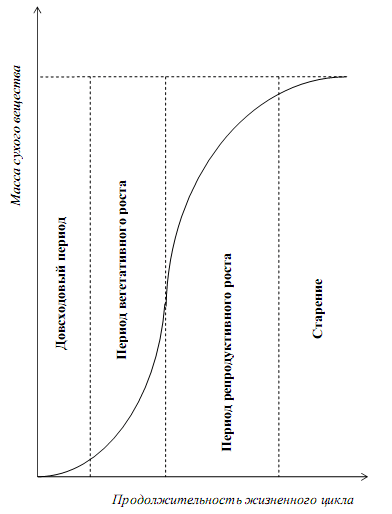
Рисунок 3.2 - Функция роста сельскохозяйственной культуры
На основании статистических данных о сроках наступления природно-климатических и фенологических явлений установлено, что плотности распределения этих случайных величин, как правило, непрерывны, унимодальны и имеют две точки пересечения с осью абсцисс.
Плотность распределения дат наступления группы природно-климатических и фенологических явлений, как правило, имеет незначительную асимметрию, что позволяет их аппроксимировать нормальным (гауссовским) распределением и использовать его свойства для учета сроков работ в технологических операциях по возделыванию культур. Поскольку начало ti любой работы - случайная величина, распределенная по нормальному закону с параметрами mt и ![]() , то можно определить вероятность начала операции в интервале от μ1 до μ2:
, то можно определить вероятность начала операции в интервале от μ1 до μ2:
![]() ,
,
где F(t) - функция распределения случайной величины t с параметрами mt и ![]() через нормальную функцию Ф (t).
через нормальную функцию Ф (t).
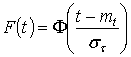 .
.
Вероятность появления случайной величины t в интервале от μ1 до μ2 :
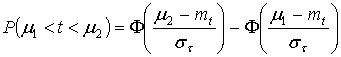 .
.
Следовательно, как при симметричном, так и несимметричном интервалах рассеивания относительно центра повышение его значения увеличивает вероятность начала работы в градациях μ1 до μ2 .
Таким образом, по отдельной работе или комплексу взаимосвязанных работ при неизвестном математическом ожидании mt даты начала работы и среднем квадратическом отклонении ![]() возможна оценка вероятности начала технологических операций в конкретном временном интервале и, следовательно, компенсация влияния неопределенности при установлении потребности в технологических средствах.
возможна оценка вероятности начала технологических операций в конкретном временном интервале и, следовательно, компенсация влияния неопределенности при установлении потребности в технологических средствах.
Существенной является и возможность установления допускаемых значений значений отклонений сроков начала работ от директивных (с учетом которых в детерминированной постановке проводятся оптимизированные расчеты по определению потребности в технике) при принятой вероятности начала работ в интервале от μ1 до μ2 . Однако эта задача может иметь решение только в том случае, если отклонения относительно среднего значения симметричны, т.е.
![]() .
.
При симметричном отклонении ±μ0 относительно среднего значения mt возможной даты начала работы вероятность ее начала в интервале ±μ0 определяется следующим образом. Если интервал от μ1 до μ2 симметричен относительно центра рассеивания и ![]() , а
, а ![]() , то
, то
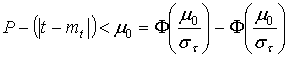 .
.
Поскольку Ф(t) - функция нечетная, то
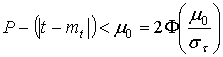 .
.
Таким образом, величину ±μ0 можно определить для любой вероятности ее сохранения при известном среднем квадратическом отклонении ![]() .
.
Анализ статистических характеристик продолжительностей жизненного цикла отдельных сельскохозяйственных культур свидетельствует о наличии в их плотностях распределения ![]() некоторой левосторонней асимметрии. По существу это явление обуславливается рядом причин, основная из которых - изменение погодных условий. Распределением, раскрывающим вероятностную природу этого явления, является
некоторой левосторонней асимметрии. По существу это явление обуславливается рядом причин, основная из которых - изменение погодных условий. Распределением, раскрывающим вероятностную природу этого явления, является ![]() -распределение. В этом случае помимо учета влияния большого числа случайных факторов, каждый из которых в отдельности оказывает несущественное влияние, необходимо учитывать несколько случайных факторов, воздействие которых велико.
-распределение. В этом случае помимо учета влияния большого числа случайных факторов, каждый из которых в отдельности оказывает несущественное влияние, необходимо учитывать несколько случайных факторов, воздействие которых велико.
Плотность ![]() -распределения
-распределения
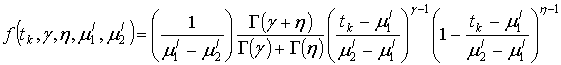 ,
,
где tk - случайная величина;
![]() - параметры формы распределения;
- параметры формы распределения;
![]() - оценки интервала случайных величин;
- оценки интервала случайных величин;
![]() - гамма-функции, определяемые в общем случае как
- гамма-функции, определяемые в общем случае как 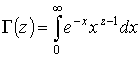 , причем, если z - положительное число, то
, причем, если z - положительное число, то ![]() .
.
В некоторых случаях целесообразно использовать в качестве статистической модели оценки продолжительностей жизненного цикла отдельных сельскохозяйственных культур β-распределение с параметрами
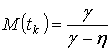 ,
,
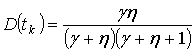 .
.
В целом вид функции плотности ![]() -распределения зависит от показателей
-распределения зависит от показателей ![]() и η. При
и η. При ![]() (и соответственно
(и соответственно ![]() ) функция распределения обращается в ноль в левой (правой) конечной точке вместе с ее первой производной. Для
) функция распределения обращается в ноль в левой (правой) конечной точке вместе с ее первой производной. Для ![]() (и соответственно
(и соответственно ![]() ) кривая имеет вертикальную касательную в левой (правой) конечной точке. Для
) кривая имеет вертикальную касательную в левой (правой) конечной точке. Для ![]() (и соответственно
(и соответственно ![]() ) функция уходит в бесконечность, если значение tk соответствует левой (правой) конечной точке. Для
) функция уходит в бесконечность, если значение tk соответствует левой (правой) конечной точке. Для ![]() и
и ![]() интеграл соответственно равен бесконечности, так что функция распределения перестает существовать. Параметры
интеграл соответственно равен бесконечности, так что функция распределения перестает существовать. Параметры ![]() и η β-распределения:
и η β-распределения:
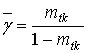 ,
,
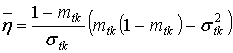 ,
,
где 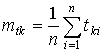 ;
;
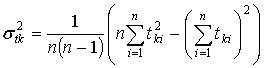 .
.
Возможность оценки левосторонней асимметрии плотности распределения ![]() делает β-распределение приемлемым для формализованного описания продолжительностей жизненного цикла отдельных сельскохозяйственных культур.
делает β-распределение приемлемым для формализованного описания продолжительностей жизненного цикла отдельных сельскохозяйственных культур.
Гипотеза, состоящая в том, периоды полевых механизированных работ пропорциональны соответствующим продолжительностям продолжительностей жизненного цикла отдельных сельскохозяйственных культур, нашла подтверждение на практике.
В практике планирования временных характеристик продолжительностей работ обычно определяют наиболее вероятное время выполнения операции, которое соответствует агротехническим требованиям. Однако из-за различных причин эта оценка продолжительности не выдерживается и, как правило, время выполнения работы увеличивается, т.е. происходит смещение сроков завершения как отдельной операции, так и комплекса работ к более поздним датам.
Отмеченное подтверждено рядом экспериментальных данных по различным группам работ. Таким образом, продолжительность любой работы или комплекса работ, выполняемых последовательно или одновременно, в конкретных временных интервалах делает возможным использование ![]() и β-распределения в качестве типового априорного.
и β-распределения в качестве типового априорного.
Комплексная оценка продолжительностей работ и получение их статистических характеристик возможны в результате статистической обработки данных, собранных в хозяйствах с одинаковой специализацией, и путем экспертных оценок. В случае использования экспертных оценок с учетом априорного времени продолжительностей работ, подчиняющихся β-распределению, оценки статистических характеристик будут определяться следующим образом. Если получены три экспертные оценки продолжительности: tmin- минимальная оптимистическая, tнв- наиболее вероятная и tmax- максимальная пессимистическая, то ожидаемое среднее значение продолжительности работы
![]() ,
,
дисперсия
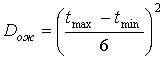 .
.
В случае двух экспертных оценок ожидаемое среднее время
![]() ,
,
дисперсия
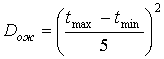 .
.
Экспериментальные данные по оценке продолжительностей механизированных работ позволяют установить возможность аппроксимации этих временных оценок логарифмически нормальным законом распределения, плотность распределения которого имеет вид
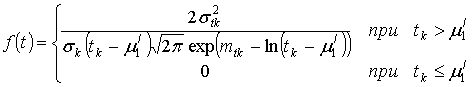 .
.
Данное выражение характеризует плотность распределения случайной величины tk при условии, что случайная величина ![]() распределена по нормальному закону со средним mtk и дисперсией
распределена по нормальному закону со средним mtk и дисперсией ![]() . Основные параметры этого распределения следующие:
. Основные параметры этого распределения следующие:
![]() ,
,
математическое ожидание
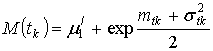 ,
,
дисперсия
![]() .
.
В случае данного вида распределения mtk и ![]() являются параметрами, характеризующими центр распределения и его масштаб.
являются параметрами, характеризующими центр распределения и его масштаб.
Статистический анализ оценок времени технологических операций позволяет установить, что для ![]() и
и ![]() экспериментальные плотности распределения продолжительностей работ могут аппроксимироваться при tk>a распределением вида
экспериментальные плотности распределения продолжительностей работ могут аппроксимироваться при tk>a распределением вида
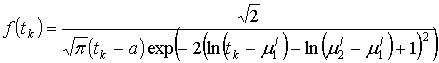
и могут, следовательно, задаваться двумя продолжительностями: ![]() - наименьшей из оценок (оптимистической) и
- наименьшей из оценок (оптимистической) и ![]() - наибольшей из оценок (пессимистической). Графическая характеристика плотности логарифмически нормального распределения в данном случае также унимодальна и положительно асимметрична, так как в нашем случае имеет место правосторонняя асимметрия, которая повышается с увеличением
- наибольшей из оценок (пессимистической). Графическая характеристика плотности логарифмически нормального распределения в данном случае также унимодальна и положительно асимметрична, так как в нашем случае имеет место правосторонняя асимметрия, которая повышается с увеличением ![]() , причем
, причем
 .
.
Таким образом, обработка экспериментальных данных, связанных с характеристиками фенологических фаз развития сельскохозяйственных культур, позволяет установить непрерывный унимодальный характер вероятности плотности их распределения, имеющий две неотрицательные точки пересечения с осью абсцисс, что является общим для установленных видов распределения временных характеристик. При этом плотность распределения фенологических фаз в основном является симметричной и хорошо аппроксимируется гауссовским нормальным распределением. Что же касается продолжительностей проведения механизированных работ, то в силу левосторонней асимметрии их плотности распределения вероятностей наиболее приемлемым является использование β-распределения, позволяющее учитывать как левостороннюю, так и правостороннюю асимметрию и, таким образом, служить вероятностной моделью оценки неопределенности в продолжительностях проведения механизированных полевых работ.
С целью выявления зависимостей продолжительностей периодов цикла жизни сельскохозяйственных культур от агрометеорологических факторов нами проведен регрессионный анализ ретроспективного материала метеостанции «Ройка».
Указанная метеостанция расположена в центральной части Волго-Вятского района и потому характеризует типичные для востока Нечерноземной зоны агрометеорологические условия.
Почвы зоны характеризуются невысоким естественным плодородием. Они бедны необходимыми для сельскохозяйственных растений питательными веществами, и в первую очередь азотистыми соединениями. Содержание в почвах гумуса колеблется от 2 до 4 %. До 74 % пахотных земель имеют повышенную кислотность и нуждаются в известковании. Среди них 15 - 18 % являются «выпаханными», т.е. снизившими свое плодородие в процессе сельскохозяйственного использования. Такие почвы нуждаются в первоочередном внесении органических удобрений. Средняя мощность созданного обработкой и удобрениями пахотного гумусового слоя составляет 18 - 20 см.
В районе преобладают дерново-подзолистые почвы. Объемная масса преобладающих типов почв 1,0 - 1,3 ![]() , а оптимальная влажность для обработки 13 - 26 %, удельное сопротивление плугов - около 50 кПа.
, а оптимальная влажность для обработки 13 - 26 %, удельное сопротивление плугов - около 50 кПа.
В раойне наблюдается частая смена погодных условий, в результате чего почвы зоны в «спелом» состоянии находятся непродолжительное время, что заставляет проводить наиболее энергоемкие операции в сжатые сроки. При многолетнем значении 558 мм наблюдается значительное и неравномерное по периодам года выпадение осадков, годовое количество колеблется от 400 до 700 мм, достигая в отдельные годы 800 - 900 мм и более [232].
Величина же годового испарения не превышает 250 - 500 мм. Это ведет к переувлажнению многих почв на полях с ровным безуклонным рельефом.
Считая влагообеспеченность в зоне вполне удовлетворительной, необходимо учитывать, что не менее двух раз в десятилетие, в мае и июне, наблюдаются засухи [233].
Структура уравнений регрессии определялась в ходе постепенного их «наращивания» переменными. При разработке структуры уравнений регрессии столкнулись с явлением мультиколлинеарности. Под мультиколлинеарностью понимают взаимосвязь независимых переменных уравнения регрессии.
Оценка метода наименьших квадратов производится формулой
![]() , (3.21)
, (3.21)
где a- вектор оценок параметров;
X- матрица значений независимых переменных;
T- операция траспонирования матрицы;
Y- вектор значений зависимой переменной.
Матрица XTX должна быть обратима, а это означает, что ![]() . Последнее, как известно из матричной алгебры, имеет место только тогда, когда векторы, составляющие матрицу, линейно независимы. Если хотя бы два вектора матрицы X линейно зависимы, то наблюдается мультиколлинеарность,
. Последнее, как известно из матричной алгебры, имеет место только тогда, когда векторы, составляющие матрицу, линейно независимы. Если хотя бы два вектора матрицы X линейно зависимы, то наблюдается мультиколлинеарность, ![]() и оценки по формуле (3.21) найти нельзя.
и оценки по формуле (3.21) найти нельзя.
Для обнаружения мультиколлинеарности находится определитель матрицы XTX. Если определитель близок к нулю, то имеется мультиколлинеарность. Устранение мультиколлинеарности достигается путем пересмотра структуры уравнения регрессии - исключением одной из двух, находящихся во взаимосвязи, переменных.
В результате такого рода исследований получены зависимости, представленные в таблице 3.1, которые могут иметь универсальное практическое применение в проектировании использования техники при производстве полевых механизированных работ, т.к. значения независимых переменных прогнозируются синоптиками.
Таблица 3.1 - Уравнения регрессии
|
Культуры |
Периоды |
Начало периода |
Конец периода |
Продолжительность |
Независимые переменные |
|
1 |
2 |
3 |
4 |
5 |
6 |
|
Яровые зерновые |
Довсходовый |
Возобновление |
Появление |
|
x1- длительность светового дня в начале периода, ч; x2- запас продуктивной влаги в метровом слое почвы на начало периода, мм; |
|
Вегетативный |
Появление всходов яровых |
Начало |
|
x3- средняя за вегетативный период температура воздуха, 0С;
x4- средняя за репродуктивный период температура воздуха, 0С. |
|
|
Репродуктивный |
Начало цветения яровых |
Начало восковой спелости яровых |
|
Продолжение таблицы 3.1
|
1 |
2 |
3 |
4 |
5 |
6 |
|
Озимые зерновые |
Довсходовый |
Начало цветения клевера |
Появление всходов озимых |
|
x5- длительность светового дня в начале периода, ч; x6- запас продуктивной влаги в метровом слое почвы на начало периода, мм; x7- средняя за вегетативный период температура воздуха, 0С; x8- среднее за период количество осадков, мм; |
|
Вегетативный |
Возобновление вегетации озимых |
Начало цветения озимых |
|
||
|
Репродуктивный |
Начало цветения озимых |
Начало восковой спелости озимых |
|
x9- средняя за репродуктивный период температура воздуха, 0С. |
|
|
Картофель |
Довсходовый |
Возобновление вегетации озимых |
Появление всходов картофеля |
|
x10- длительность светового дня в начале периода, ч;
x11- средняя за вегетативный период температура воздуха, 0С. |
|
Вегетативный |
Появление всходов картофеля |
Начало цветения картофеля |
|
Продолжение таблицы 3.1
|
1 |
2 |
3 |
4 |
5 |
6 |
|
Клевер |
Вегетативный |
Возобновление вегетации клевера |
Начало цветения клевера |
|
x12- средняя за вегетативный период температура воздуха, 0С; |
|
Репродуктивный |
Начало цветения клевера |
Начало созревания клевера |
|
x13- средняя за репродуктивный период температура воздуха, 0С. |
|
|
Кукуруза |
До |
Возобновление вегетации озимых |
Появление всходов кукурузы |
|
x14- средняя за период температура воздуха, 0С; x15- среднее за период количество осадков, мм; x16- средняя за вегетативный период температура воздуха, 0С; x17- среднее за период количество осадков, мм. |
|
Вегетативный |
Появление всходов |
Начало цветения кукурузы |
|
В теории множеств оператором L называется отображение
![]() ,
,
в котором множества Y и Z являются множествами функций с элементами y(x) и z(x), так что элементами множества L будут пары ( y(x), z(x)). В этом случае говорят, что оператор L преобразует функцию y(x) в функцию
![]() .
.
Если допустить, что y(x) - одно из уравнений регрессии, представленных в таблице, то при помощи оператора L можно прийти к любому уравнению, связывающему погодно-климатические условия с показателями, необходимыми для расчета уровней функционирования техники в растениеводстве.
Пример 1. При проектировании использования техники требуется уравнение, прогнозирующее начало весенних зерно-посевных работ. По теории подобия [27, 234]
![]() ,
,
где y - входная функция, сутки;
z - выходная функция;
25 - среднемноголетняя продолжительность довсходового периода яровых, сутки;
9 - количество суток от начала возобновления вегетации озимых до посева яровых в среднемноголетних условиях.
Тогда согласно таблице 3.1
![]() .
.
Пример 2. При проектировании использования техники требуется уравнение зависимости коэффициента естественных биологических потерь урожая при посеве яровых зерновых культур от агрометеорологических показателей.
По теории подобия
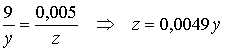 ,
,
где ![]() - коэффициент учета естественных биологических потерь урожая при посеве зерновых культур в среднемноголетних условиях, сут-1.
- коэффициент учета естественных биологических потерь урожая при посеве зерновых культур в среднемноголетних условиях, сут-1.
Тогда согласно таблице 3.1
![]() .
.
Подобных примеров множество.
Таким образом, эмпирические уравнения прогноза фенологических фаз развития сельскохозяйственных культур могут быть положены в основу проектирования технологических процессов растениеводства.
