Научная электронная библиотека

Монографии, изданные в издательстве Российской Академии Естествознания

Прикладные задачи динамики ледяного покрова

Козин В. М., Жесткая В. Д., Погорелова А. В., Чижиумов С. Д., Джабраилов М. Р., Морозов В. С., Кустов А. Н.,

2.1.10. Расчет прогибов реального льда под действием движения СВП при помощи обобщенной модели Максвелла-Кельвина

Анализ натурных испытаний разрушения ледяного покрова [64] судами на воздушной подушке показал, что разрушения льда резонансным методом при помощи СВП происходит, если параметр . Исходя из поставленного условия, для разрушения льда толщиной 1 м необходимо судно длиной не менее 38 м, для льда 0.5 м – не менее 23 м, для льда 1.5 м – не менее 51 м. Таким образом, лед толщиной 0.5м будем «ломать» СВП «Мурена», а лед толщиной 1м и 1.5м – СВП «Зубр», параметры которых представлены в таблице 2.1

Таблица 2.1

Рассмотрим прогиб ледяного покрова, толщиной 0.5м, возникающий в результате движения по ледяному покрову СВП «Мурена» для следующих параметров

; ; , ,(2.34)

; ; ; ; ; .

Для данных параметров льда, судна и водоема верны следующие значения: , т.е. выполняется условие . Следовательно, формулы (2.30)-(2.31) в явном виде работать не могут в области скоростей , так как будут приводить в этой области к отрицательным значениям величины tК. Поэтому перепишем формулы (2.30)-(2.31) в виде:

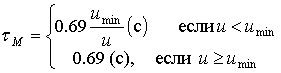(2.35)

;

;

.

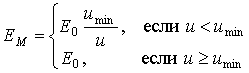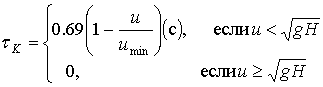Здесь E0 - основной модуль упругости льда (для упругой модели), который зависит от погодных условий и физических свойств льда. Выбор данных зависимостей основан на предположении, что для малой глубины водоема и толстого ледяного покрова критическая скорость нагрузки близка к значению и находится в диапазоне . Формулы (2.35) отличаются от аналогичных (2.30) и (2.31) только тем, что в них величина umin меняется на и наоборот.

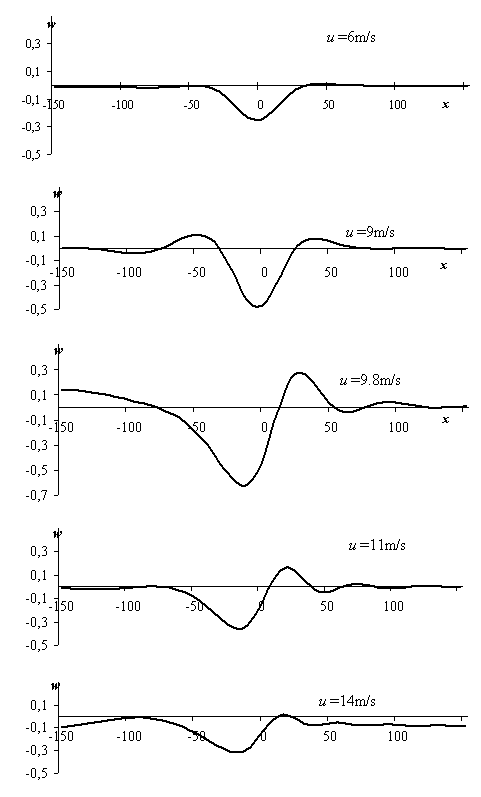
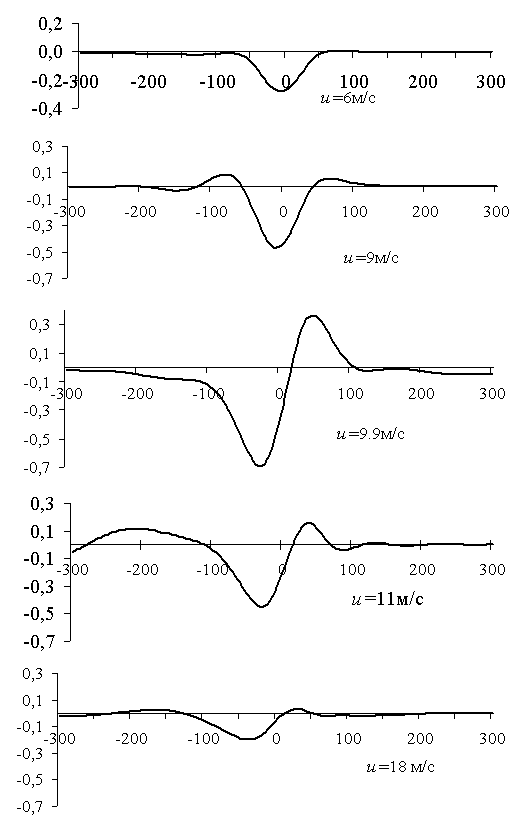
На рис. 2.22 представлены расчеты прогибов ледяного покрова по формуле (2.21) для различных скоростей движения при выполнении условий (2.34)-(2.35), по оси абсцисс отложено расстояние в метрах.

Из рис. 2.22 видно, что наибольший прогиб ледяного покрова наблюдается при движении со скоростью , на этой скорости и следует ожидать вероятного разрушения льда.

На рис. 2.23 представлены результаты расчетов с использованием обобщенной модели Максвелла-Кельвина прогибов ледяного покрова толщиной при движении по нему СВП «Зубр» для водоема глубиной , все остальные параметры (за исключением характеристик судна) совпадают с (2.34)-(2.35). Для рассматриваемого случая . Из рисунка видно, что при движении на малых и сверхкритических скоростях прогиб ледяной пластины мал, а наибольший прогиб ледяного покрова наблюдается при движении СВП со скоростью .

.

Рис. 2.22. Расчет прогибов ледяного покрова с использованием обобщенной модели Максвелла-Кельвина при движении СВП «Мурена» по льду толщиной 0.5м для водоема глубиной 10м

.

Рис. 2.23. Прогиб ледяного покрова толщиной 1м при движении по нему СВП «Зубр» с различными скоростями для водоема глубиной 10м

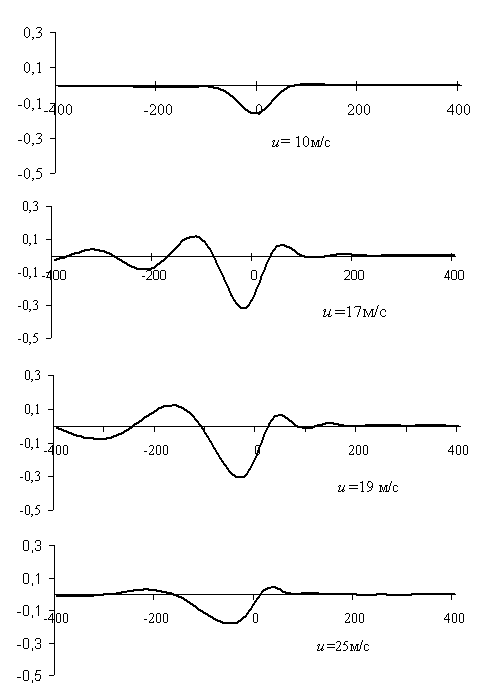
Рис. 2.24. Прогиб ледяного покрова толщиной 1.5м при движении по нему СВП «Зубр» с различными скоростями для водоема глубиной 50м

На рис. 2.24 представлены результаты расчетов с использованием обобщенной модели Максвелла-Кельвина прогибов ледяного покрова толщиной при движении по нему СВП «Зубр» для водоема глубиной , все остальные параметры льда и водоема (за исключением характеристик судна) совпадают с (2.34).

Так как для данного случая (), то в качестве значений времен релаксации и модулей упругости ледяного покрова необходимо брать выражения (2.30)-(2.31). Из рисунка 2.24 видно, что наибольший прогиб ледяного покрова наблюдается при движении СВП с околокритической скоростью . Качественный характер поведения ледяного покрова в зависимости от скорости нагрузки совпадает с экспериментальными данными [160], так как относится к случаю «глубокой воды». В случае же «мелкой» воды (рис. 2.22, 2.23), качественный характер прогибов льда в зависимости от скорости немного иной. Это происходит вследствие того, что для «мелкой» воды выполняется условие и прогиб ледяного покрова с ростом скорости сначала выходит на максимальную амплитуду при скорости за счет гравитационной волны, а потом уже, с дальнейшим ростом скорости, решающую роль начинает играть изгибная волна в ледяной пластине. Конечно же, наибольшей амплитуды стоит ожидать при , но это в реальных условиях почти всегда не выполняется, так как величина umin зависит от толщины льда и не связана с глубиной водоема.

Таким образом, при разрушении льда с помощью СВП на северных реках картина прогиба ледяного покрова будет аналогична рис. 2.22 и рис. 2.23. В данном случае наибольшая амплитуда прогибов наблюдается при . Если же разрушать морской лед при движении по водоему большой глубины, картина прогибов аналогична рис. 2.24 и результатам эксперимента [26] (см. рис. 2.6). При этом наибольшая амплитуда прогибов лежит между величинами и .