
Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
5.5. Оптимизация технической оснащенности механизированных производственных процессов с учетом различных условий их функционирования в растениеводстве
Техническая обеспеченность производственных процессов в растениеводстве определяется условиями их функционирования. Потребность в технике при этом на протяжении ряда лет не является постоянной. В таком случае возникает задача определения стратегии технического оснащения производства.
Решение задачи оптимизации технической оснащенности производственных процессов в растениеводстве с учетом различных условий их функционирования возможно методами теории игр, интенсивно развивающейся математической дисциплины, предметом исследования которой являются методы принятия решений в конфликтных ситуациях.
Специфическим видом игр, имеющих большое значение при анализе различных практических ситуаций, являются стратегические игры. В основе теории стратегических игр лежит предположение, что интересы двух игроков противоположны. Каждый из игроков стремится так выбрать свою стратегию, чтобы получить для себя наибольшую выгоду и свести до минимума выгоду противника. В таких играх каждый игрок действует активно и стремится по возможности использовать оптимальную стратегию.
Однако в нашем случае один из игроков, природа, оказывается нейтральным, т.е. таким, который не стремится извлечь для себя максимальной выгоды и, следовательно, не стремится обратить в свою пользу ошибки, совершаемые противником. Здесь в понятие «природа» мы вкладываем всю совокупность внешних обстоятельств (изменяющиеся условия функционирования производственных процессов в растениеводстве), в которых приходится принимать решение (оптимизация стратегии технического оснащения производственных процессов в растениеводстве).
Природу нельзя рассматривать как разумного противника, который мог бы использовать ошибки, совершаемые человеком. Другими словами, природа не имеет злого умысла по отношению к человеку. Она просто развивается и действует в соответствии со своими законами и во власти человека обратить эти законы себе на пользу. Если бы человек совершенно точно знал законы природы, он мог бы их использовать с максимальной для себя выгодой. Однако это не так.
Неизбежной платой за попытку получить решение в условиях неполной информации о природе является возможность принятия ошибочных решений. При этом ситуации таковы, что отказаться вообще от принятия какого-либо решения невозможно. К тому же решение отказаться от принятия решения также есть решение, и оно может иметь столь же нежелательные последствия, как и другие решения. Единственный выход из создавшейся ситуации - выработка такой стратегии в отношении принятия решений, которая хотя и не исключает возможность принятия неправильных решений, но сводит к минимуму связанные с этим нежелательные последствия.
Правда, есть еще возможность изучать природу, посредством проведения эксперимента. Теоретически путем проведения неограниченного эксперимента можем сделать свои знания о природе сколь угодно полными и действовать уже в условиях полной определенности. Однако этому мешают два обстоятельства: 1) на проведение эксперимента требуется время, тогда как решение нужно принимать сейчас; 2) эксперимент требует затраты средств, т.е. может стоить дорого - дороже того выигрыша, который дают добавочные знания, полученные в результате эксперимента.
Поэтому важной задачей в игре против «природы» является принятие решения о том, нужно ли проводить эксперимент, а если нужно, то какой, когда его закончить и какие действия предпринять после окончания эксперимента.
Под стратегией природы будем понимать полную совокупность внешних условий, в которых приходится принимать решение. Эту совокупность внешних условий назовем состоянием природы ![]() . В общем случае существует некоторое множество возможных состояний природы
. В общем случае существует некоторое множество возможных состояний природы ![]() , которое называется пространством состояний природы, а элементы
, которое называется пространством состояний природы, а элементы ![]() этого пространства - чистыми стратегиями природы.
этого пространства - чистыми стратегиями природы.
Если бы было известно заранее, какую из своих чистых стратегий применяет природа в каждом конкретном случае, то с уверенностью принимали бы решение на основании полного знания состояния природы. Однако известен только перечень чистых стратегий природы и априорное распределение вероятностей ![]() на пространстве состояний природы Θ (смешанная стратегия природы).
на пространстве состояний природы Θ (смешанная стратегия природы).
Задача состоит в том, чтобы принять какое-либо решение из совокупности решений. Обозначим возможные варианты технического оснащения производственного процесса через ![]() . Каждое из этих действий есть чистая стратегия. Множество
. Каждое из этих действий есть чистая стратегия. Множество ![]() является пространством чистых стратегий.
является пространством чистых стратегий.
Необходимо оценить пространство чистых стратегий. Для этого допускаем, что, принимая решение а, можем потерпеть убыток ![]() , зависящий как от выполняемого действия а, так и от неизвестного состояния природы
, зависящий как от выполняемого действия а, так и от неизвестного состояния природы ![]() . Функция
. Функция ![]() , называемая функцией потерь, должна быть заранее определена для всех возможных комбинаций
, называемая функцией потерь, должна быть заранее определена для всех возможных комбинаций ![]() и
и ![]() , т.е. должна быть задана на прямом произведении множеств
, т.е. должна быть задана на прямом произведении множеств ![]() .
.
Знание функции потерь позволяет предпринять действия, которые являются наилучшими в условиях имеющейся информации о состоянии природы.
Нам известна смешанная стратегия природы, т.е. априорное распределение вероятностей ![]() на пространстве состояний природы Θ. Знание априорного распределения вероятностей позволяет определить средние потери при принятии того или иного действия:
на пространстве состояний природы Θ. Знание априорного распределения вероятностей позволяет определить средние потери при принятии того или иного действия:
![]() .
.
Наилучшим решением будет байесовское действие а*, при котором потери минимальны, т.е.
![]() .
.
Таким образом оказывается возможным решение статистической задачи оптимизации технической оснащенности производственных процессов в растениеводстве с учетом различных условий их функционирования. Здесь не делается попытки уточнить свои знания о действительном состоянии природы путем проведения активного эксперимента, а предполагается использовать накопленные статистические данные о состояниях природы.
В качестве примера проведем оптимизацию технической оснащенности зерно-посевного технологического процесса. Для этого рассчитаем по алгоритму, который представлен структурной схемой рисунка 5.5, его технико-технологические параметры при различных погодно-производственных условиях функционирования. Исходные данные примем соответствующие типичному для центральной части Нижегородской области хозяйству. Функцией потерь могут быть дифференциальные затраты. Состояние природы (погодно-климатические условия) определяется метеорологическими данными за последние 30 лет.
Проведенный машинный эксперимент выявил, что оптимальная потребность в технике изменяется в зависимости от условий ее функционирования при коэффициенте сменности 3 от трех единиц формирований по модели ![]() до четырех. Причем наиболее вероятно (0,9) три единицы.
до четырех. Причем наиболее вероятно (0,9) три единицы.
Таким образом множеству стратегий природы противопоставляется два варианта технической оснащенности зерно-посевной технологической линии. Оказалось, что при одинаковой технической оснащенности в различные годы функция потерь изменяется в зависимости от условий функционирования (рисунок 5.8). Возникает задача принципа выбора своей стратегии: какие значения функции потерь закладывать в статистическую игру?
Одним из возможных принципов выбора стратегии может быть принцип минимакса, который успешно применяют в стратегических играх, когда игра ведется против разумного противника, желающего причинить нам наибольший ущерб. Согласно принципу минимакса выбирается такая смешанная стратегия ![]() , при которой средние потери
, при которой средние потери ![]() будут минимальны при наихудшем состоянии природы
будут минимальны при наихудшем состоянии природы ![]() . Наихудшим случаем будет такое
. Наихудшим случаем будет такое ![]() , когда величина
, когда величина ![]() принимает максимальное значение. Эту величину и нужно минимизировать, т.е. выбирать стратегию
принимает максимальное значение. Эту величину и нужно минимизировать, т.е. выбирать стратегию ![]() , которая обеспечивает условие
, которая обеспечивает условие
![]() .
.
Принимая структуру статистической игры и метод ее решения можно составить расчетную таблицу (таблица 5.4).
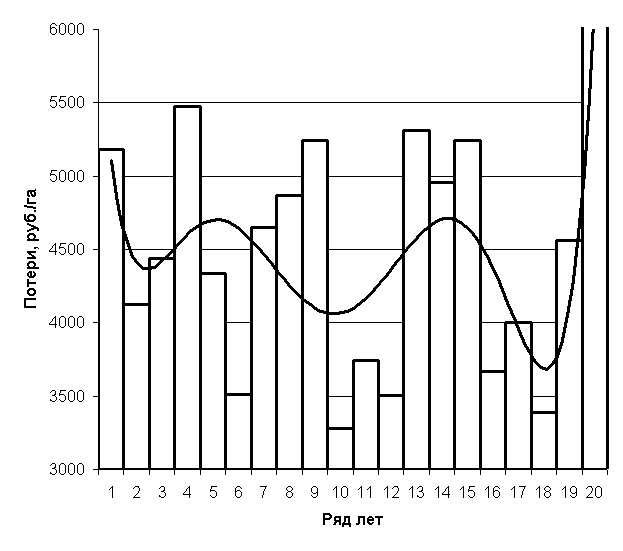
Рисунок 5.8 - Функция потерь в различные по условиям функционирования производственных процессов годы
Таблица 5.4 - Статистическая игра
|
|
|
|
|
|
a1 |
a2 |
||
|
|
0,9 |
5243 |
5738 |
|
|
0,1 |
6825 |
6026 |
Для заданной смешанной стратегии ![]() средние потери при различной технической оснащенности зерно-посевной технологической линии:
средние потери при различной технической оснащенности зерно-посевной технологической линии:
![]() ;
;
![]() .
.
Байесовским будет установление режима а1 - три единицы формирования по модели ![]() , т.е. требуется:
, т.е. требуется:
тракторов: Т-150 - 9;
МТЗ-82 - 6;
сцепок: СП-11 - 9;
сельскохозяйственных машин: МВУ-5 - 3;
КШУ-12 - 3;
ВИП-5,6 - 6;
3ККШ-6 - 6;
СЗА-3,6 - 9.
Предлагаемый метод расчета использовался при разработке нормативов потребности в технике и системы машин в земледелии по агрорайонам Нижегородской области [256].
При сравнении расчетных данных с нормативами [269] потребности в технике по Приволжскому и Уральскому округам обнаруживается отличие на ![]() единицы (в пределе доверительного интервала математического ожидания).
единицы (в пределе доверительного интервала математического ожидания).
