
Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания

Прикладные задачи динамики ледяного покрова
Козин В. М., Жесткая В. Д., Погорелова А. В., Чижиумов С. Д., Джабраилов М. Р., Морозов В. С., Кустов А. Н.,
2.2.2. Волновое сопротивление нагрузки при нестационарном движении по плавающей упругой пластине
Своевременное освобождение рек и морских акваторий ото льда в период межсезонья является важной задачей для народного хозяйства. Для решения этой проблемы как нельзя лучше подходят амфибийные суда на воздушной подушке (СВП). Их большая маневренность, всепроходимость и независимость от глубины акватории позволяет использовать их в тех условиях, где большие ледоколы непригодны. Толщина разрушаемого льда зависит от размеров СВП и его мощности. Проведенные ранее эксперименты [64] показали, что судно «Мурена» длиной 30 м и суммарной мощностью 15000 квт способно разрушать лед толщиной до 0.75 м. и выше было сделано предположение, что десантный корабль «Зубр» длиной 57.3 м в состоянии будет разрушить лед толщиной до полутора метров.
Известно, что при движении СВП по ледяному покрову возникает изгибно-гравитационная волна, которая при резонансных скоростях движения судна достигает своей максимальной амплитуды и при определенных условиях разрушает ледяной покров. Однако работ, посвященных нестационарному движению СВП по сплошному ледяному покрову, очень мало. В статьях [159, 144] рассматривается движение по вязко-упругой пластине нагрузки, описываемой дельта-функцией Дирака по координатам x и y и функцией Хевисайда по времени: ![]() . Данное движение называется зависимым от времени, но мы бы назвали его квазистационарным, так как импульсный рост скорости от нулевого значения до постоянного не в состоянии описывать все возможности нестационарного движения. Рассматриваемая в [159, 144] зависимость может описать безударную посадку самолета на ледяной покров и дальнейшее движение самолета с постоянной скоростью. В работе [103] рассматривалось равнозамедленное движение нагрузки по упругой балке в условиях, что в начальный момент времени нагрузка имеет заданную скорость u и плавно касается балки в заданной точке. Однако, предложенная в [103] функция перемещения нагрузки также не в состоянии описать все возможности нестационарного движения нагрузки по пластине. Поэтому актуальным является рассмотрение нестационарного движения СВП по сплошному ледяному покрову в режимах скоростей, близких к реальным. Известно [109], что волновое сопротивление СВП напрямую связано с прогибом ледяного покрова, образующимся в результате движения СВП и возникновения изгибно-гравитационной волны. Чем больше по амплитуде и углу наклона прогиб ледяного покрова, тем больше волновое сопротивление судна. Поэтому, проанализировав зависимость волнового сопротивления СВП от различных режимов ускорения и торможения, можно сделать выводы о возможности или невозможности разрушения ледяного покрова на том или ином режиме движения.
. Данное движение называется зависимым от времени, но мы бы назвали его квазистационарным, так как импульсный рост скорости от нулевого значения до постоянного не в состоянии описывать все возможности нестационарного движения. Рассматриваемая в [159, 144] зависимость может описать безударную посадку самолета на ледяной покров и дальнейшее движение самолета с постоянной скоростью. В работе [103] рассматривалось равнозамедленное движение нагрузки по упругой балке в условиях, что в начальный момент времени нагрузка имеет заданную скорость u и плавно касается балки в заданной точке. Однако, предложенная в [103] функция перемещения нагрузки также не в состоянии описать все возможности нестационарного движения нагрузки по пластине. Поэтому актуальным является рассмотрение нестационарного движения СВП по сплошному ледяному покрову в режимах скоростей, близких к реальным. Известно [109], что волновое сопротивление СВП напрямую связано с прогибом ледяного покрова, образующимся в результате движения СВП и возникновения изгибно-гравитационной волны. Чем больше по амплитуде и углу наклона прогиб ледяного покрова, тем больше волновое сопротивление судна. Поэтому, проанализировав зависимость волнового сопротивления СВП от различных режимов ускорения и торможения, можно сделать выводы о возможности или невозможности разрушения ледяного покрова на том или ином режиме движения.
Гидродинамическая задача о движущемся по сплошному льду СВП моделируется с помощью системы поверхностных давлений [109], перемещающейся над плавающей ледяной пластиной [124].
Рассмотрим бесконечную область, покрытую сплошным льдом, по которой со скоростью u(t) перемещается заданная система поверхностных давлений q. Совмещенная с судном система координат располагается следующим образом: плоскость xOy совпадает с невозмущенной поверхностью раздела лед – вода, ось x направлена в сторону движения судна, ось z – вертикально вверх. Предполагается, что вода – идеальная несжимаемая жидкость плотности r2, движение жидкости потенциальное. Ледяной покров моделируется упругой, изначально ненапряженной однородной изотропной пластиной.
Согласно [109, 17], величина волнового сопротивления, действующего на СВП, вычисляется по формуле (2.36).
Линеаризованное кинематическое условие на поверхности раздела лед – вода имеет вид
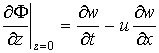 , (2.52)
, (2.52)
где u(t) – скорость системы поверхностных давлений, F(x,y,z,t) - функция потенциала скорости жидкости, удовлетворяющая уравнению Лапласа ![]() .
.
Исходя из сделанных предположений, линеаризованные граничные условия для w(x,y,t) и F(x,y,z,t) запишутся как:
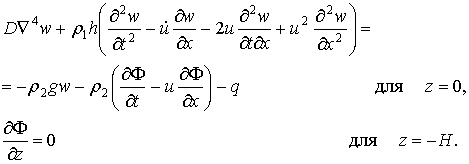 (2.53)
(2.53)
где D – цилиндрическая жесткость ледовой пластины, ![]() ; Е - модуль Юнга, n - коэффициент Пуассона; h(x,y) - толщина льда, r1(x,y) – плотность льда; H=H1-b; H1 – глубина водоема; b=r1h/r2 – глубина погружения льда при статическом равновесии. Для больших глубин, когда H1 намного больше h, можно считать H » H1. В дальнейшем предполагается, что величины r1 и h – постоянные. В качестве расчетных величин D и r1 следует принимать их приведенные значения, определяемые как интегральные величины по толщине пластины.
; Е - модуль Юнга, n - коэффициент Пуассона; h(x,y) - толщина льда, r1(x,y) – плотность льда; H=H1-b; H1 – глубина водоема; b=r1h/r2 – глубина погружения льда при статическом равновесии. Для больших глубин, когда H1 намного больше h, можно считать H » H1. В дальнейшем предполагается, что величины r1 и h – постоянные. В качестве расчетных величин D и r1 следует принимать их приведенные значения, определяемые как интегральные величины по толщине пластины.
При условии, что в момент времени t=0 судно не имеет хода и отсутствуют любые возмущения, кроме статической деформации ледовой пластины, начальные условия для функции F(x,y,z,t) запишутся в виде (2.39).
Для того, чтобы теоретически проанализировать влияние ускорения, торможения и равномерного движения на волновое сопротивление СВП, необходимо задать скорость судна как непрерывную функцию u(t), которая будет убывать, возрастать или оставаться постоянной в зависимости от времени. Задание скорости судна в зависимости от времени с использованием функции гиперболического тангенса (смотреть формулу (2.40)) позволяет моделировать ускорение и торможение судна, а также его равномерное движение [66]. Заметим, что в реальных условиях движения СВП практически невозможно задать скорость судна в точности по закону (2.40), а можно только приблизить его к этому закону своевременными ускорениями или торможениями. Данный закон (2.40) принимается только для математического описания всех возможных режимов движения СВП и теоретического исследования качественных характеристик изменения волнового сопротивления СВП в зависимости от ускорения или торможения судна.
Расстояние, пройденное судном за время t, вычисляется по формуле (2.41).
Предполагается, что в заданной подвижной системе координат давление q не зависит от времени, т.е. q=q(x,y). В качестве системы перемещающихся давлений берется по аналогии с [139, 66] функция (2.42).
Для аналитического решения задачи совершается переход к безразмерной постановке. Для этого вводятся в качестве характерных размеров L – длина судна и u0 – характерная скорость, в качестве которой в дальнейшем выбирается минимальная фазовая скорость![]() [1, 2]. Вводятся безразмерные переменные, функции и параметры:
[1, 2]. Вводятся безразмерные переменные, функции и параметры:
![]()
![]()
![]()
![]()
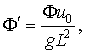
![]()
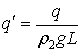 ,
,
 ,
,![]() ,
,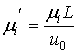 ,
,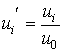 ,
,![]() .
.
(штрихи в дальнейшем будем опускать). Тогда дифференцируя уравнение (2.53) по времени и используя линеаризованное граничное условие (2.52) можно получить безразмерное граничное условие для z=0:
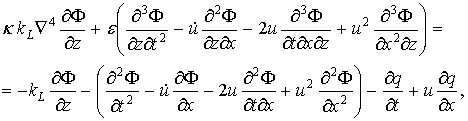 (2.54)
(2.54)
где![]() ,
, ![]() ,
,![]() .
.
Кроме того, следуя [139, 66], предполагается, что функции![]() и
и ![]() удовлетворяют условиям, необходимым для представления их в виде разложения в интегралы Фурье по двум переменным x и y:
удовлетворяют условиям, необходимым для представления их в виде разложения в интегралы Фурье по двум переменным x и y:
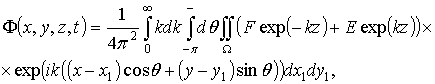
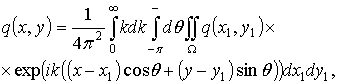 (2.55)
(2.55)
где F и E – неизвестные функции переменных x1, y1, t, k, q. Подстановка выражений (2.55) в граничное условие (2.54) и обезразмеренное граничное условие (2.53) для![]() , где
, где![]() позволяет получить зависимость между величинами F и E:
позволяет получить зависимость между величинами F и E:
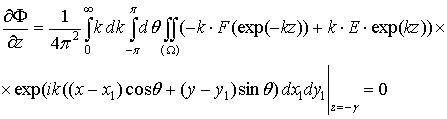
![]()
![]()
![]() (2.56)
(2.56)
Тогда Ф(x,y,z,t) перепишется как:
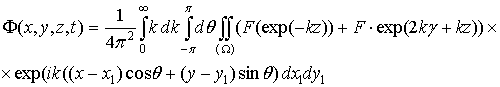 .
.
А значение функции ![]() и всех ее производных в точке z=0 будет иметь вид
и всех ее производных в точке z=0 будет иметь вид
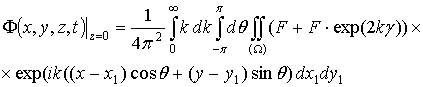
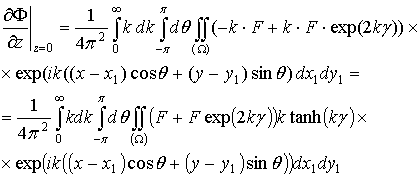
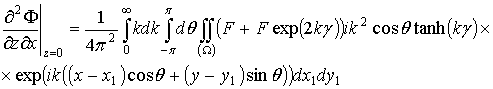
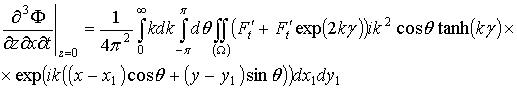
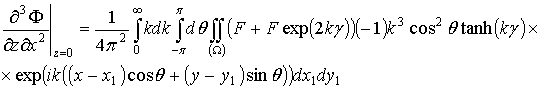
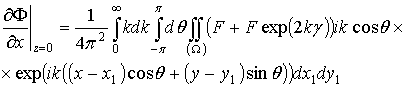
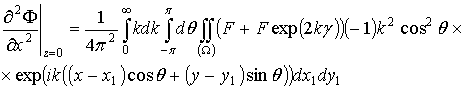
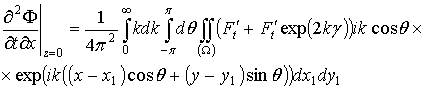
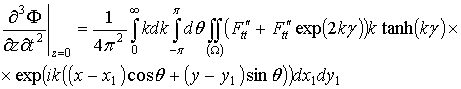
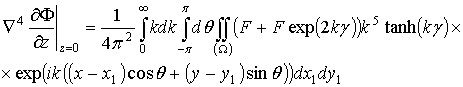
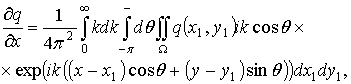 .
.
Подставляя полученные выражения в уравнение (2.54), можно получить следующее выражение для подынтегральных функций:
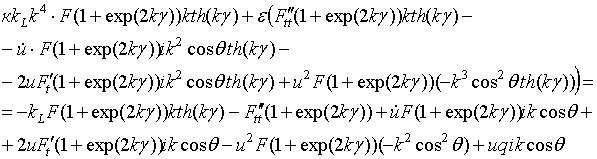 .
.
Деление последнего полученного уравнения на ![]() и использование замены
и использование замены ![]() , дает следующий результат:
, дает следующий результат:
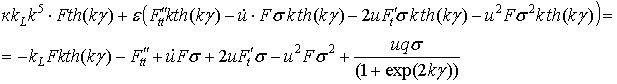 .
.
После приведения подобных членов
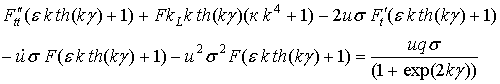 .
.
и деления всего уравнение на ![]() получается следующее линейное неоднородное дифференциальное уравнение второго порядка:
получается следующее линейное неоднородное дифференциальное уравнение второго порядка:
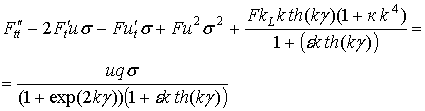 (2.57)
(2.57)
Для решения (2.57) по аналогии с [44, 53] вводится в рассмотрение функция
![]() (2.58)
(2.58)
где s - безразмерное расстояние, пройденное СВП за время t, и вычисляемое по предварительно обезразмеренной формуле (2.41).
Подстановка (2.58) в (2.57) позволяет получить следующие результаты:
![]() ,
,
![]() ,
,
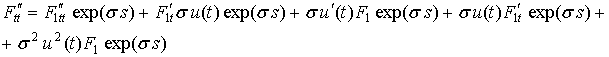
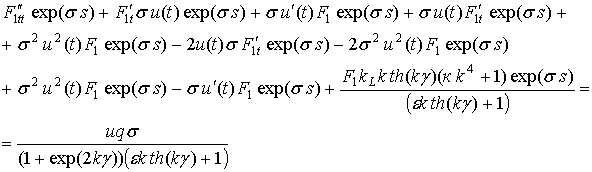 .
.
Приведение подобных членов дает следующее выражение:
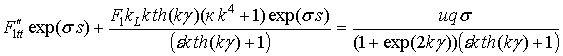 .
.
После умножения обеих частей уравнения на![]() получается следующее линейное дифференциальное неоднородное уравнение второго порядка с постоянными коэффициентами для функции F1:
получается следующее линейное дифференциальное неоднородное уравнение второго порядка с постоянными коэффициентами для функции F1:
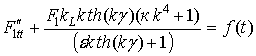 ,
,
где f(t)=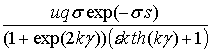 .
.
Данное уравнение решается с использованием преобразования Лапласа и начальных условий (2.39) следующим образом. Сначала необходимо получить уравнение для изображений функций F1 и f(t):
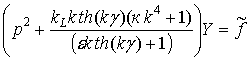 ,
,
здесь Y это изображение по Лапласу для функции F1, а![]() - изображение для функции f. Далее выражение для Y имеет вид:
- изображение для функции f. Далее выражение для Y имеет вид:
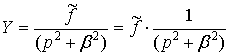 .
.
, где 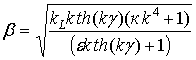
Используя таблицу преобразований Лапласа, найдем оригинал для функции 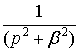 , это будет функция
, это будет функция 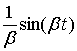 .
.
Пользуясь теоремой о свертке, получим следующее выражение для F1:
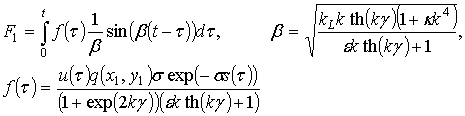 . (2.59)
. (2.59)
Подстановка (2.56) и (2.58) в (2.55) дает следующее выражение для функции F(x,y,z,t):
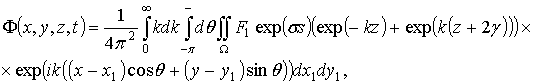 (2.60)
(2.60)
где F1 – вычисляется по (2.59).
Для нахождения волнового сопротивления R по формуле (2.36) необходимо выразить функцию w через функции F и q. Для этого рассматривается граничное условие (2.53) в безразмерном виде:
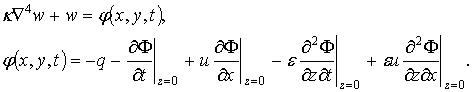 (2.61)
(2.61)
Далее проводится асимптотический анализ уравнения (2.61) в зависимости от величины параметра k. Для малых значений , которые соответствуют тонкому льду и большим размерам судна, решение уравнения (2.61) ищется в виде ![]()
Подстановка этого выражения в (2.61) дает следующие значения для функций ![]() ,
, ![]() иwi:
иwi:
![]()
![]()
![]() .
.
Далее с учетом вида функции ![]() (2.61) и разложений (2.60) и (2.55) можно получить для функции wi выражение вида
(2.61) и разложений (2.60) и (2.55) можно получить для функции wi выражение вида
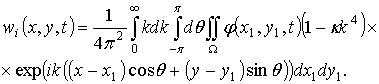 (2.62)
(2.62)
Для больших значений![]() (толстый лед, малые размеры судна) асимптотическое решение уравнения (2.61) ищется в виде
(толстый лед, малые размеры судна) асимптотическое решение уравнения (2.61) ищется в виде![]() где
где![]() – решение уравнения
– решение уравнения
![]() . (2.63)
. (2.63)
Заметим, что любое решение уравнения![]() всегда будет симметрично относительно плоскости yOz, и, следовательно, давать нулевое волновое сопротивление R (смотреть формулу (2.36)). Предполагается, что для
всегда будет симметрично относительно плоскости yOz, и, следовательно, давать нулевое волновое сопротивление R (смотреть формулу (2.36)). Предполагается, что для![]() частным решением уравнения (2.63) будет
частным решением уравнения (2.63) будет ![]() . Тогда c учетом (2.62) выражение для функции w можно записать в виде:
. Тогда c учетом (2.62) выражение для функции w можно записать в виде:
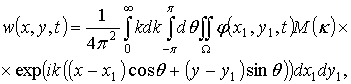 (2.64)
(2.64)
где![]() (2.65)
(2.65)
![]() (2.66)
(2.66)
Таким образом, имеются двусторонние асимптотические разложения для величины![]() при малых и больших k. Для построения интерполяционной формулы, описывающей величину
при малых и больших k. Для построения интерполяционной формулы, описывающей величину![]() в области
в области![]() применяется метод асимптотической интерполяции. В соответствии с этим методом величину
применяется метод асимптотической интерполяции. В соответствии с этим методом величину ![]() предлагается находить в виде формулы
предлагается находить в виде формулы
![]() (2.67)
(2.67)
которая сохраняет тот же порядок точности при ![]() , что и асимптотика (2.65). Функция
, что и асимптотика (2.65). Функция ![]() задается априорно и зависит от нескольких параметров, которые подбираются далее из условия, чтобы приближенная формула (2.67) с заданной точностью давала правильный асимптотический результат в другом предельном случае при
задается априорно и зависит от нескольких параметров, которые подбираются далее из условия, чтобы приближенная формула (2.67) с заданной точностью давала правильный асимптотический результат в другом предельном случае при ![]() . В частном случае, когда известен только старший член асимптотики
. В частном случае, когда известен только старший член асимптотики![]() при
при![]() (2.66), в качестве такой функции рекомендуется [54] брать
(2.66), в качестве такой функции рекомендуется [54] брать ![]() . При
. При ![]() в результате предельного перехода при
в результате предельного перехода при![]() и последующего сопоставления выражений (2.66) и (2.67) получается, что
и последующего сопоставления выражений (2.66) и (2.67) получается, что ![]() и, следовательно,
и, следовательно,![]() . Таким образом, с учетом (2.64) выражение для w запишется в виде:
. Таким образом, с учетом (2.64) выражение для w запишется в виде:
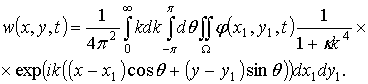 (2.68)
(2.68)
где ![]() имеет вид (2.61), а
имеет вид (2.61), а ![]() имеет вид (2.60).
имеет вид (2.60).
Подставляя (2.68) в (2.36) с учетом (2.42), (2.53), (2.59)-(2.61), делая замену переменных![]() и
и ![]() , после несложных преобразований по аналогии с [66] можно получить формулу для безразмерного коэффициента волнового сопротивления A:
, после несложных преобразований по аналогии с [66] можно получить формулу для безразмерного коэффициента волнового сопротивления A:
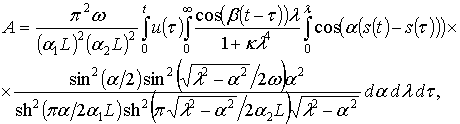 (2.69)
(2.69)
![]() ;
;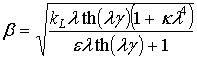 ;
;
где![]() s(t), s(t) – вычисляются по формулам (2.40) и (2.41) в безразмерном виде.
s(t), s(t) – вычисляются по формулам (2.40) и (2.41) в безразмерном виде.
Для сравнения результатов формулы (2.69) при движении по первому режиму «разгон – движение с заданной скоростью» с выходом на заданную скорость и последующий стационарный режим приведем полученную ранее формулу расчета волнового сопротивления СВП при стационарном движении по упругой пластине:
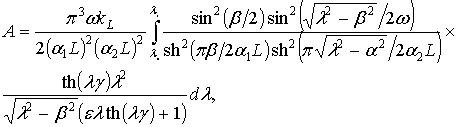 (2.70)
(2.70)
в которой все обозначения аналогичны формуле (2.69); ![]() ,
,![]() – действительные положительные корни уравнения
– действительные положительные корни уравнения
![]() .
.
Кроме того, рассмотрим полученную ранее [60] формулу для волнового сопротивления СВП при стационарном движении по вязко-упругой ледовой пластине:
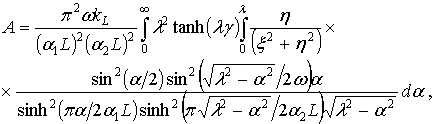 (2.71)
(2.71)
![]() ,
,
![]() ,
,![]() ,
,
где![]() - время релаксации льда для модели Кельвина-Фойгта.
- время релаксации льда для модели Кельвина-Фойгта.
Формула (2.69) должна описывать все режимы движения, в том числе и выход на стационарный режим после начального ускорения. Интересно будет проанализировать, насколько результаты, полученные для нестационарного режима движения при выходе судна на постоянную скорость движения, согласуются с известными стационарными результатами.
Численные расчеты по формулам (2.69)-(2.71) проводились для следующих значений параметров:
![]() ;
;![]() ;
;![]() ;
;
![]() ,
, ![]() ,
,![]() .
.
Заметим, что все результаты численных расчетов приведены на рисунках для размерных величин t, u, t2, t3, m1, m2, m3, u1, u2, u3.
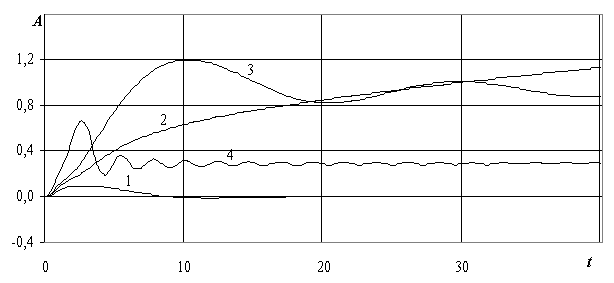
На рис. 2.29 и рис. 2.30 показаны зависимости безразмерного коэффициента волнового сопротивления А от времени t для движения судна по тонкому льду (L=10 м; h=0.1 м; e =0.009; k=4.78?*10-3; umin=6.725 м/с) по первому режиму (разгон – движение с заданной скоростью) на мелкой (γ=0.3) и глубокой (γ =1) воде соответственно.
 .
.
Рис. 2.29. Волновое сопротивление СВП в зависимости от времени t для k=4.78*10-3, g=0.3, m1=0.6 с-1:1 – u1=u2=u3=0.5umin; 2 – u1=u2=u3 =0.8umin; 3 – u1=u2=u3=umin; 4 – u1=u2=u3=2umin.
 .
.
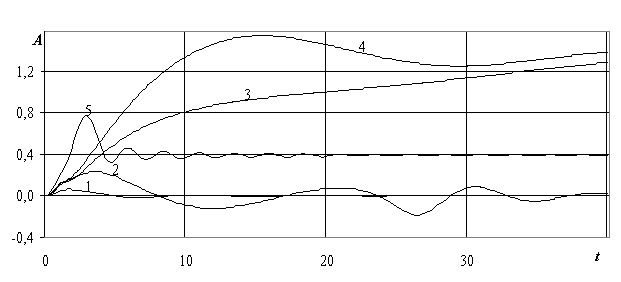
Рис. 2.30. Волновое сопротивление СВП в зависимости от времени t для k=4.78*10-3 , g=1, m1=0.6 с-1: 1 – u1=u2=u3=0.5umin; 2 – u1=u2=u3 =0.8umin; 3 – u1=u2=u3=umin; 4 – u1=u2=u3=1.1umin; 5 – u1=u2=u3=2umin.
Заметим, что для рассматриваемых на рис. 2.29 и 2.30 режимов движения СВП уже в течение первых 5-7 секунд выходит на движение с постоянной скоростью u1. Можно заметить, что значения волнового сопротивления СВП также в течение примерно 10 секунд выходят на некоторые постоянные значения и далее колеблются около этих постоянных значений. На рис. 2.29 и 2.30 хорошо просматривается зависимость волнового сопротивления от значения скорости u1, на которую выходит судно при движении. Видно, что при критических и околокритических скоростях судно испытывает наибольшее волновое сопротивление. При выходе на сверхкритическую скорость значение волнового сопротивления СВП «переходит» через «горб» волнового сопротивления и затем уменьшается до некоторого стационарного значения, гораздо меньшего, чем значение волнового сопротивления для околокритической скорости.
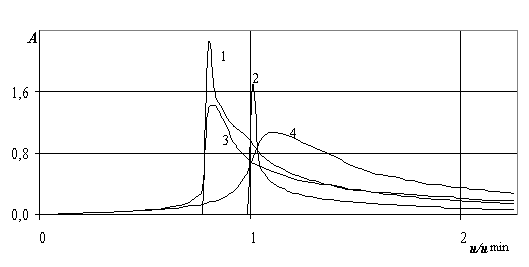
На рис. 2.31 показан для сравнения коэффициент А, рассчитанный по формулам (2.70) и (2.71) для стационарного движения СВП по тонкой ледовой упругой (кривые 1 и 2) и вязко-упругой (кривые 3 и 4) пластине для различных значений глубины водоема в зависимости от значений относительной скорости u/umin при L=10 м; h=0.1 м; e =0.009; k=4.78?*10-3; umin=6.725 м/с. Видно, что кривые волнового сопротивления на рисунках 2.24 и 2.25 с течением времени выходят на свои стационарные значения. Таким образом, формула (2.69) хорошо описывает движение с постоянной скоростью и согласуется с известными теоретическими результатами. Следовательно, использование метода асимптотической интерполяции приемлемо для вычисления прогиба пластины при нестационарном движении СВП.
 .
.
Рис.2.31. Волновое сопротивление СВП для стационарного движения в зависимости от u/umin: 1 - g =0.3, k=4.78*10-3; 2 - g= 1, k=4.78*10-3 ; 3 - g =0.3, k=4.78*10-3, tК=0.1; 4 - g= 1, k=4.78*10-3, tК=0.1.
Заметим, что для упругой пластины для скоростей, меньших umin , волновое сопротивление СВП, вычисленное по формуле (2.70) чисто мнимая величина, на рис. 2.31 оно равно нулю. Для вязко-упругой пластины при нестационарном движении по ней нагрузки волновое сопротивление близко к нулю, но отлично от нуля (см. формулу (2.71) и работу [60]). Волновое сопротивление, вычисленное по формуле (2.69), для движения нагрузки (СВП) с докритическими скоростями (кривая 1 на рис. 2.29 и кривые 2, 3 на рис. 2.30), колеблется с малой амплитудой возле нулевого значения.
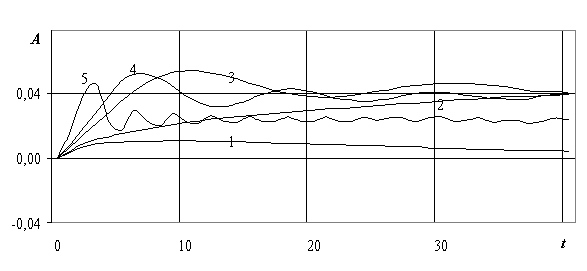
На рис. 2.32 – 2.33 показано волновое сопротивление А в зависимости от времени t для нестационарного движения судна по толстому льду (L=10 м; h=0.5 м; e =0.045; k=0.598; umin=12.297 м/с) по первому режиму (разгон – движение с заданной скоростью) на мелкой (γ =0.3) и глубокой (γ =1) воде соответственно.
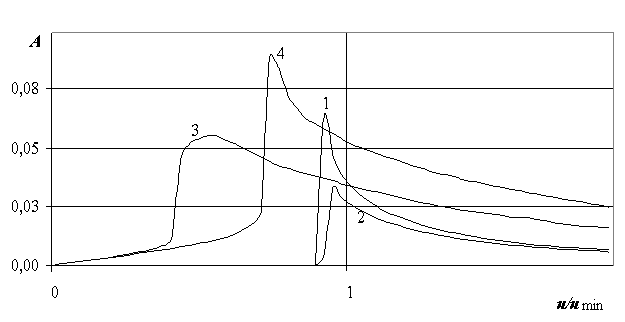
На рис. 2.34 показан для сравнения коэффициент А, рассчитанный по (2.70) – (2.71) для стационарного движения СВП по толстой ледовой упругой (кривые 1-2) и вязкоупругой (кривые 3-4) пластине для различных значений глубины водоема (L=10 м; h=0.5 м; e =0.009; k=0.598; umin=12.297 м/с). Видно, что кривые волнового сопротивления рис. 2.32 – 2.33 с течением времени выходят на свои стационарные значения.
 .
.
Рис. 2.32. Волновое сопротивление СВП в зависимости от времени при k=0.598, g=0.3, m1=0.6 с-1: 1 – u1=u2=u3=0.4umin; 2 – u1=u2=u3 =0.5umin; 3 – u1=u2=u3=0.8umin; 4 – u1=u2=u3=umin; 5 – u1=u2=u3=2umin.
 .
.
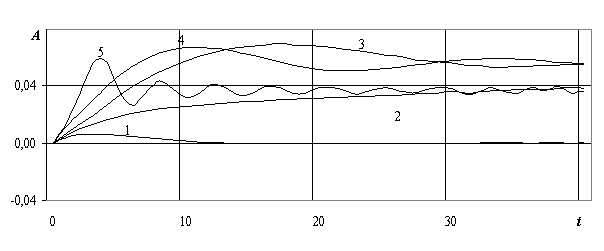
Рис. 2.33. Волновое сопротивление СВП в зависимости от времени для k=0.598, g=1, m1=0.6 с-1: 1 – u1=u2=u3=0.5umin; 2 – u1=u2=u3 =0.8umin; 3 – u1=u2=u3=umin; 4 – u1=u2=u3=1.1umin; 5 – u1=u2=u3=2umin.
 .
.
Рис. 2.34. Волновое сопротивление СВП при стационарном движении в зависимости от u/umin: 1 - g =0.3, k=0.598; 2 - g= 1, k=0.598;3 - g =0.3, k=0.598, tК=0.1; 4 - g= 1, k=0.598, tК=0.1.
Из сравнения рис. 2.29 – 2.34 видно, что увеличение толщины льда приводит к уменьшению волнового сопротивления. Увеличение глубины водоема дает увеличение волнового сопротивления при движении на сверхкритических скоростях. На глубокой воде значение критических скоростей (соответствующих наибольшему волновому сопротивлению) близко к umin, а для мелкой воды критические скорости меньше, чем umin. Увеличение толщины льда также приводит к уменьшению значений критических скоростей u/umin.
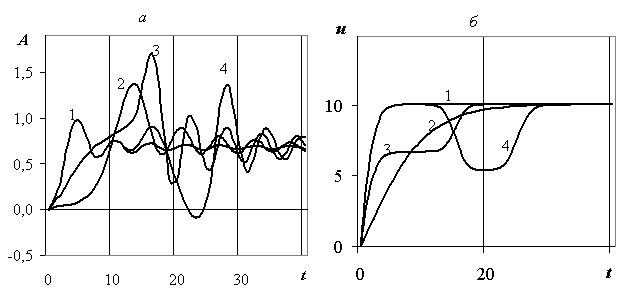
На рис. 2.35 – 2.36 показано влияние различных режимов ускорения и торможения на волновое сопротивление СВП для L=10 м; h=0.1 м; e =0.009; k=4.78?*10-3; umin=6.725 м/с, γ=1. Из анализа кривых 1 и 2 (рис. 2.35-2.36) видно, что чем больше начальное ускорение при выходе судна на сверхкритическую скорость, тем меньше максимум волнового сопротивления СВП. Кривая 3 (рис. 2.35) показывает, что выход на сверхкритическую скорость по третьему режиму после движения на критической скорости также увеличивает волновое сопротивление СВП. Кривая 4 (рис. 2.35) демонстрирует, что выход на сверхкритическую скорость, затем торможение до докритической скорости и последующий разгон до сверхкритической скорости также обеспечивает повышение волнового сопротивления.
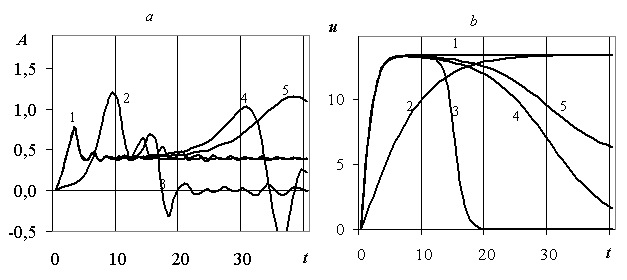
Кривые 3 и 4 рис. 2.36 показывают, что при выходе на сверхкритическую скорость и последующем торможении до нуля волновое сопротивление по абсолютной величине будет тем больше, чем меньше абсолютное значение ускорения. Кривая 5 рис. 2.36 показывает, что торможение от сверхкритической скорости до докритической с малым коэффициентом торможения приводит к росту волнового сопротивления.
 .
.
Рис. 2.35. Волновое сопротивление СВП (а) и соответствующая скорость СВП (б) в зависимости от времени для k=4.78*10-3, g=1:1 – u1=u2=u3=1.5umin, m1=0.5 с-1;2 – u1=u2=u3=1.5umin, m1=0.1 с-1;3 – u1= umin, u2=u3=1.5umin, m1=0.5 с-1, m2=0.6 с-1 , t2=15 с;4 – u1=1.5umin, u2=0.8umin, u3=1.5umin, m1=0.5 с-1 , m2=0.6 с-1 , m3=0.5 с-1,t2=15 с, t3=25 с.
 .
.
Рис. 2.36. Волновое сопротивление (а) и соответствующая скорость СВП (б) в зависимости от времени для k=4.78*10-3, g=1: 1 – u1=u2=u3=2umin, m1=0.5 с-1;2 – u1=u2=u3=2umin, m1=0.1 с-1 ;3 – u1=2umin, u2=u3=0, m1=0.5 с-1 , m2=0.6 с-1, t2=15 с;4 – u1=2umin, u2=u3=0, m1=0.5 с-1, m2=0.1 с-1, t2=30 с;5 – u1=2umin, u2=u3=0.8umin, m1=0.5 с-1 , m2=0.1 с-1 , t2=30 с.
Полученная аналитическая формула (2.69) и численные расчеты по ней позволили проанализировать влияние глубины водоема, толщины льда, размеров судна и режимов движения на волновое сопротивление СВП при нестационарном движении по ледяному покрову. Так как эти результаты можно распространить на движение любой распределенной нагрузки по ледяному покрову (машина, самолет, аэросани и т.д.), далее при формулировке выводов используется слово «нагрузка», а не СВП.
Результаты расчетов показали, что наименьшее волновое сопротивление испытывает нагрузка, движущаяся на очень малых докритических скоростях или на очень больших сверхкритических скоростях. Если нагрузка ускоряется до сверхкритической скорости или тормозит до докритической скорости и при этом необходимо сохранить целостность ледяного покрова, то для уменьшения волнового сопротивления (понижения вероятности разрушения льда) необходимо ускоряться или тормозить, по возможности, с наибольшим коэффициентом ускорения.
Наибольшее волновое сопротивление испытывает нагрузка, движущаяся на околокритических скоростях движения. В случае тонкого льда и большой глубины водоема, когда ![]() , значение околокритической скорости нагрузки близко к
, значение околокритической скорости нагрузки близко к ![]() . В случае толстого льда и малой глубины водоема, когда
. В случае толстого льда и малой глубины водоема, когда ![]() , значение околокритической скорости близко к
, значение околокритической скорости близко к ![]() и лежит в интервале
и лежит в интервале ![]() . При торможении и ускорении нагрузки наибольшее волновое сопротивление возникает в случае «слабого» (с наименьшим коэффициентом ускорения) или «постепенного» ускорения и торможения.
. При торможении и ускорении нагрузки наибольшее волновое сопротивление возникает в случае «слабого» (с наименьшим коэффициентом ускорения) или «постепенного» ускорения и торможения.
Получения близкого к нулю волнового сопротивления для докритических скоростей движения, по-видимому, можно избежать, введя в условие задачи время релаксации льда и рассмотрев вязко-упругую ледяную пластину.