Научная электронная библиотека

Монографии, изданные в издательстве Российской Академии Естествознания

Прикладные задачи динамики ледяного покрова

Козин В. М., Жесткая В. Д., Погорелова А. В., Чижиумов С. Д., Джабраилов М. Р., Морозов В. С., Кустов А. Н.,

2.2.3. Влияние вязкостных свойств пластины на волновое сопротивление нестационарно движущейся нагрузки

Рассмотрим бесконечную область, покрытую сплошным льдом, по которой со скоростью u(t) перемещается заданная система поверхностных давлений q. Совмещенная с судном система координат располагается следующим образом: плоскость xOy совпадает с невозмущенной поверхностью раздела лед – вода, ось x направлена в сторону движения судна, ось z – вертикально вверх. Предполагается, что вода – идеальная несжимаемая жидкость плотности r₂, движение жидкости потенциальное. Ледяной покров моделируется вязко-упругой, изначально ненапряженной однородной изотропной пластиной. Предполагается, что период волновых процессов в ледяном покрове много меньше времени релаксации льда. Согласно работе [124], для льда принимается закон деформирования линейной упруго запаздывающей среды Кельвина-Фойгта [122].

Величина волнового сопротивления, действующего на СВП, вычисляется согласно [17, 109] по формуле (2.36)

Линеаризованное кинематическое условие на поверхности раздела лед – вода имеет вид (2.52).

Исходя из сделанных предположений, линеаризованные граничные условия для w и F запишутся как:

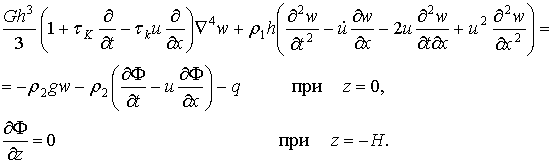(2.72)

Здесь G – модуль упругости льда при сдвиге, G=0,5E/(1+n), - модуль Юнга, - коэффициент Пуассона; t_К - время релаксации деформаций льда или «время запаздывания» [122, 124], h(x,y) - толщина льда, r₁(x,y) – плотность льда; H=H₁-b; H₁ – глубина водоема; b=r₁h/r₂ – глубина погружения льда при статическом равновесии. Для больших глубин, когда H₁ намного больше h, можно считать H » H₁. В дальнейшем предполагается, что величины r₁ и h – постоянные. В качестве расчетных величин G и r₁ следует принимать их приведенные значения, определяемые как интегральные величины по толщине пластины.

При условии, что в момент времени t=0 судно не имеет хода и отсутствуют любые возмущения, кроме статической деформации ледовой пластины, начальные условия для функции F(x,y,z,t) запишутся в виде (2.39).

Предполагается, что закон изменения скорости СВП в зависимости от времени приближенно выражается формулой (2.40), а расстояние, пройденное судном, по формуле (2.41).

Предполагается, что в заданной подвижной системе координат давление q не зависит от времени и имеет вид (2.42).

Для аналитического решения задачи совершается переход к безразмерной постановке. Для этого вводятся характерный размер L – длина судна и характерная скорость u₀, в качестве которой в дальнейшем выбирается минимальная фазовая скорость [124], где . Вводятся безразмерные переменные, функции и параметры:

, , , , ,, .

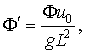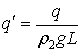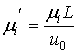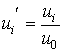
(штрихи в дальнейшем будем опускать). Комбинированное (2.52) и (2.72) безразмерное граничное условие для z=0 имеет вид:

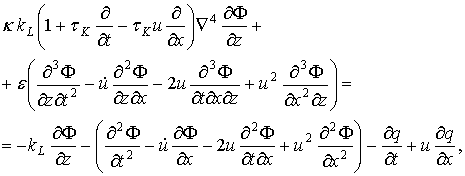(2.73)

где , , .

Кроме того, следуя [63, 139], предполагается, что функциии удовлетворяют условиям, необходимым для представления их в виде разложения в интегралы Фурье по двум переменным x и y:

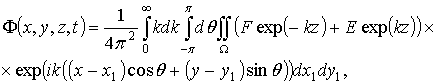
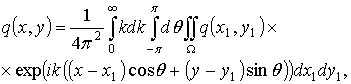(2.74)

где F и E – неизвестные функции переменных x₁, y₁, t, k, q. Подстановка выражений (2.74) в граничное условие (2.73) и обезразмеренное граничное условие (2.72) для , где , позволяет получить зависимость между величинами F и E и дифференциальное уравнение для F:

(2.75)

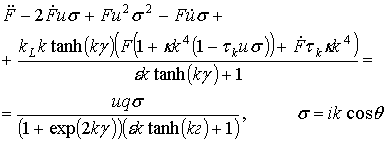(2.76)

Для решения (2.76) по аналогии с [63, 139] вводится в рассмотрение функция

(2.77)

где- безразмерное расстояние, пройденное СВП за время t.

Подстановка (2.77) в (2.76) приводит уравнение (2.76) к виду:

.

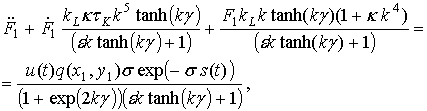решение которого с использованием преобразования Лапласа, начальных условий (2.39) и теоремы о свертке позволяет получить следующее выражение для величины F₁:

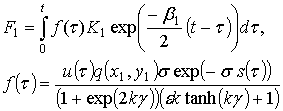(2.78)

, .

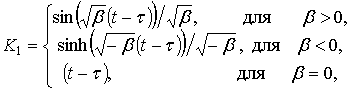
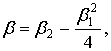
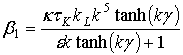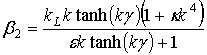Подстановка (2.75) и (2.77) в (2.74) дает следующее выражение для функции F:

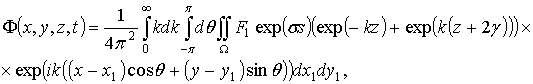(2.79)

где F₁ – вычисляется по (2.78).

Для нахождения волнового сопротивления R по формуле (2.36) необходимо выразить w через функции F и q. Для этого рассматривается граничное условие (2.72) в безразмерном виде:

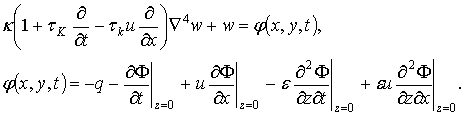(2.80)

Далее проводится асимптотический анализ уравнения (2.80) в зависимости от величины параметра k. Для малых значений , которые соответствуют тонкому льду и большим размерам судна, асимптотическое решение уравнения (2.80) ищется в виде:

(2.81)

Подстановка (2.81) в (2.80) дает следующие значения для функций , и w_i:

,

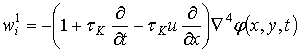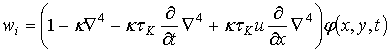. (2.82)

Принимая для упрощения решения в (2.82)(время релаксации равно нулю, пластина чисто упругая) с учетом вида функции j (2.80) и разложений (2.74) и (2.79) можно получить для выражение вида

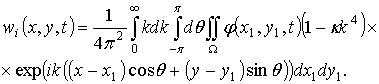(2.83)

Для больших значений (толстый лед, малые размеры судна) асимптотическое решение уравнения (2.80) ищется в виде где – решение уравнения

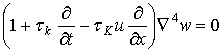. (2.84)

Заметим, что любое решение уравнениявсегда будет симметрично относительно плоскости yOz, и, следовательно, давать нулевое волновое сопротивление R (смотреть формулу (2.36)). Предполагается, что для частным решением уравнения (2.84) будет . Тогда c учетом уравнения (2.83) выражение для функции w можно записать в виде:

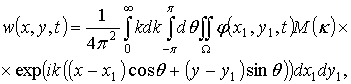(2.85)

где(2.86)

(2.87)

Таким образом, имеются двусторонние асимптотические разложения для величиныпри малых и больших k. Для построения интерполяционной формулы, описывающей величинув областиприменяется метод асимптотической интерполяции. В соответствии с этим методом величину предлагается находить в виде формулы

(2.88)

которая сохраняет тот же порядок точности при , что и асимптотика (2.86). Функция задается априорно и зависит от нескольких параметров, которые подбираются далее из условия, чтобы приближенная формула (2.88) с заданной точностью давала правильный асимптотический результат в другом предельном случае при . В частном случае, когда известен только старший член асимптотики при (2.87), в качестве такой функции рекомендуется брать . Прив результате предельного перехода при и последующего сопоставления выражений (2.87) и (2.88) получается, чтои, следовательно, . Таким образом, с учетом (2.85) выражение для w запишется в виде:

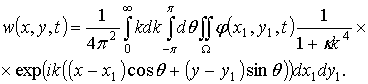(2.88)

гдеимеет вид (2.80), а имеет вид (2.79).

Подставляя (2.88) в (2.36) с учетом (2.42), (2.74), (2.78)-(2.80), делая замену переменных ипосле несложных преобразований по аналогии с [139], [63] можно получить формулу для безразмерного коэффициента волнового сопротивления A:

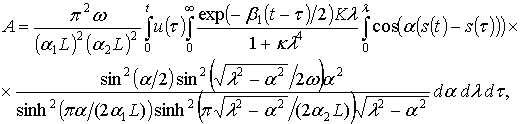(2.89)

,

;

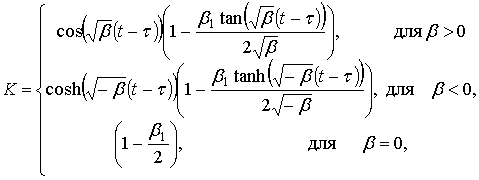
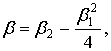
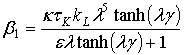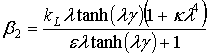
где s(t), s(t) – вычисляются по формулам (2.40) и (2.41) в безразмерном виде.

Численные расчеты по формуле (2.89) проводились для следующих значений параметров:

; ; ;

, , , .

Время релаксации выбиралось в соответствии с результатами работ [2, 26]. Заметим, что далее на рисунках все результаты численных расчетов приведены для размерных величин t, u, t₂, t₃, m₁, m₂, m₃, u₁, u₂, u₃, .

.

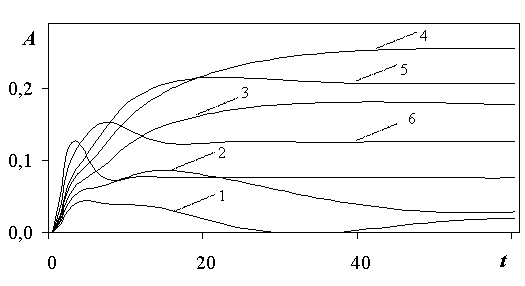
Рис. 2.37. Волновое сопротивление при L=10 м; h=0,2 м; e =0,018; k=0,038; u_min=8,721 м/с, t_k=0,69 с, g=4, m₁=0,5 с^-1 в зависимости от времени: 1 - u₁= u₂= u₃= 0,6u_min м/с; 2 - u₁= u₂= u₃= 0,8u_min м/с; 3 - u₁= u₂= u₃= u_min м/с; 4 - u₁= u₂= u₃= 1,2u_min м/с;5 - u₁= u₂= u₃= 1,4u_min м/с; 6 - u₁= u₂= u₃= 2u_min м/с;7 - u₁= u₂= u₃= 3u_min м/с.

На рис.2.37 показана зависимость безразмерного коэффициента волнового сопротивления А от времени t для движения судна в первом режиме для L=10 м, g=4, h=0,2 м; e =0,018; k=0,038; u_min=8,721 м/с. Из рисунка видно, что после разгона и выхода СВП на равномерное движение, его волновое сопротивление с течением времени выходит на некоторые постоянные значения, зависящие от скорости. Причем, в отличие от результатов работы , в которой лед моделировался чисто упругой пластиной, эти значения не имеют колебательного характера. Из рисунка видно, что наибольшее волновое сопротивление судно имеет при скоростях равных u_min¸1,4u_min м/c (кривые 3-5). При выходе судна после разгона на докритические скорости (u₁<u_min) волновое сопротивление мало (кривые 1, 2), но, в отличие от работы [56], не равно нулю. Если же судно после разгона выходит на сверхкритические скорости (u₁>1,4u_min) (кривые 6, 7), то волновое сопротивление сначала растет, затем, не достигнув критических значений, начинает падать и выходит на некоторые постоянные значение, которые гораздо меньше критических. Интересно сравнить значения волнового сопротивления, которые получает судно при равномерном движении после разгона с результатами стационарной задачи о движении судна по вязко-упругой пластине [60].

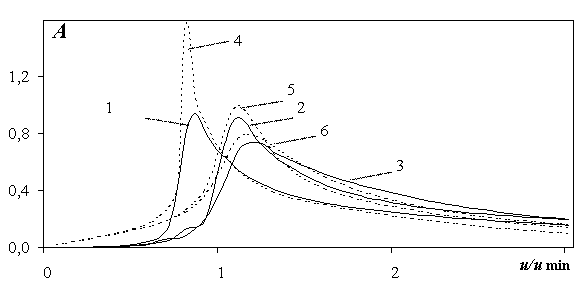
На рис. 2.38 и 2.39 представлено волновое сопротивление судна в зависимости от скорости движения для тонкого и толстого льда соответственно. Здесь кривыми (1-3) обозначены результаты, полученные по формуле (2.89) для t=100 при равномерном движении с заданной скоростью u₁ после разгона (нестационарное решение, первый режим движения), кривыми (4-6) обозначены расчеты по формулам работы [60] (стационарное решение задачи). Из анализа кривых рис.2.38 – 2.39 следует, что нестационарное решение близко к стационарному и немного превышает его для сверхкритических скоростей (u>1,4u_min), а для критических и докритические скоростей расхождение в результатах более заметное. Тем не менее, значения скоростей, соответствующих максимальному волновому сопротивлению, совпадают для стационарного и нестационарного решения: для малой и конечной глубины критическая скорость близка к значению , а для большой и бесконечной глубины близка к 1,1u_min¸1,2u_min

.

Рис. 2.38. Волновое сопротивление СВП в зависимости от скорости u при равномерном движении для нестационарного (кривые 1-3) и стационарного (кривые 4-6) решения при L=10 м; h=0,1 м; e =0,009; k=4,783*10^-3; u_min=6,725 м/с, t_k=0,69 с:1 – u₁= u₂= u₃= u, m₁=0,5 с^-1, t=100 c, g=0,3;2 - u₁= u₂= u₃= u, m₁=0,5 с^-1, t=100 c, g=0,7;3 - u₁= u₂= u₃= u, m₁=0,5 с^-1, t=100 c, g=4;4 - g=0,3; 5 - g=0,7; 6 - g=4.

Увеличение толщины льда приводит к уменьшению коэффициента волнового сопротивления. При движении на сверхкритических скоростях уменьшение глубины водоема дает некоторое уменьшение волнового сопротивления для различной толщины льда.

.

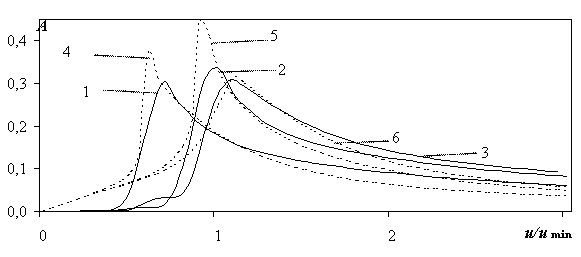
Рис. 2.39. Волновое сопротивление СВП в зависимости от скорости u при равномерном движении для нестационарного (кривые 1-3) и стационарного (кривые 4-6) решения при L=20 м; h=0,5 м; e =0,023; k=0,037; u_min=12,297 м/с, t_k=0,69 с:1 – u₁= u₂= u₃= u, m₁=0,5 с^-1, t=100 c, g=0,25;2 - u₁= u₂= u₃= u, m₁=0,5 с^-1, t=100 c, g=0,7;3 - u₁= u₂= u₃= u, m₁=0,5 с^-1, t=100 c, g=3;4 - g=0,25; 5 - g=0,7; 6 - g=3.

.

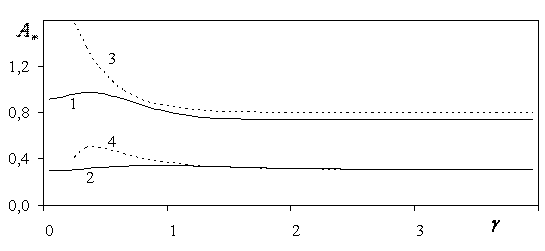
Рис. 2.40. Максимальное волновое сопротивление судна при равномерном движении в зависимости от g для нестационарного (кривые 1-2) и стационарного (кривые 3-4) решения приt_k=0,69 с: 1 – u₁= u₂= u₃= u, m₁=0,5 с^-1, t=100 c, L=10 м, h=0,1 м, e =0,009; k=4,783*10^-3, u_min=6,725 м/с;2 – u₁= u₂= u₃= u, m₁=0,5 с^-1, t=100 c, L=20 м; h=0,5 м; e =0,023; k=0,037, u_min=12,297 м/с;3 - L=10 м, h=0,1 м, e =0,009; k=4,783*10^-3;4 - L=20 м; h=0,5 м; e =0,023; k=0,037.

На рис.2.40 показаны максимальные значения волнового сопротивления для разной глубины водоема g при равномерном движении. Здесь кривые 1-2 соответствуют равномерному движению судна после разгона (нестационарное решение, формула (2.89)), кривые 3-4 соответствуют стационарному решению задачи (вычислены по формулам работы [60]). Видно, что при нестационарном решении задачи влияние глубины на максимальное значение волнового сопротивления носит немонотонный характер: максимум волнового сопротивления в зависимости от толщины льда находится в области g=0,5¸1. С увеличением глубины волновое сопротивление падает и выходит на постоянное значение в области g>1,5. Для очень малой глубины нестационарное решение также дает уменьшение волнового сопротивления. Аналогичный эффект уменьшения волнового сопротивления на малой глубине наблюдался в экспериментальной части работы . Уменьшение глубины для стационарного решения дает неоднозначные зависимости: для тонкого льда происходит увеличение волнового сопротивления, а для толстого - уменьшение, причем для малых значений g решение расходится. Для толстого льда при нестационарном режиме движения значение глубины g почти не влияет на максимальное значение волнового сопротивления. Расхождение между стационарными и нестационарными значениями волнового сопротивления в области малых g, по-видимому, объясняется некоторым несовершенством линейной теории волн. Как известно [44], применение линейной теории волн более оправдано при нестационарном решении задачи.

.

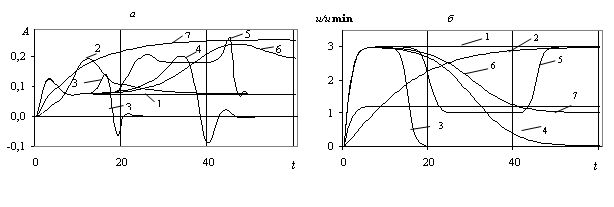
Рис. 2.41. Волновое сопротивление (а) и скорость СВП (б) в зависимости от времени для L=10 м; h=0,2 м; e =0,018; k=0,038; u_min=8,721 м/с, t_k=0,69 с, g=4: 1 - u₁= u₂= u₃= 3u_min м/с; m₁=0,5 с^-1;2 - u₁= u₂= u₃= 3u_min /с; m₁=0,05 с^-1;3 - u₁= 3u_min м/с; u₂= u₃=0 м/с; m₁=0,5 с^-1; m₂=0,6 с^-1; t₂=15с;4 - u₁= 3u_min м/с; u₂= u₃=0 м/с; m₁=0,5 с^-1; m₂=0,1 с^-1; t₂=30с;5 - u₁= 3u_min м/с; u₂= u_min м/с; u₃=3 м/с; m₁=0,5 с^-1; m₂=0,5 с^-1; ₃=0,6 с^-1; t₂=20с; t₃=45с;6 - u₁= 3u_min м/с; u₂= u₃= u_min м/с; m₁=0,5 с^-1; m₂=0,1 с^-1; t₂=30с;7 - u₁= u₂= u₃= 1,2u_min м/с, m₁=0,5 с^-1.

На рис. 2.41 показано влияние различных режимов ускорения и торможения на волновое сопротивление СВП для L=10 м; h=0,2 м; e =0,018; k=0,038; u_min=8,721 м/с, g=4. Из анализа кривых 1 и 2 видно, что чем больше начальное ускорение при выходе судна на сверхкритическую скорость, тем меньше максимум волнового сопротивления СВП. Данный вывод согласуется с результатами работ [63, 139] для равноускоренного движения СВП по чистой воде и в поле битого льда. Кривые 3 и 4 показывают, что при выходе на сверхкритическую скорость и последующем торможении до нуля волновое сопротивление по абсолютной величине будет тем больше, чем меньше абсолютное значение коэффициента торможения. Кривая 5 демонстрирует, что выход на сверхкритическую скорость, затем торможение до докритической скорости и последующий разгон до сверхкритической скорости также обеспечивает повышение волнового сопротивления. Кривая 6 показывает, что торможение от сверхкритической скорости до докритической с малым коэффициентом торможения приводит к росту волнового сопротивления. Кривая 7 приведена для сравнения с остальными кривыми и демонстрирует волновое сопротивление при разгоне до критической скорости и дальнейшем движении с критической скоростью.

На рис. 2.41 показано влияние различных режимов ускорения и торможения на волновое сопротивление СВП для L=10 м; h=0,2 м; e =0,018; k=0,038; u_min=8,721 м/с, g=4. Из анализа кривых 1 и 2 видно, что чем больше начальное ускорение при выходе судна на сверхкритическую скорость, тем меньше максимум волнового сопротивления СВП. Данный вывод согласуется с результатами работ [63, 139] для равноускоренного движения СВП по чистой воде и в поле битого льда. Кривые 3 и 4 показывают, что при выходе на сверхкритическую скорость и последующем торможении до нуля волновое сопротивление по абсолютной величине будет тем больше, чем меньше абсолютное значение коэффициента торможения. Кривая 5 демонстрирует, что выход на сверхкритическую скорость, затем торможение до докритической скорости и последующий разгон до сверхкритической скорости также обеспечивает повышение волнового сопротивления. Кривая 6 показывает, что торможение от сверхкритической скорости до докритической с малым коэффициентом торможения приводит к росту волнового сопротивления. Кривая 7 приведена для сравнения с остальными кривыми и демонстрирует волновое сопротивление при разгоне до критической скорости и дальнейшем движении с критической скоростью.