
Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания

Прикладные задачи динамики ледяного покрова
Козин В. М., Жесткая В. Д., Погорелова А. В., Чижиумов С. Д., Джабраилов М. Р., Морозов В. С., Кустов А. Н.,
3.1.2. Физическая модель
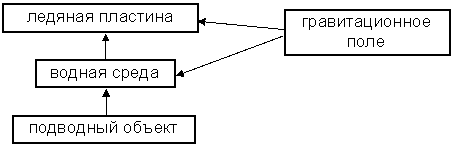
Система «подводное судно – ледяной покров» может быть схематически представлена так, как на рис. 3.1. Движение подводного судна будем считать заданным. Вокруг судна в водной среде образуется поле гидродинамических давлений, воздействующее на ледяной покров. В общем случае динамический изгиб ледяной пластины вызывает дополнительное движение жидкости. Однако, учитывая, что прогибы ледяного покрова малы по сравнению с размерами подводного объекта, при определении гидродинамических давлений от движения этого объекта на поверхность льда ледяной покров можно считать неподвижным.
Водная среда может считаться идеальной несжимаемой жидкостью, так как вблизи поверхности льда (на удалении от пограничного слоя, окружающего подводное судно) скорости потока жидкости относительно небольшие и мало отличаются от потока в идеальной среде.
Данная модель позволяет использовать известную математическую постановку гидродинамики идеальной жидкости для определения давлений водной среды на ледяную поверхность. Рассчитанные гидродинамические давления определяют внешнюю нагрузку при расчёте изгиба ледяной пластины.
 .
.
Рис. 3.1. Система «подводное судно – ледяной покров»
Динамика ледяного покрова под воздействием движущегося вдоль него поля давлений определяется при следующих допущениях. Ледяной покров моделируется упругой жёсткой пластиной, в общем случае переменной толщины. Сила поддержания воды учитывается в виде упругого основания Винклера.
К внутренним силам инерции пластины следует добавить силы инерции жидкости, вызванные упругими изгибными волнами в пластине. Инерционные свойства «присоединённой» к пластине жидкости могут быть получены из уравнений гидродинамики идеальной жидкости.
Наибольшую сложность при моделировании динамики ледяного покрова представляет учёт сил демпфирования. Эти силы имеют разную природу:
- внутреннее вязкоупругое сопротивление в ледяной пластине;
- вязкое трение жидкости о поверхность льда при наличии существенного поступательного течения;
- гидродинамическое демпфирование, обусловленное распространением гравитационных волн, образованных изгибом ледяной пластины.
Внутреннее трение при динамическом изгибе ледяного покрова наиболее часто учитывается на основе теории вязкого трения Кельвина – Фойгта, отличающейся относительной простотой и практической применимостью [38, 44, 124]. Её недостаток состоит в том, что коэффициент внутреннего поглощения и сила трения, согласно этой теории, пропорциональны частоте упругих волн, между тем как согласно опытным данным такая зависимость отсутствует [106]. В связи с этим обстоятельством на практике используется также модель Е.С. Сорокина, согласно которой внутреннее сопротивление можно определить через время релаксации деформаций, которое зависит от коэффициента внутреннего трения γ и периода изгибной волны Т
![]() ,
,
или в зависимости от длины L и скорости движения v волны (в случае движения подводного судна вблизи ледяной поверхности длина волны изгиба примерно равна длине корпуса судна)
![]() . (3.1)
. (3.1)
Вязкое трение жидкости о поверхность льда может иметь существенное значение на динамический изгиб ледяного покрова только при наличии существенных течений подо льдом, формирующим пограничный слой, например, на быстрой реке. Скорости обтекания ледяной поверхности, вызванные движением подводного объекта, малы, поэтому вязким трением жидкости можно пренебречь.
Волновое демпфирование при движении судна под сплошным ледяным покровом незначительно, однако оно может иметь существенное влияние при наличии вблизи подводного судна свободных кромок ледяного поля.