Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
Прикладные задачи динамики ледяного покрова
Козин В. М., Жесткая В. Д., Погорелова А. В., Чижиумов С. Д., Джабраилов М. Р., Морозов В. С., Кустов А. Н.,
3.2. Моделирование гидродинамических нагрузок методом граничных элементов
Постановки задач гидродинамики (3.4) – (3.7) или (3.4), (3.5), (3.7), (3.9) являются частными случаями более общей задачи:
(3.12)
(3.13)
(3.14)
где x - некоторая точка области Ω с декартовыми координатами (x, y, z); Г = Гφ + Гυ - граница области Ω; Гφ – поверхность, на которой задано значение потенциала скорости 
; Гυ – поверхность, на которой задано значение проекции скорости на нормаль 
.
Для системы (3.12) – (3.14) можно записать эквивалентное ей граничное интегральное уравнение [20, 21]:
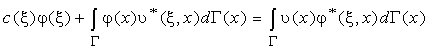(3.15)
или
,
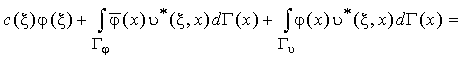
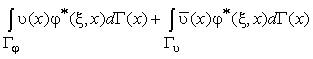где ξ – некоторая точка области Ω с декартовыми координатами (ξ, η, ζ); c(ξ) – относительный внутренний угол границы в точке ξ (для точки на гладкой границе с = 0.5, для внутренней точки с = 1);
– фундаментальное решение для уравнения Лапласа;
.
Постановка (3.15) имеет преимущество перед постановкой (3.12) – (3.14), связанное с тем, что при решении интегрального уравнения не обязательно анализировать внутренние точки области Ω. При применении численной процедуры расчётная сетка строится только по границе Г, поэтому разрешающая система алгебраических уравнений имеет существенно меньший порядок.