
Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания

Прикладные задачи динамики ледяного покрова
Козин В. М., Жесткая В. Д., Погорелова А. В., Чижиумов С. Д., Джабраилов М. Р., Морозов В. С., Кустов А. Н.,
3.2.1. Фундаментальные решения
Фундаментальное решение для оператора Лапласа можно представить как потенциал источника единичной интенсивности в бесконечной области:
![]() (3.16)
(3.16)
где ξ - точка, в которой расположен источник, x - текущая точка («точка наблюдения»), R - расстояние между этими точками.
В некоторых задачах область может быть ограничена регулярным образом. Для таких случаев можно получить фундаментальное решение, удовлетворяющее также и простым условиям на регулярных границах. Тогда интегралы в уравнениях (3.15) берутся только для той части границы Г, которая не учитывается фундаментальным решением.
Если область ограничена плоскостью, на которой задано граничное условие
![]() (3.17)
(3.17)
то фундаментальное решение будет иметь вид
![]() (3.18)
(3.18)
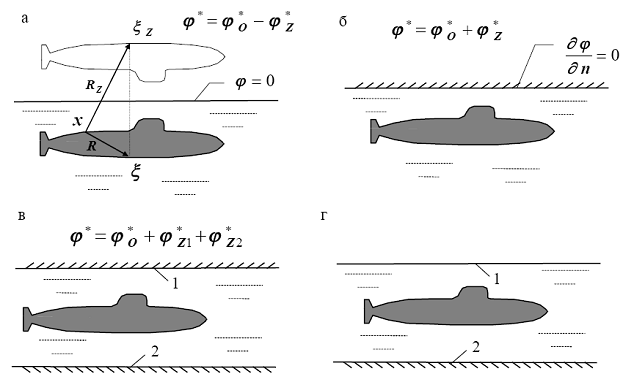
где ξz - точка, являющаяся зеркальным отражением точки ξ относительно граничной плоскости (рис. 3.2, а).
 .
.
Рис. 3.2. Функции Грина для некоторых регулярных границ
Это условие соответствует свободной поверхности воды в случаях, когда судно движется под свободной поверхностью с предельно большой скоростью или когда ограниченная пластина у свободной поверхности испытывает высокочастотные колебания (при этом скорости движения свободной поверхности направлены вертикально).
Если область ограничена плоскостью, на которой задано граничное условие твёрдой стенки
![]() (3.19)
(3.19)
то фундаментальное решение примет вид (рис. 3.2, б)
![]() (3.20)
(3.20)
Это условие соответствует поверхности воды подо льдом или на дне в случае, когда скорости течения направлены вдоль поверхности.
Фундаментальные решения, приведенные здесь, представляют собой функции Грина для различных краевых задач. Примеры применения таких функций для задачи о движении тела в идеальной жидкости приведены на рис. 3.2. В этих случаях граничное интегральное уравнение содержит интегралы только по той границе, которая не учитывается функцией Грина. В результате при его численном решении получается система линейных алгебраических уравнений (СЛАУ) существенно меньшего размера.
Погрешность применения условия (3.19) для моделирования влияния ледяного покрова в задаче об определении гидродинамических давлений на лёд от движения подводного судна связана с податливостью ледяной пластины. В большинстве случаев прогиб льда незначителен по сравнению с размерами судна и условие (3.19) вполне приемлемо.
Другой способ учёта граничных условий на дне, свободной или покрытой льдом поверхности воды, который будет рассмотрен в дальнейшем, основан на их непосредственном включении в численную модель МГЭ путём дискретизации этих границ.