Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
Прикладные задачи динамики ледяного покрова
Козин В. М., Жесткая В. Д., Погорелова А. В., Чижиумов С. Д., Джабраилов М. Р., Морозов В. С., Кустов А. Н.,
3.2.2. Граничные элементы
Метод граничных элементов является численным методом решения уравнения (3.15). Он заключается в следующем [20, 21]. Функции 
и 
представляются в виде рядов:
(3.21)
где 
и 
- значения функций в заданных точках (узлах) на границе Г,
- заданные интерполирующие функции локального вида (они не равны нулю в малых окрестностях точки i границы Г, которые называют граничными элементами), n - число узлов на границе Г. Формулы (3.21) можно представить отдельно для каждого граничного элемента k в виде
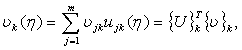(3.22)
где η - точка границы в местной нормированной системе координат граничного элемента, m - число узлов элемента.
Подставим (3.22) в (3.15). При этом заменим интегралы по границе суммами интегралов по граничным элементам, учитывая свойство локальности базисных функций. Уравнение (3.15) для каждого узла i примет вид:
, 
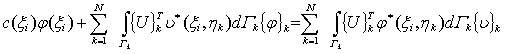(3.23)
где N - число элементов. Систему уравнений (3.23) можно записать в матричном виде
,
(3.24)
где 
и 
- заполненные, несимметричные матрицы порядка
,
и
- векторы узловых значений функций 
и 
.
В уравнения МГЭ (3.23) входят интегралы по элементам. Рассмотрим вопросы вычисления этих интегралов на примере четырехугольных граничных элементов с узлами в углах и линейными аппроксимирующими функциями. В этом случае в формулах (3.22) m = 4 , а функции формы имеют вид
,
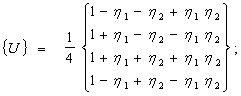(3.25)
где 
и 
- местные нормированные координаты элемента (рис. 3.3).
Здесь применяется линейное изопараметрическое отображение элемента, то есть функции (3.25) применяются не только для аппроксимации φ и υ, но и для описания геометрии элемента:
.
(3.26)
Аналогичная формула применяется для координат y и z ).
.
.
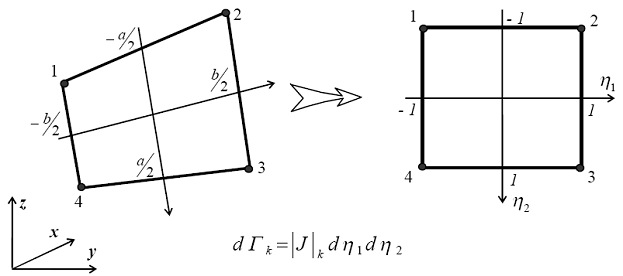Рис. 3.3. Четырехугольный элемент в общей и местнойсистемах координат
Дифференциал площади элемента
.
(3.27)
В данном случае для плоских элементов якобиан преобразования (индекс k опустим для краткости) определяется в виде:
,
(3.28)
где
 |  |
 | |
 |
(3.29)
Подставив выражение (3.26) и аналогичные формулы для координат y и z в (3.29) и выполнив операции дифференцирования, получим
|  |
 | |
 |
(3.30)
где
.
.
Индексы координат в этих формулах обозначают номера узлов элемента.
В результате система интегральных уравнений (3.23), соответствующих смешанной задаче для уравнения Лапласа, записанная в местной нормированной системе координат каждого элемента, принимает вид
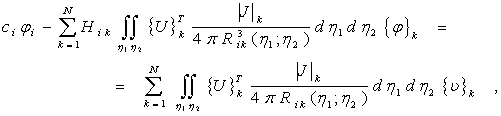(3.31)
где i = 1 , 2 , . . . n , n - число узлов сетки граничных элементов,
Hik - расстояние от точки i до плоскости элемента k ,
-расстояние от узла i до переменной точки элемента k .
Если точка i не принадлежит граничному элементу, то интегралы в уравнениях (3.31) в общем случае можно вычислить по квадратурным формулам Гаусса:
,
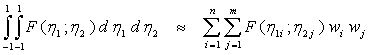(3.32)
где
- координаты точек интегрирования,
- соответствующие им весовые коэффициенты, n, m - число точек интегрирования по координатам
.
Необходимо отметить, что изменение подинтегральной функции по площади элементов существенно зависит от соотношений между размерами элементов и расстоянием точки сингулярности i до области интегрирования. Чем ближе особая точка к интегрируемой области, тем резче изменяются подинтегральные функции, а следовательно необходимо численное интегрирование с большим числом точек интегрирования n и m. Для отдаленных от точки i элементов можно ограничиться малым числом n и m.
Если особая точка принадлежит области интегрирования, то есть совпадает с одним из узлов элемента, то интегралы в (3.31) становятся сингулярными. В этом случае коэффициенты в левой части уравнений, содержащие интегралы, равны нулю, так как Hik = 0. Сингулярные интегралы в правой части (3.31) можно вычислить по специальным формулам численного интегрирования, полученным Пине и др.
В случае, если элементы имеют прямоугольную форму, то для вычисления сингулярных интегралов в правой части (3.31) можно использовать аналитические формулы [20, 21] (рис. 3.4):
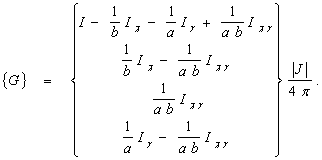(3.33)
где
,
,
.
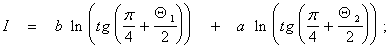
Индексами при координатах здесь обозначены номера узлов (см. рис. 3.4).
При вычислении сингулярных интегралов может дать удовлетворительный результат и применение квадратурной формулы Гаусса (3.32), если взять достаточно большое число точек интегрирования.