Научная электронная библиотека

Монографии, изданные в издательстве Российской Академии Естествознания

Прикладные задачи динамики ледяного покрова

Козин В. М., Жесткая В. Д., Погорелова А. В., Чижиумов С. Д., Джабраилов М. Р., Морозов В. С., Кустов А. Н.,

3.2.3. Конденсация узловых неизвестных

Рассмотрим матричное уравнение МГЭ (3.24) для случая, когда граница исследуемой области состоит из двух частей: Гs - поверхность движущегося судна; Гw - свободная поверхность или поверхность ледяного покрова:

(3.34)

Перепишем уравнение (3.34) по блокам:

.

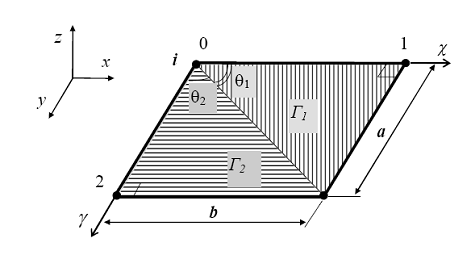
Рис. 3.4. Прямоугольный граничный элемент

.

Из первого уравнения исключим значения потенциалов скоростей на поверхности судна {φ_s}:

.

В результате получим следующее матричное уравнение:

(3.35)

где ,

,

.

В этом уравнении неизвестны векторы {φ_w} и {υ_w}, а вектор известен, так как задано движение судна. Далее уравнение (3.35) необходимо дополнить условием на поверхности Г_w.

Следует заметить, что для плоской границы Г_w матрица [H_ss] является диагональной и легко обращается.