Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
Прикладные задачи динамики ледяного покрова
Козин В. М., Жесткая В. Д., Погорелова А. В., Чижиумов С. Д., Джабраилов М. Р., Морозов В. С., Кустов А. Н.,
3.2.4. Моделирование гидродинамических нагрузок
Рассмотрим применение МГЭ при анализе гидродинамики подводного объекта вблизи свободной поверхности и твёрдого экрана.
Движение под свободной поверхностью.
Пусть подводное судно движется под свободной поверхностью. Примем допущение о малости вызванных движением судна волн, совмещая границу Гw со свободной невозмущенной поверхностью. В этом случае условие на Гw имеет вид
(3.36)
где υw - нормальная скорость движения точек свободной поверхности.
Если рассматривается движение из состояния покоя, то положим
при t = 0 , (3.37)
при t = 0 . (3.38)
Заменим условие (3.36) конечно-разностной моделью. Тогда все вычисления будут представлять собой шаговый по времени процесс. Алгоритм решения задачи состоит из следующих этапов.
1. Из решения уравнения (3.35) находим вектор
при 
, учитывая начальное условие (3.37).
2. Из условия (3.36) определяем 
в узлах свободной поверхности. При этом переносим полученные значения в момент времени 
на момент 
, то есть приближенно считаем, что за малый промежуток времени 
значения не изменяются.
3. Вычисляем значения потенциалов скоростей 
в узлах свободной поверхности (индекс w далее опустим, нижний индекс означает номер временного шага). При этом используем конечные разности «назад» и учитываем начальные условия (3.37) и (3.38):
.
Далее повторяем действия 1 - 3, изменяя значение времени в каждом цикле на 
. С учетом начальных условий формулы для вычисления 
и
принимают вид:
на втором шаге:
;
;
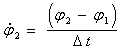на третьем шаге:
;
;
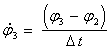на последующих шагах: 
;
.
Аппликаты точек на возмущенной свободной поверхности можно на каждом шаге вычислить, используя интеграл Лагранжа (3.7), пренебрегая квадратами вызванных движением скоростей и учитывая, что избыточные давления на свободной поверхности равны нулю:
.
Давления жидкости на смоченной поверхности судна можно определить по формуле (3.8). Сила волнового сопротивления определяется интегрированием проекций давлений на ось x по смоченной поверхности судна.
Движение вдоль твёрдого экрана.
В этом случае, в отличие от задачи со свободной поверхностью, вместо граничного условия (3.36) вводится условие (3.6)
.
Подставим это условие в уравнения модели МГЭ (3.35):
, (3.39)
. (3.40)
Давления на поверхности Гs и Гw можно вычислить по формуле (3.8).