
Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания

Прикладные задачи динамики ледяного покрова
Козин В. М., Жесткая В. Д., Погорелова А. В., Чижиумов С. Д., Джабраилов М. Р., Морозов В. С., Кустов А. Н.,
3.3.1. Матрица жёсткости конечного элемента пластины на упругом основании
Построим численную модель изгиба ледяной пластины на основе метода конечных элементов (МКЭ). Рассмотрим изопараметрический конечный элемент в форме произвольного четырёхугольника [86] с четырьмя узлами и линейной аппроксимацией параметров, аналогичный граничному элементу, описанному в подразделе 3.2.2 (рис. 3.2).
В каждом узле такие КЭ имеют 3 степени свободы: W - нормальные перемещения; Ax и Ay - углы поворота. Перемещения (прогибы w, углы поворота αx и αy) и координаты точек (x и y) e-го элемента задаются одинаковыми базисными функциями (3.25):
![]() ;
;![]() ;
;
![]() ;
;![]() ;
;
![]() ;
;![]() ;
;
![]() ;
;![]() ;
;
![]() ;
;![]() . (3.41)
. (3.41)
Деформации в плоскости элемента {ε*} и деформации поперечного сдвига {ε°} в узле r (r = 1, 2, 3, 4) выражаются через узловые перемещения следующим образом [86]:
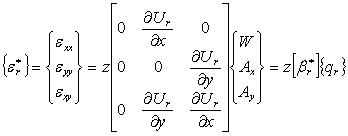 (3.42)
(3.42)
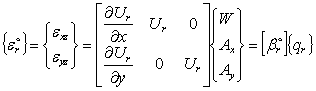 . (3.43)
. (3.43)
Производные в формулах (3.42) и (3.43) определяются в виде:
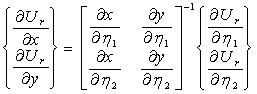 ,
,
где
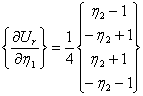 ;
;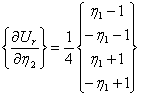 ;
;
![]()
![]()
![]()
![]() .
.
Напряжения в пластине связаны с деформациями законом Гука:
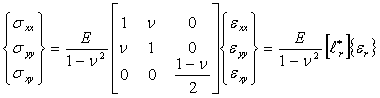 (3.44)
(3.44)
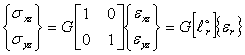 (3.45)
(3.45)
Используя формулы (3.42) – (3.45) при рассмотрении потенциальной энергии деформации конечного элемента, учитывая также влияние гидростатических сил, можно получить выражения для матрицы жёсткости элемента:
 , (3.46)
, (3.46)
где![]() ; r = 1, 2, 3, 4; s = 1, 2, 3, 4; (3.47)
; r = 1, 2, 3, 4; s = 1, 2, 3, 4; (3.47)
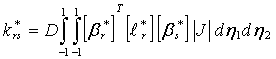 ; (3.48)
; (3.48)
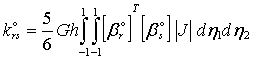 ; (3.49)
; (3.49)
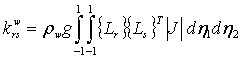 ; (3.50)
; (3.50)
![]() ;
;
D – цилиндрическая жёсткость; G – модуль сдвига; h – толщина пластины. Здесь предполагается, что в пределах конечного элемента его толщина не изменяется. Выражения (3.28) – (3.30) для якобиана преобразования координат ![]() в случае плоской горизонтальной пластины упрощаются:
в случае плоской горизонтальной пластины упрощаются: ![]() .
.