Научная электронная библиотека

Монографии, изданные в издательстве Российской Академии Естествознания

Прикладные задачи динамики ледяного покрова

Козин В. М., Жесткая В. Д., Погорелова А. В., Чижиумов С. Д., Джабраилов М. Р., Морозов В. С., Кустов А. Н.,

3.3.2. Матрица жёсткости полубесконечного элемента

При расчёте изгиба сплошного ледяного покрова методом конечных элементов неизбежна погрешность моделирования, связанная с тем, что ледяной бесконечный покров приближённо заменяется ограниченной пластиной. Эту погрешность можно уменьшить, отдалив границы расчётной сетки от источника нагружения, однако при этом неизбежно увеличивается число элементов, а значит и вычислительные затраты. При решении гидроупругой задачи на однопроцессорном компьютере время счёта может оказаться чрезмерно большим.

.

В связи с этим рассмотрим далее вопрос учета бесконечной протяженности ледяной пластины в одном или нескольких направлениях.

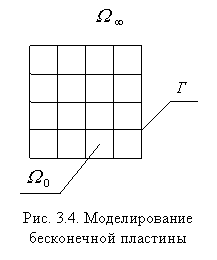
Пластину с бесконечными границами можно представить состоящей из двух областей: конечной Ω₀ и бесконечной Ω_∞ (рис. 3.4). В области Ω₀ пластину будем моделировать рассмотренными ранее конечными элементами.

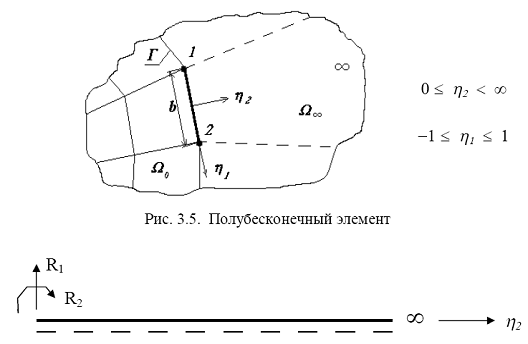
Для того, чтобы учесть влияние бесконечной части пластины Ω_∞ введем на границе Г так называемые полубесконечные элементы (рис. 3.5).

Для этого вначале рассмотрим дифференциальное уравнение изгиба балки - полоски единичной ширины в направлении h₁ и полубесконечной по направлению h₂ от границы Г (рис. 3.6):

.

с граничными условиями:

..

Решение этой задачи известно [105]:

(3.51)

где- функции Клишевича [105];

В точке h₂ = 0 получим

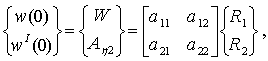
или(3.52)

где

Уравнение (3.52) можно преобразовать к виду

.

где элементы матрицы жесткости определяются так

.

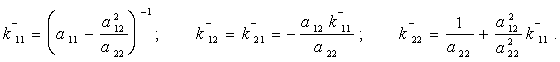Таким образом, перемещения в области Ω_∞ (по направлению h₂ ) аналитически определяются через “узловые” значения усилий или перемещений на границе Г по формулам (3.51) или (3.52).

По ширине полубесконечного элемента пластины (по направлению h₁) принимаются линейные базисные функции

.

Рис. 3.6. Полубесконечная балка - полоска

В результате получена матрица жесткости элемента:

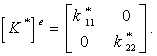(3.53)

Блоки k_rr^* ( r = 1, 2 - номера узлов элемента) определяются в виде

.

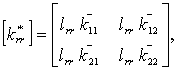где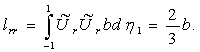

Для перехода от обобщенных узловых перемещений W_r и A_η2r (r = 1, 2) к перемещениям W_r , A_xr и A_yr следует матрицу жесткости (3.53) преобразовать к виду

.

где [T ] - матрица преобразования координат.

Полученные элементы тестировались при решении задачи об изгибе пластины на упругом основании, изображенной на рис. 3.7. Пластина жестко заделана на кромках x = 0 , y = 0. По ширине она разделена на 5 элементов. По длине принято разное количество конечных элементов: 5; 6; 7; 8. В одном из вариантов по ширине имеется 5 конечных и 1 полубесконечный элементы. Все конечные элементы имеют одинаковые размеры (5 х 5 см).

В точке Р пластины приложена сосредоточенная сила. На рис. 3.8 показана относительная разница значений прогибов в точке А при разной дискретизации пластины по отношению к варианту с полубесконечными элементами на линии x = 25 см.