Научная электронная библиотека

Монографии, изданные в издательстве Российской Академии Естествознания

Прикладные задачи динамики ледяного покрова

Козин В. М., Жесткая В. Д., Погорелова А. В., Чижиумов С. Д., Джабраилов М. Р., Морозов В. С., Кустов А. Н.,

3.4.1. Гидродинамические силы

При численном решении задачи гидродинамики по МГЭ, давления воды на поверхность ледяного покрова представляются вектором их значений в узловых точках , которые могут быть получены по формуле (3.8):

. (3.58)

Производная по времени вычисляется с использованием конечных разностей.

Нормальные силы в узлах, действующие на ледяную пластину со стороны жидкости, выражаются через узловые давления с помощью вектора распределения {N}:

(3.59)

Вектор {N} в модели МГЭ формируется путём объединения векторов распределения отдельных элементов. Узловые силы k-го ГЭ определяются в виде:

.

Следовательно, вектор распределения для k-го элемента вычисляется по формуле

.

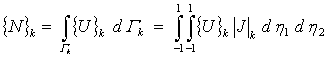Элементы вектора определяются численным интегрированием. В случае прямоугольных элементов размерами a х b получим:

.

При движении ледяного покрова как упругой пластины, на ней должно выполняться граничное условие (3.9), которое в численной модели для узловых значений параметров имеет вид:

, (3.60)

где- нормальные скорости течения в узлах расчётной сетки поверхности пластины; - узловые значения производной от прогиба по времени.

Подставляя (3.60) в уравнения МГЭ (3.35), получим выражение для потенциала скорости на поверхности льда в виде:

.

Далее подставим это выражение в (3.58), а затем в (3.59). В результате гидродинамические силы в узлах пластины будут определяться следующим выражением:

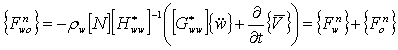. (3.61)

В соответствии с выражением (3.61), гидродинамические инерционные силы на поверхность льда включают две составляющие: 1) от движения подводного судна (как на твёрдую стенку) {F₀ⁿ}; 2) от изгиба пластины {F_wⁿ}:

; (3.62)

. (3.63)

Матрицаопределяет инерцию жидкости при упругих деформациях пластины.

При вычислении сил {F₀ⁿ} производная по времени определяется с применением конечных разностей. Силы {F_wⁿ} зависят от ускорений при деформации пластины. Таким образом, процесс изгиба ледяного покрова от движения подводного судна имеет гидроупругий характер.