Научная электронная библиотека

Монографии, изданные в издательстве Российской Академии Естествознания

Прикладные задачи динамики ледяного покрова

Козин В. М., Жесткая В. Д., Погорелова А. В., Чижиумов С. Д., Джабраилов М. Р., Морозов В. С., Кустов А. Н.,

3.4.2. Общая система обыкновенных дифференциальных уравнений МКЭ и её численное решение

На основе конечноэлементной аппроксимации упругих перемещений пластины в уравнениях (3.2), (3.10) или (3.11) получаются уравнения движения конечных элементов. Обобщённые перемещения каждого узла k в модели МКЭ определяются нормальным смещением и углами поворота относительно осей x и y:

.

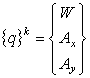Переходя к этим обобщённым перемещениям, гидродинамические силы в каждом узле k сетки конечных элементов будут определяться в виде:

, .

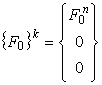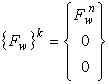Используя стандартные способы сборки общей системы уравнений МКЭ на основе условий совместности перемещений в узлах конечных элементов, получим систему уравнений движения пластины в виде

, (3.64)

где [K] = [K^*] + [K°] + [K^w] - матрица жёсткости пластины, включающая матрицы, определяющие жёсткости в плоскости пластины, от поперечного сдвига и от упругого основания (от гидростатических сил); [С] = t [K] - матрица коэффициентов внутреннего сопротивления; [M] = [M°] + [m] - матрица масс, включающая коэффициенты инерции упругой пластины и прилегающей жидкости.

Задача Коши для системы обыкновенных дифференциальных уравнений (3.64) включает начальные условия. Для скоростейи ускорений можно принять нулевые стартовые значения. Если необходим анализ движения при заданной постоянной скорости подводного судна v, то начальными условиями для перемещений удобнее всего принять перемещения, полученные из предварительного решения статической задачи:

. (3.65)

При этом гидродинамическая нагрузка {F₀} вычисляется для скорости судна v.

В случае моделирования движения судна из состояния покоя, начальные перемещения {q} принимаются равными нулю.

Прямое интегрирование уравнений движения (3.64) выполним по конечно-разностной схеме, изложенной в [37] и дополненной учётом сил демпфирования. Суть этой процедуры состоит в предположении, что за один временной шаг Δt вариация ускоренийизменяется линейно. Используя это допущение, имеем

,

, (3.66)

где n – номер шага по времени.

В уравнение (3.64) для шага n +1

.

подставим формулы (3.66). В результате получим систему, из которой определяются ускорения:

, (3.67)

где ,

,

.

Процедура вычислений включает следующую последовательность действий:

1) по начальным значениям {q},и определяются векторы {b}_n и {d}_n в момент времени n = 1;

2) из уравнения (3.67) вычисляются ускоренияв следующий момент времени n +1; 3) по формулам (3.66) вычисляются перемещения и скорости в момент времени n +1.

Для последующих моментов времени процедура повторяется.