
Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания

Прикладные задачи динамики ледяного покрова
Козин В. М., Жесткая В. Д., Погорелова А. В., Чижиумов С. Д., Джабраилов М. Р., Морозов В. С., Кустов А. Н.,
3.5.1. Течение под ледяным покровом в присутствии подводного объекта или неровности поверхности льда
Рассмотрим тестовую задачу о плоском течении между двумя твёрдыми стенками, одна из которых имеет выступ в виде кругового полуцилиндра (рис. 3.9)[1]. На удалении от препятствия поле скоростей однородное (Vx = 1 м/с). Расстояние между стенками равно 5 м.
Однородный поток на удалении от выступа может моделировать естественное течение или поле скоростей, вызванное движением подводного объекта, размеры которого существенно больше размеров препятствия. Такая задача может быть практически интересна при исследовании возможности разрушения ледового покрова на реке (канале) поперечным препятствием – естественным (перекатом) или искусственным. Препятствие может моделировать также относительно небольшой поперечный выступ на верхней части корпуса движущегося подводного объекта. Можно использовать эту задачу в другой интерпретации, изменив направление вертикальной оси координат. Препятствие можно считать подводной неровностью ледяного покрова, обтекаемой потоком.
 .
.
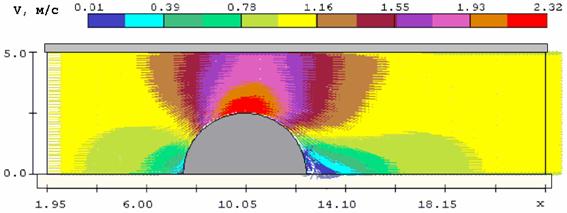
Рис. 3.9. Течение вокруг цилиндрического препятствия
Поток ограничен твёрдыми поверхностями, одна из которых моделирует ледовый покров, то есть влиянием деформации льда на гидродинамическое поле пренебрегается. Вязкость жидкости учитывается, однако анализ течений показывает, что её влияние на поле давлений по поверхности ледяного поля не является существенным.
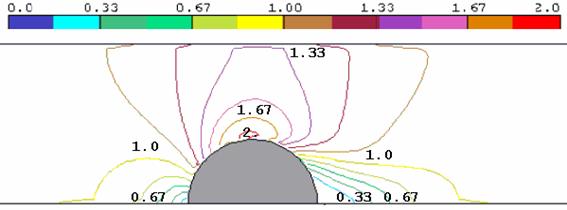
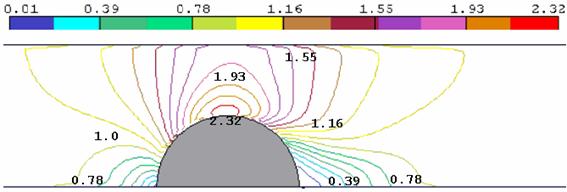
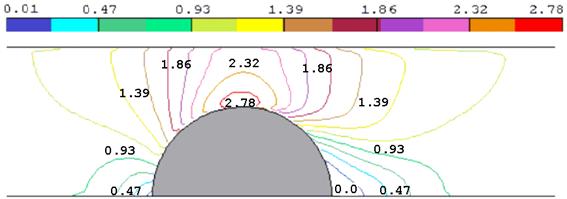
На рис. 3.10 – 3.15 представлены поля скоростей и давлений для течений с радиусом цилиндра R от 2 до 3 м. На рис. 3.16 – 3.17 даны распределения скоростей и давлений по продольному сечению стенки без выступа.
 .
.
Рис. 3.10. Поле скоростей (м/с) при R = 2 м
 .
.
Рис. 3.11. Поле скоростей (м/с) при R = 2.5 м
 .
.
Рис. 3.12. Поле скоростей (м/с) при R = 3 м
 .
.
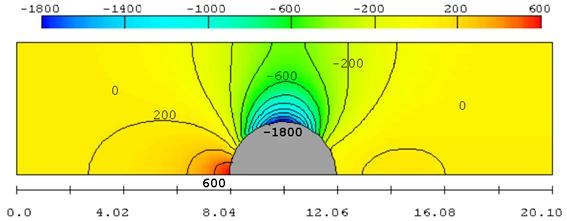
Рис. 3.13. Поле давлений (Па) при R = 2 м
 .
.
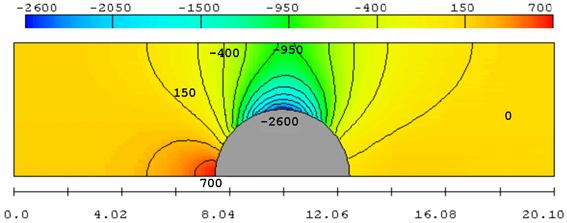
Рис. 3.14. Поле давлений (Па) при R = 2.5 м
 .
.
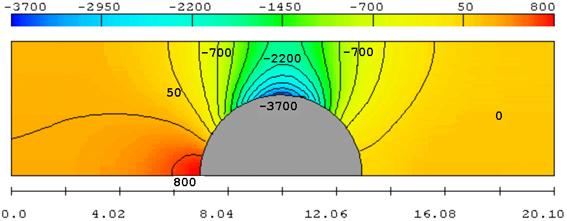
Рис. 3.15. Поле давлений (Па) при R = 3 м
 .
.
Рис. 3.16. Продольные скорости у плоской стенки
 .
.
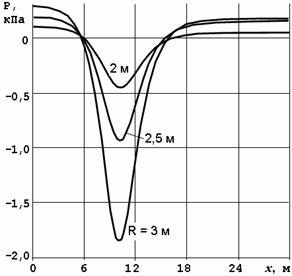
Рис. 3.17. Давления на плоскую стенку
На рисунках видно, что короткое препятствие (цилиндр) на пути потока образует зону пониженного давления на верхней кромке цилиндра. Вызванное течением понижение давления затухает по мере удаления от цилиндра, но остаются существенными на противоположной стенке над препятствием. Если одна из стенок моделирует ледяной покров, то эффект «притягивания» неизбежно вызовет его прогиб. Нагрузка на лёд тем значительнее, чем меньше пространство между выступом и противоположной стенкой.
На стенке с выступом перепад давлений значительно больше, чем на плоской стенке. Отсюда следует, существенного возрастания нагрузки на ледяной покров следует ожидать при наличии подводных выступов льда. Очевидно, что в этих случаях будут присутствовать также концентрации напряжений во льду. Таким образом, наличие торосов, особенно в подводной части, способствует разрушению ледяного покрова гидродинамическими нагрузками.
 .
.
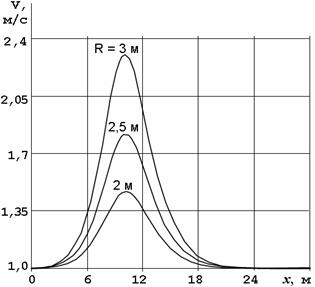
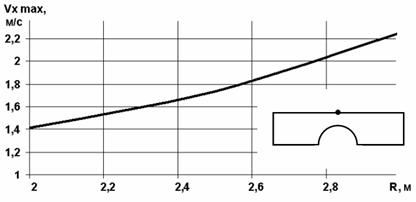
Рис. 3.18. Зависимость продольных скоростей на плоской стенке от размера препятствия
 .
.
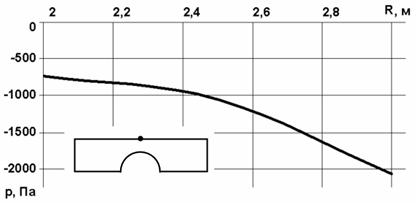
Рис. 3.19. Зависимость давлений на плоской стенке от размера препятствия
На рис. 3.18 – 3.20 представлено влияние размеров цилиндра на вызванные течением скорости и давления.
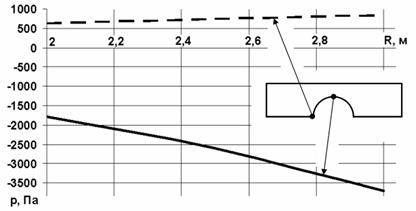
Рис.3.20. Зависимость давлений на поверхности препятствия от его размера