Научная электронная библиотека

Монографии, изданные в издательстве Российской Академии Естествознания

Прикладные задачи динамики ледяного покрова

Козин В. М., Жесткая В. Д., Погорелова А. В., Чижиумов С. Д., Джабраилов М. Р., Морозов В. С., Кустов А. Н.,

3.6.1. Изгиб однородного ледяного покрова от движения ПЛ без рубки

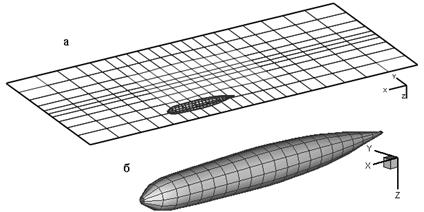
Рассмотрим вначале пример расчёта трёхмерного стационарного течения при движении ПЛ пр. 971 без учёта влияния рубки вблизи поверхности воды и ледяного покрова [87]. Поверхность корабля и часть расположенной над ним поверхности воды была разделена нерегулярной сеткой на четырёхугольные ГЭ с линейной аппроксимацией функций потенциала и скорости (рис. 3.39). На поверхности ПЛ было 252 узла (21 поперечное сечение по 12 узлов), а на поверхности воды – 253 узла (23 поперечных сечения по 11 узлов). Длина и полуширина расчётной сетки на поверхности воды составляла соответственно 300 и 60 м.

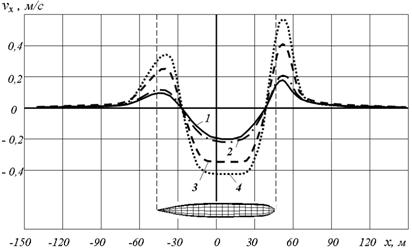
На поверхности воды для разных вариантов расчётов принимались условия свободной (3.36) и жёсткой (3.6) границы. На рис. 3.40 приведено распределение вызванных движением корабля касательных скоростей на поверхности воды в диаметральной плоскости. Из рисунка видно, что чем ближе ПЛ к свободной поверхности, тем более чётко выражены носовой и кормовой источники волнообразования, между которыми наблюдается примерно равномерная по длине область понижения уровня.

Результаты численных экспериментов показали, что размеры учитываемой в модели сетки по поверхности воды достаточны. Как к продольным, так и к поперечным краям сетки возмущения практически полностью затухали (рис. 3.41).

Расчёты профиля волн в модели со свободной поверхностью воды в рассмотренной выше стационарной постановке следует воспринимать лишь как первое приближение, приближающееся к реальности лишь при малых числах Фруда. Тем не менее, в сопоставительном плане результаты могут иметь практическое значение.

.

Рис. 3.39. Расчётная модель движения ПЛ: а) дискретизация свободной поверхности; б) дискретизация судна

.

Рис. 3.40. Вызванные движением ПЛ скорости на поверхности воды: 1 – Н = 0,1L «подольдом»; под свободной поверхностью: 2- Н = 0,1L; 3- Н = 0,05L; 4- Н = 0,03L

.

Сплошной лед представлялся в виде упругой пластины бесконечной протяжённости, лежащей на упругом основании. Толщина льда считалась постоянной. Область и степень дискретизации пластины ограничены условиями минимума вычислительных затрат и достаточной точности расчётов. Края такой искусственно ограниченной пластины оставлены свободными.

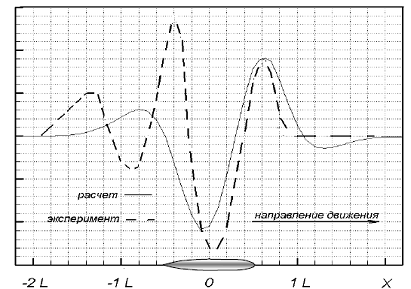
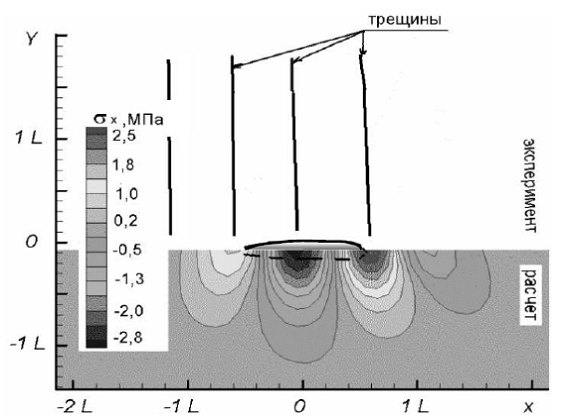
Расчёты включали два этапа: на первом по МГЭ определялись давления на лёд в предположении его жёстким; на втором этапе вычислялись прогибы и напряжения во льду по МКЭ. Некоторые результаты расчётов сопоставлялись с данными, полученными из физических экспериментов [67, 88]. На рис. 3.42 – 3.43 показаны прогибы и положения трещин при разрушении льда в эксперименте, а также прогибы и изгибные напряжения, полученные расчётом [87].

.

Рис. 3.42. Сопоставление перемещений льда по неразрушаемой (расчёт) и разрушаемой (эксперимент) моделям ледяного покрова

.

Рис. 3.43. Сопоставление расчётных изгибных напряжений с разрушениями в модельном льду

Разница в результатах расчёта и эксперимента на рис. 3.42 объяснятся тем, что при разрушении сплошность модельного льда нарушалась, вследствие чего амплитуды прогибов в кормовой части возрастали, а расстояния между крайними точками профиля сокращались. Теоретический уровень изгибных напряжений в ледяной пластине (рис. 3.43) существенно превосходил предел прочности модельного льда на изгиб.

Следует отметить факт удовлетворительного соответствия теоретического уровня изгибных напряжений в ледяной пластине с расположением трещин в модельном льду на рис. 3.43. Таким образом, по результатам расчета изгибных напряжений в неразрушаемом льду можно прогнозировать трещинообразование в ледяном покрове.