Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
Прикладные задачи динамики ледяного покрова
Козин В. М., Жесткая В. Д., Погорелова А. В., Чижиумов С. Д., Джабраилов М. Р., Морозов В. С., Кустов А. Н.,
4.1.1. Математическая модель задачи
Расчетная схема задачи показана на рис. 4.1. При решении задачи примем прямоугольную систему координат, расположив оси x и y в плоскости ледяной пластины, а ось z направив вверх (см. рис. 4.1).
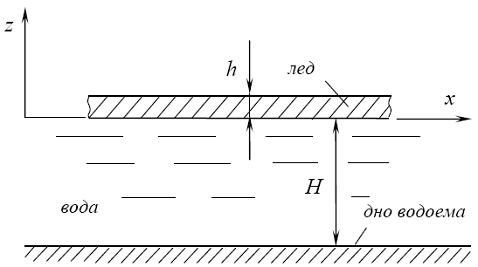
Основным дифференциальным уравнением задачи является уравнение Лапласа для потенциала скорости движения жидкости F
Решение уравнения (4.1) должно удовлетворять ряду граничных условий.
Одним из них является дифференциальное уравнение колебаний ледяного покрова [124], представляющее собой динамическое граничное условие на поверхности соприкосновения льда и воды.
.
Рис. 4.1. Ледяная пластина (расчетная схема)
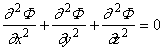(4.1)
Если лед рассматривается как упругий изотропный материал, то есть для него считается справедливым закон Гука
,
то дифференциальным уравнением колебаний будет
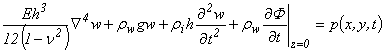(4.2)
где w - прогиб льда, rw - плотность воды, ri - плотность льда, g - ускорение свободного падения, h - толщина льда, p - интенсивность внешней нагрузки, E – модуль Юнга, n - коэффициент Пуассона, t - время.
Кроме дифференциального уравнения колебаний ледяного покрова, должны также удовлетворяться граничные условия на дне водоема и на границе льда и воды
(4.3)
(4.4)
Согласно методу конечных элементов, при решении задачи рассматривается ограниченная в горизонтальной плоскости, но достаточно большая область ледяного покрова и находящаяся под ней жидкость. Размер этой области должен быть достаточным для того, чтобы можно было считать, что на ее границе Г перемещения пластины уже практически отсутствуют, и принять условия жесткой заделки
,
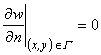, (4.5)
где n – нормаль к Г.
Аналогично, на вертикальной поверхности, ограничивающей жидкость под ледяным покровом, примем условие непротекания [38]
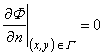(4.6)
где нормаль n перпендикулярна оси z.
Уравнение (4.2) составлено без учета сил сопротивления движению ледяного покрова. Однако при изучении воздействия на ледяной покров как стационарной, так и движущейся нагрузки было замечено, что для более полного соответствия реальных деформаций ледяного покрова их расчетным значениям необходим учет внутреннего сопротивления льда.