Научная электронная библиотека

Монографии, изданные в издательстве Российской Академии Естествознания

Прикладные задачи динамики ледяного покрова

Козин В. М., Жесткая В. Д., Погорелова А. В., Чижиумов С. Д., Джабраилов М. Р., Морозов В. С., Кустов А. Н.,

4.1.2. Дифференциальное уравнение колебаний ледяного покрова при учете внутреннего сопротивления льда

Наиболее часто применяемыми реологическими моделями, позволяющими учитывать внутреннее сопротивление, являются модели Кельвина-Фойгта и Максвелла [111].

Модель Кельвина-Фойгта представляет собой параллельное соединение упругого и вязкого элементов. В этом случае напряжение s связано с деформацией e зависимостью

(4.7)

где E – модуль упругости, h - коэффициент вязкости.

При учете внутреннего сопротивления льда в соответствии с (4.7) дифференциальное уравнение колебаний ледяной пластины примет вид

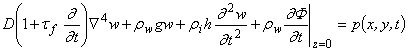(4.8)

где - время релаксации.

Модель Максвелла представляет собой последовательное соединение упругого и вязкого элементов. В этом случае напряжение s и деформация e связаны между собой зависимостью

(4.9)

а дифференциальное уравнение колебаний ледяного покрова, соответствующее (4.9), имеет вид

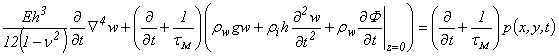(4.10)

где введено обозначение .