Научная электронная библиотека

Монографии, изданные в издательстве Российской Академии Естествознания

Прикладные задачи динамики ледяного покрова

Козин В. М., Жесткая В. Д., Погорелова А. В., Чижиумов С. Д., Джабраилов М. Р., Морозов В. С., Кустов А. Н.,

4.1.3. Исключение функции потенциала скорости движения жидкости

Представим прогиб w и потенциал F в виде сумм некоторого числа n отдельных слагаемых [38, 40]:

(4.11)

(4.12)

Если внутреннее сопротивление льда не учитывается, то математическую модель задачи составляют уравнения (4.1) - (4.6).

В случае принятия модели Кельвина-Фойгта уравнение (4.2) заменяется уравнением (4.8). Подставим (4.11) и (4.12) в уравнения (4.1), (4.3), (4.4), (4.8). При этом уравнение (4.3) удовлетворяется, а уравнения (4.1), (4.4), (4.8) преобразуются к виду

(4.13)

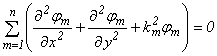, (4.14)

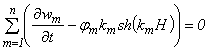, (4.15)

где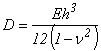- цилиндрическая жесткость пластины.

Исключая из (4.13), (4.14), (4.15) j_m, получим систему двух уравнений

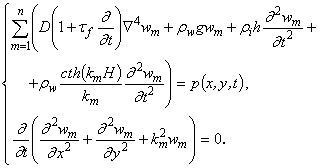(4.16)

В случае принятия модели Максвелла уравнение (4.2) следует заменить уравнением (4.10). Внеся (4.11) и (4.12) в уравнения (4.1), (4.3), (4.4), (4.10) и исключив из полученных уравнений j_m, придем к системе уравнений

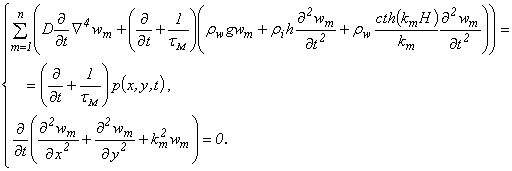(4.17)

Если водоем ограничен вертикальными стенками, то следует рассмотреть еще условие непротекания на стенке (4.6). Из (4.4), (4.6), (4.11) и (4.12) получим

,

,

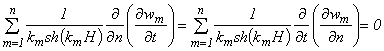откуда следует, что на границе водоема должно выполняться условие

.