
Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания

Прикладные задачи динамики ледяного покрова
Козин В. М., Жесткая В. Д., Погорелова А. В., Чижиумов С. Д., Джабраилов М. Р., Морозов В. С., Кустов А. Н.,
4.1.4. Система матричных дифференциальных уравнений задачи
Используя алгоритм метода конечных элементов, построим дискретную модель ледяной пластины и положим, что
![]() (4.18)
(4.18)
где Ni(x,y) - функции формы [108], qim(t) - компоненты вектора узловых перемещений [q]m(t):
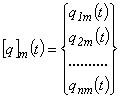 (4.19)
(4.19)
n - число узловых перемещений (тот же смысл эта величина имеет и в формулах (4.11), (4.12)). Значение n связано с типом и количеством конечных элементов, образующих дискретную модель ледяной пластины. Необходимое для достижения достаточной точности число конечных элементов оценивается отдельно для каждой конкретной задачи.
Прогиб пластины
![]() (4.20)
(4.20)
где![]() .
.
Величины qi(t) являются компонентами полного вектора узловых перемещений [q](t):
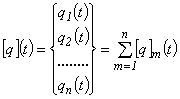 ,
,
где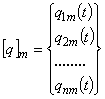 .
.
Для получения разрешающей системы уравнений задачи в случае использования модели Кельвина-Фойгта внесем в систему (4.16) прогиб в форме (4.18) и применим к получившимся уравнениям обобщенный метод Бубнова-Галеркина. В результате придем к системе двух матричных уравнений
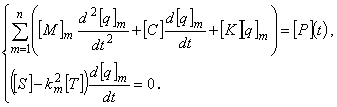 (4.21)
(4.21)
В случае принятия модели Максвелла исходные зависимости задачи аналогичным образом сводятся к системе двух матричных уравнений
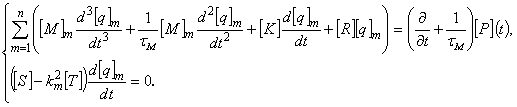 (4.22)
(4.22)
Элементы матриц, входящих в (4.21) и (4.22), зависят от физико-механических параметров задачи и от вида функций формы конечных элементов, а [P](t) - это вектор внешних узловых нагрузок, компоненты которого определяются по формуле
![]() .
.