Научная электронная библиотека

Прикладные задачи динамики ледяного покрова

Козин В. М., Жесткая В. Д., Погорелова А. В., Чижиумов С. Д., Джабраилов М. Р., Морозов В. С., Кустов А. Н.,

4.1.5. Решение системы матричных дифференциальных уравнении задачи

Для решения систем (4.21) и (4.22) применим метод конечных разностей. Разобьем рассматриваемый промежуток времени на L равных участков; первую, вторую и третью производные в r-м узле сетки времени аппроксимируем разностными формулами

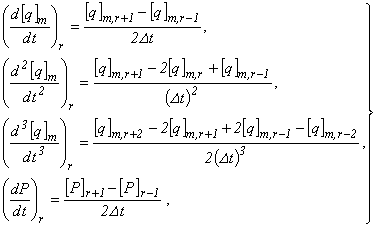(4.23)

где Dt - шаг сетки, [q]_m,r и [P]_r - значение векторов [q]_m и [P]в r-м узле.

Подстановка (4.23) в систему (4.21) приводит к матричным уравнениям в конечных разностях

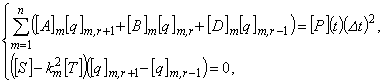(4.24)

r = 0,1,2,...,L ,

где , , .

Аналогично, из (4.22) и (4.23) получим

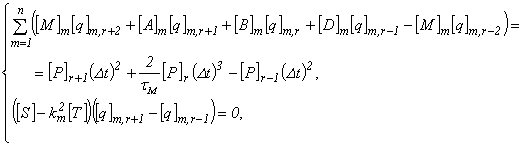(4.25)

r = 0,1,2,...,L ,

где, ,.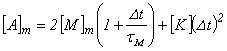

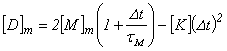Второму уравнению систем (4.24) и (4.25) можно удовлетворить, представив [q]_m,r в виде

(4.26)

где [X]_m - собственный вектор в случае однородного уравнения с матрицей , соответствующий собственному значению , a_m,r - неизвестный коэффициент. Определение [X]_m иявляется первым шагом решения задачи.

Подставив (4.26) в первые уравнения систем (4.24) и (4.25), а также в начальные условия задачи, получим в каждом из этих случаев систему уравнений для определения a_m,r . Найдя a_m,r , вычислим узловые перемещения в узле сетки времени

(4.27)

Начальные условия в случае использования модели Кельвина-Фойгта примем в виде , . При использовании модели Максвелла добавим к этим условиям еще два: , . Функции , , ,считаются известными.