Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
Прикладные задачи динамики ледяного покрова
Козин В. М., Жесткая В. Д., Погорелова А. В., Чижиумов С. Д., Джабраилов М. Р., Морозов В. С., Кустов А. Н.,
4.1.6. Определение напряжений в точках ледяной пластины
При использовании реологической модели Кельвина-Фойгта изгибающие и крутящий моменты, действующие в сечениях, нормальных к осям x и y, и приходящиеся на единицу длины сечения, связаны с прогибом пластины зависимостями
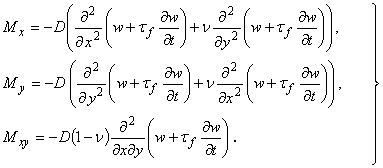(4.28)
Пусть wr – прогиб в r-м узле сетки времени. В соответствии с (4.20)
(4.29)
где 
- i-е узловое перемещение в r-м узле сетки времени, n – число узловых перемещений в общей системе координат.
Построим разностную схему для скорости изменения прогиба в r-м узле временной сетки. На основании (4.29), используя разностную формулу первой производной, получим
(4.30)
Внеся (4.30) в (4.28), получим:
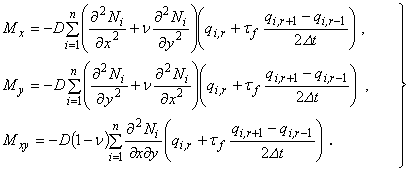(4.31)
При использовании реологической модели Максвелла моменты Mx, My, Mxy связаны с прогибом w зависимостями
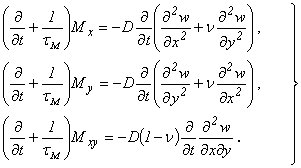(4.32)
Рассмотрим первое уравнение (4.32). Меняя в правой части порядок дифференцирования, можем написать
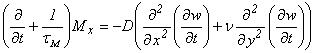(4.33)
Пусть wr - прогиб в r-м узле сетки времени. Тогда из (4.29), (4.30) и (4.33) найдем, что в r-м узле временной сетки
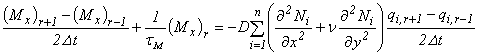(4.34)
Аналогично получим, что
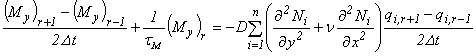(4.35)
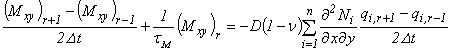(4.36)
Введем обозначение
(4.37)
Выразим из (4.34) – (4.36) значения моментов в (r+1)-м узле временной сетки. С учетом обозначения (4.37) получим
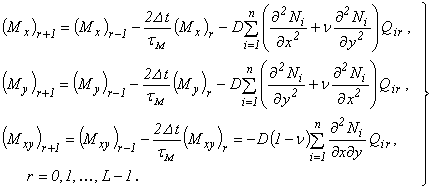(4.38)
Значения моментов при r = 0 и r = -1 являются начальными условиями.
Найдя Мx , My и Mxy по формулам (4.31) или (4.38), вычислим наибольшие нормальные sx max , sy max и наибольшее касательное txy max напряжения. Соответствующие величины для частного случая изотропной пластины обозначим 
,
, 
. Они определяются по формулам
(4.39)