Научная электронная библиотека

Монографии, изданные в издательстве Российской Академии Естествознания

Прикладные задачи динамики ледяного покрова

Козин В. М., Жесткая В. Д., Погорелова А. В., Чижиумов С. Д., Джабраилов М. Р., Морозов В. С., Кустов А. Н.,

4.2. Сопоставление значений прогибов ледяного покрова, полученых с использованием реологических моделей Максвелла и Кельвина-Фойгта

При выборе метода расчета напряженно-деформированного состояния ледяного покрова, находящегося под действием стационарной или движущейся нагрузки, возникает вопрос о том, какая реологическая модель является наиболее подходящей в данном конкретном случае. Существует мнение, что результаты, наиболее отвечающие натурным наблюдениям, при стационарных или медленно изменяющихся воздействиях дает модель Максвеллла, а при быстро протекающих процессах – модель Кельвина-Фойгта. Заметим, что в теории упруго-вязких тел рассматриваются также многоэлементные схемы, содержащие несколько упругих и вязких элементов.

Для сравнения значений прогибов ледяного покрова, полученных при использовании двух упомянутых моделей, была рассмотрена задача о прямолинейном равномерном движении сосредоточенной силы по ледяному покрову постоянной толщины. Глубина водоема считалась постоянной. Расчет прогибов выполнялся численным методом, изложенным выше.

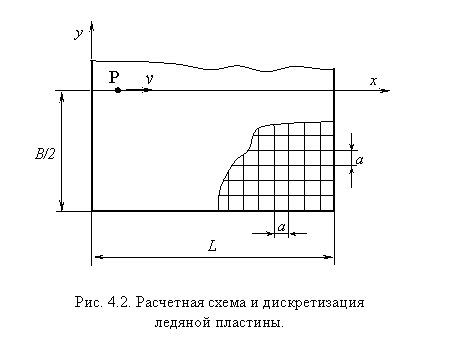
Согласно алгоритму численного метода из ледяного покрова была выделена пластина прямоугольной формы длиной L = 400 м и шириной B = 400 м, размеры которой (одни и те же как при использовании модели Максвелла, так и при использовании модели Кельвина-Фойгта) достаточны для того, чтобы принять на ее контуре условия жесткой заделки. Сила P двигалась по оси симметрии пластины x (рис. 4.2). При расчете учитывалась симметрия пластины и рассматривалась только ее часть при y £ 0. Дискретная модель пластины состояла из квадратных конечных элементов со стороной a = 25 м (см. рис. 4.2).

.

В начальный момент времени сила находилась в покое в точке оси x с координатой x = x_о; пластина имела при этом соответствующий статический прогиб. Из состояния покоя сила начинала движение по оси x, мгновенно приобретая при этом скорость v. Прогибы определялись для момента прохождения силы через центр пластины.

Основные параметры задачи имели следующие значения: P = 0,4×10⁶ Н; E = 0,73×10¹⁰ Пa, что примерно соответствует середине известного диапазона значений модуля Юнга льда; коэффициент Пуассона n = 0,3; плотность льда r_i = 900 кг/м³; плотность воды r_w = 1000 кг/м³; глубина водоема H = 5 м; толщина ледяного покрова h = 0,5 м; время релаксации деформаций t_f = 10 с. Скорость движения силы v варьировалась от 0 до 7 м/с. При v = 1 м/с сила начинала движение от точки x_о = 125 м, при остальных значениях скорости – от точки x_о = 25 м. Шаг сетки времени принимался равным 0,125 с в случае схемы Кельвина-Фойгта и 0,025 – 0,05 с при схеме Максвелла.

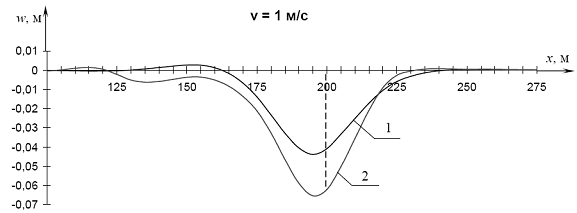
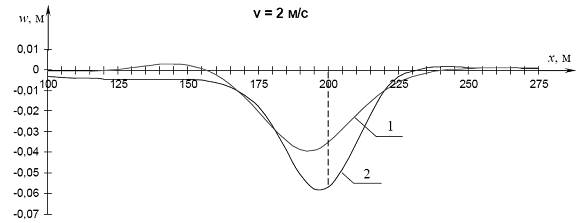
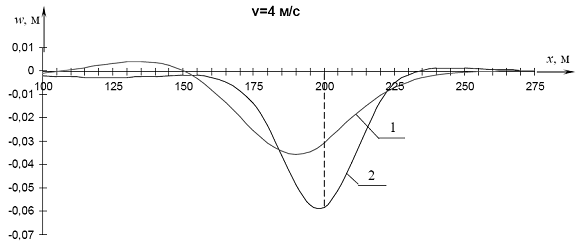
Результаты расчетов прогибов при разных значениях скорости v отражены на рис. 4.3 – 4.6, где даны графики прогибов в точках оси x для ряда значений скорости движения силы.

Для сравнения результатов, к которым приводит применение двух рассматриваемых реологических моделей при определении прогибов ледяного покрова в случае статического нагружения, была рассмотрена задача о действии на ту же пластину статической сосредоточенной силы, приложенной в центре пластины. Расчет прогибов был выполнен аналогично тому, как это делалось при движении нагрузки. При этом точка приложения силы в начальный момент времени совпадала с центром пластины, а значение скорости было принято равным нулю.

.

Рис. 4.3. Графики прогибов при v = 1 м/с: 1 – модель Кельвина-Фойгта; 2 – модель Максвелла

.

Рис. 4.4. Графики прогибов при v = 2 м/с: 1 – модель Кельвина-Фойгта; 2 – модель Максвелла

.

Рис. 4.5. Графики прогибов при v = 4 м/с: 1 – модель Кельвина-Фойгта; 2 – модель Максвелла.

.

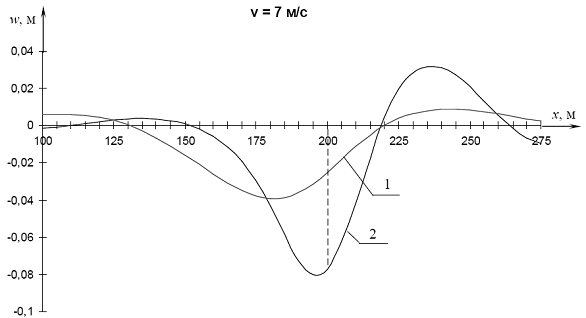
Рис. 4.6. Графики прогибов при v = 7 м/с: 1 – модель Кельвина-Фойгта; 2 – модель Максвелла.

.

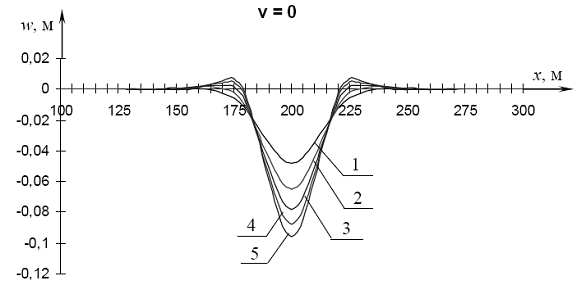
Рис. 4.7. Графики прогибов при v = 0: 1 - t = 0; 2 - t = 10 с; 3 - t = 20 с; 4 - t = 30 с; 5 - t = 40 с

Определение прогибов было выполнено для пяти моментов времени: t = 0, 10, 20, 30, 40 с. На рис. 4.7 даны графики прогибов в точках оси x при каждом из этих значений t. Прогибы, определенные с использованием модели Кельвина-Фойгта, для любого момента времени одни и те же, и их графиком является кривая 1 (см. рис. 4.7). Она же соответствует прогибам при t = 0, полученным, так же как и остальные графики (кривые 2 – 5), с применением модели Максвелла.

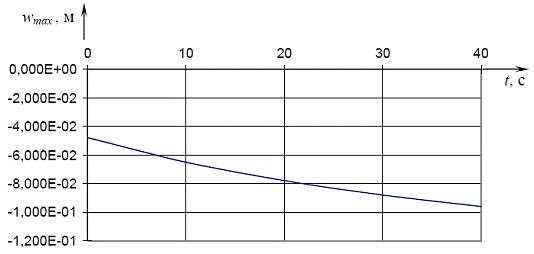
Как видно из графиков на рис. 4.7, с течением времени максимальный прогиб возрастает, то есть наблюдается ползучесть льда. Зависимость максимального прогиба от времени действия силы дана на рис. 4.8. График на рис. 4.8 имеет вид, характерный для кривой ползучести.

.

Рис. 4.8. Зависимость максимального прогиба от времени действия силы

На основании проведенных расчетов можно сделать следующие выводы:

1. При движении нагрузки по льду даже с достаточно малой скоростью (2 и 4 м/с) и тем более с высокой скоростью модель Кельвина-Фойгта позволяет получить более близкую к действительности форму изгиба ледяного покрова, чем модель Максвелла. Это подтверждается сравнением полученных графиков прогибов с результатами натурных экспериментов И.С.Песчанского [89] и Т.Такизавы [160]. Более высокие полученные расчетом по Максвеллу значения прогибов (см. рис. 4.3 – 4.6) объясняются тем, что эта модель предусматривает накопление с течением времени пластических деформаций, чего на практике при движении нагрузки по льду не наблюдается.

2. При статическом приложении нагрузки модель Кельвина-Фойгта не позволяет учесть ползучесть льда, наличие которой было замечено на практике. В этом случае может быть оправданным применение модели Максвелла, которая дает возможность отразить этот эффект (см. рис. 4.7, 4.8).