Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
Прикладные задачи динамики ледяного покрова
Козин В. М., Жесткая В. Д., Погорелова А. В., Чижиумов С. Д., Джабраилов М. Р., Морозов В. С., Кустов А. Н.,
4.3. Численное решение задачи о воздействии ударного импульса на ледяной покров
Исследования напряженно-деформированного состояния ледяного покрова при воздействии на последний динамических нагрузок позволяют решить ряд прикладных проблем ледотехники, возникающих на замерзающих водных путях при эксплуатации гидротехнических и инженерных сооружений на речных и морских акваториях, а также при проведении мероприятий по предотвращению разрушительных наводнений в периоды ледохода и ледостава. В частности, большой интерес представляет вопрос о поведении ледяного покрова после воздействия на него импульсной нагрузки. С такой задачей приходится встречаться при проведении взрывных работ для предотвращения образования заторов и зажоров или для их разрушения.
Имеющиеся в настоящее время аналитические решения этой задачи [62, 124] получены лишь для сравнительно простых ледовых условий. Получение аналитических решений при достаточно сложной, как часто имеет место в реальных условиях, ледовой обстановке (произвольные очертания берегов водоема, переменная глубина водоема, неоднородность ледяного покрова и т.п.) или невозможно, или сопряжено с большими математическими трудностями. В этом плане перспективным представляется использование численного метода, данного в [40] (заметим, что при разработке алгоритма расчета, приведенного в [40], была принята реологическая модель Кельвина-Фойгта).
В качестве примера такого использования рассмотрим задачу по определению прогибов ледяного покрова при воздействии на него точечного ударного импульса, то есть внезапно приложенной силы P, действие которой продолжается в течение промежутка времени Dt, малого по сравнению с периодом собственных колебаний. При решении задачи, следуя [124], ледяной покров рассматривается как пластина, а вода считается идеальной несжимаемой жидкостью. Глубина водоема принимается постоянной.
В данном случае в дифференциальном уравнении колебаний ледяного покрова (4.8) следует принять
,
где U – ударный импульс, d(x,y) и d(t) – дельта-функции Дирака.
Алгоритм решения этой задачи построим аналогично тому, как это было сделано в [40] для другого случая воздействия на ледяной покров – при движении по нему нагрузки.
Если единственным воздействием на ледяной покров является ударная импульсная нагрузка при t = 0, следует прогиб пластины в начальный момент времени и вектор [P] в системе (4.21) принять равными нулю. Фактором, инициирующим движение системы, будет начальная скорость ледяной пластины, которую последняя получит в момент действия импульса.
Определение начальных скоростей точек пластины можно произвести на основе закона сохранения количества движения, согласно которому 
, где K – количество движения пластины, приобретенное в результате удара, 
- импульс силы.
Для решения этой задачи применим метод конечных элементов. В соответствии с ним прогиб пластины аппроксимируется выражением
,
где qi – узловые перемещения, Ni – функции формы, n – число узловых перемещений.
При определении начальных скоростей необходимо задаться законом их зависимости от координат x, y точек пластины. Будем считать, что скорости пропорциональны прогибам в точках пластины при статическом действии на нее сосредоточенной силы P в точке приложения импульса. Тогда распределение скоростей по площади пластины можно выразить формулой
, (4.40)
где 
- скорость пластины в точке удара; 
- статический прогиб пластины от действия силы P; 
- статический прогиб пластины в точке приложения P; xP, yP – координаты точки приложения P. Заметим, что при определении статического прогиба можно принимать P = 1, так как отношение 
не зависит от значения P.
Количество движения пластины теперь можно вычислить по формуле
,
где r - плотность льда; h – толщина ледяного покрова; интеграл берется по площади пластины S.
Обозначив число конечных элементов через m, из предыдущей формулы получим
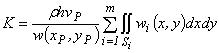, (4.41)
где 
- прогиб i-го конечного элемента; Si – площадь i-го конечного элемента.
Если число узловых перемещений конечного элемента равно ni, то
, (4.42)
где 
- узловые перемещения i-го конечного элемента, 
- его функции формы.
Подставляя (4.42) в (4.41), получим
.
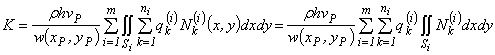Вводя обозначение
,
и учитывая, что K = U, получим следующее равенство для определения vP:
.
Найдя vP, по формуле (4.40) определим линейные скорости точек пластины и, в частности, скорости узлов сетки конечных элементов. Таким образом, будет получен вектор начальных скоростей, входящий в начальные условия задачи.
.
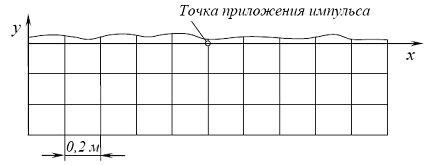
Рис. 4.9. Дискретная модель
В качестве примера приведем результаты предварительного теоретического расчета изложенным выше методом прогибов пластины при модельном эксперименте по исследованию реакции ледяного покрова на действие импульсной нагрузки. Ледяной покров моделируется резиновой пленкой толщиной 1 мм, которая имеет форму прямоугольной пластины длиной L = 2 м и шириной B = 1,2 м. Глубина водоема составляет 0,02 м. В расчет были заложены реальные параметры модели. При дискретизации пластина была разбита на квадратные конечные элементы (рис. 4.9). Значение импульса было принято равным 0,98·10-4 Н·с, точка его приложения находилась в центре пластины, его действие было направлено вверх.
На рис. 4.10 - 4.14 показаны графики прогибов на оси x пластины в разные моменты времени; на каждом графике указано время t, прошедшее с момента приложения импульса до данного момента. По графикам можно проследить развитие процесса деформирования ледяного покрова после приложения импульсной нагрузки.