
Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
СУММАРНЫЕ ВОДНЫЕ РЕСУРСЫ КРУПНЫХ РЕК МИРА (П.М. Мазуркин)
Кумулятивные гидрологические показатели дают возможность определения пределов суммарных водных ресурсов, в частности крпуных рек мира по списку из учебника [1, с.127, табл. 6.1].Суммарная длина всех 16 крупных рек мира (рис. 1) равна
![]()
![]() . (1)
. (1)
Формула (1) имеет коэффициент корреляции 0,999985.
Общая площадь бассейнов водосбора 18 крупных рек (рис. 2) равна
![]()
![]() . (2)
. (2)
До суммирования реки ранжируются по убыванию гидрологического параметра, поэтому в формулах первые числа показывают лидера - Амазонку. Максимальная относительная погрешность (2) 2,75 %.
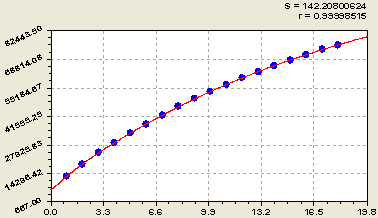
Рис. 1. График кумуляты длины крупных рек мира по формуле (1)
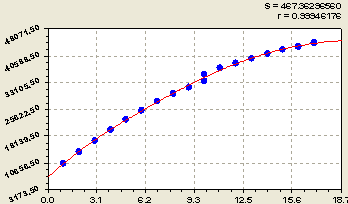
Рис. 2. График кумуляты площади бассейнов у 18 крупных рек мира по формуле (2)
Кумулята расходов воды 18 крупных рек мира по рис. 3 имеет вид
![]()
![]() . (3)
. (3)
На правой стороне графика виден предел роста у расхода воды. Очень малая относительная погрешность 0,26 % позволяет с высоким доверием 100 - 0,26 = 99,74 % сделать вывод о необходимости моделирования по обобщенной формуле
![]()
![]() (4)
(4)
по всему множеству рек мира, в котором крупные великие реки станут основной частью.
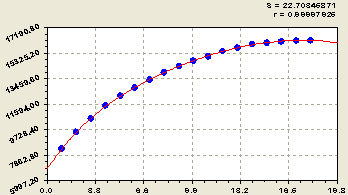
Рис. 3. График кумуляты расходов речной воды у 18 крупных рек мира по формуле (3)
При этом ежегодные модели расходов речной воды можно оценивать по моделям типа (4) для различных территорий, например, для всех рек и их притоков Приволжского федерального округа.
Литература
1. Михайлов, В.Н. Общая гидрология: Учебник / В.Н. Михайлов, А.Д. Добровольский. - М.: Высшая школа, 1991. - 368 с.
