Научная электронная библиотека

Монографии, изданные в издательстве Российской Академии Естествознания

Охрана и защита, обустройство, индикация и тести-рование природной среды. Сборник статей студентов, аспирантов и преподавателей: Научно-учебное издание

Мазуркин П. М.,

РАНГОВОЕ РАСПРЕДЕЛЕНИЕ ПАРАМЕТРОВ ПОЧВЫ (П.М. Мазуркин, С.П. Семенова, магистрант (ЗОС-51))

Параметр - это показатель, характеризующий систему, в нашем случае системой является почва на пойменном лугу.

В статье показаны закономерности рангового распределения семи параметров по экспериментальным данным [4, с.102-103, табл. 22], которые были измерены биологами по методике [1]. Целью такого анализа является проверка добротности данных для моделирования.

Вначале дадим теоретическое обоснование нашему подходу.

Метод массовых наблюдений является основой многих статистических исследований. Статистические данные обрабатываются какими-то способами для того, чтобы найти вероятный детерминизм в массе однородных (или разнородных) наблюдений за некоторым природным или природно-антропогенным явлением или процессом.

Таким образом, в существующих методах биологического изучения явлений и процессов можно выделить три основных аспекта:

во-первых, заранее (априори) до проведения исследований допускается, что существует статистическая закономерность - форма причинной связи между совокупностями явлений, образующих структуру события и процесс поведения объекта исследования чередованием во времени изменяющихся событий, которую множество измеренных состояний объекта исследования определяет не однозначно, а лишь с определенной вероятностью, то есть статистически;

во-вторых, эта статистическая закономерность, по данным о многих состояниях (повторения измерений в один момент времени и/или в различные состояния во времени) поведения объекта исследования, ищется на ПЭВМ в некой программной среде с помощью устойчивых законов распределения (математической модели, построенной из отдельных «узлов и деталей» в виде известных устойчивых законов [3], идентифицируемой по статистическим данным);

в-третьих, по найденной статистическим моделированием на ПЭВМ, в нашем случае в программной среде CurveExpert-1.38, устойчивой конструкции математической модели, выраженной в виде составного алгебраического уравнения, в дальнейшем вычисляются критерии оценки изуачемого явления или процесса, а по значениям параметров будущих состояний объекта судят о прогнозировании.

При этом предполагается, что начальные эвристические условия поведения объекта исследования будут неизменными и в будущем, то есть характер экологического поведения продолжится от периода, охватываемого статистическими данными (основание прогноза), не будет меняться и в период упреждения во времени на будущее, то есть на горизонт прогноза.

К переменным эвристическим условиям можно отнести не только естественные природные изменения, но и различные экологические мероприятия, принимаемые и реализуемые людьми, призванные улучшить в последующем экологическое состояние какой-то территории. Последовательность во времени экологических состояний образует экологический режим, который должен быть управляемым и предсказуемым по естественному поведению природных объектов и всей окружающей природной среды, в частности предсказуемости по последствиям функционирования природных, природно-антропогенных, природно-техногенных или технических объектов.

Для прогнозирования экологического режима и управления природно-техногенными системами необходимы различные статистические закономерности, полученные для всего изучаемого процесса в целом, а не только по отдельным его измеренным частям, фрагментам или показателям. Поэтому комплексные многофакторные измерения предпочтительнее однофакторных и частных исследований.

Поэтому все девять пробных площадок на разных глубинах взятия проб почвы мы принимаем за один комплекс, по которым можно выявить инвариантные от местности закономерности факторных связей.

По данным [4] была составлен список факторов (табл. 1). По закону Барии Коммонера принимается, что факторы взаимно зависимые.

Таблица 1

Табличная модель физико-химические свойств почвы с пробных площадок

№ п/п	pH↑	pHг↑	OH↑	K2O ↓, мг/100г	P2O5 ↓, мг/100г	Ca + Mg↓, мг/экв.100г	гумус↓, %
1	6.92	5.69	90.80	15.13	3.25	56.00	7.05
2	7.21	4.49	91.40	11.75	6.75	48.00	6.24
3	7.47	1.49	96.20	20.75	11.50	38.00	4.04
4	7.42	11.27	72.70	14.00	23.75	30.00	0.39
5	7.65	1.89	94.40	23.00	23.00	32.00	0.19
...	...	...	...	...	...	...	...
44	7.12	1.58	93.41	20.60	35.60	22.40	не опред.
45	6.09	6.39	83.00	20.60	17.80	31.20	6.85
46	6.50	4.9	85.30	14.00	17.80	28.40	3.31
47	6.84	2.45	92.26	17.20	19.60	29.20	0.78
48	6.93	2.01	93.80	17.20	28.60	30.40	0.74
49	6.92	2.45	90.70	22.00	30.30	24.00	не опред.

В таблице 1 приняты следующие условные обозначения: pH - кислотность водная; pH_г - кислотность гидролитическая; OH - степень насыщенности почвы основаниями, %;  - вектор ухудшения показателя «лучше →хуже». Примем вектор направления «лучше →хуже» для почвы по показателям pH и pH_г от щелочности к кислотности. Тогда возрастание кислотности хуже для почвы. Снижение концентрации химических соединений и гумуса также хуже для почвы.

Принцип суперпозиции данных экспериментов широко применяется в геоботанике [2]. Он называется принципом дополнительности.

По принципу дополнительности Гейзенберга и Бора, первоначально сформулированные в классической физике, отдельные частные статистические исследования, проведенные в разное время, на различных территориях и многими авторами, можно рассматривать совместно, так как статистические закономерности обладают замечательным свойством проявляться везде одинаково. Это обстоятельство позволяет применять для доказательства тех или иных статистических закономерностей результаты, опубликованные в научной литературе, а также в учебниках и учебных пособиях, в разное время.

В данной статье относительно данных из [4, с.102-103, табл. 22], которые измерениями проб почвы проведены в одно время, на одной пробной площади и одними и теми же авторами, предполагается, что в полной мере исполняются следующие два методологических условия:

1)исходная информация достоверна, достаточно полна и адекватно отображает указанный авторами период исследования;

2)алгебраические уравнения являются решениями неизвестных дифференциальных уравнений и отражают сущность изучаемого явления, а значения параметров модели имеют содержательный смысл.

Второе условие снимается при использовании устойчивых законов распределения [3], уравнения которых достоверны и доказаны различными отраслями науки, а параметры имеют содержательный смысл.

Вот почему одна и та же формула, полученная по статистическим данным одного региона, может быть применена, после повторной идентификации на ПЭВМ для вычисления значений параметров модели (регрессионных коэффициентов уравнения), в другом регионе.

Для одной и той же территории, лучше всего в его естественных границах, например по бассейнам рек и их притоков, проведенные в разное время измерения вполне можно объединить в одну статистическую выборку. Причем каждое экологическое наблюдение становится зависимым как от прошлого экологического режима, так и от технологического поведения людей и свойств самих природных объектов.

Результат экологического измерения не будет независимым наблюдением, как это допускает классическая статистика массовых наблюдений. А объекты, в которых участвуют существа, изменяют процессы своего метаболизма и состояния места обитания.

Вот почему необходима новая методология статистического моделирования, которая изначально (априори) предполагает взаимозависимость и взаимовлияние всех учитываемых факторов, причем исходя из цикличности реакций экологической химии в почве и проявления волновых свойств любых биоэкологических процессов.

Ранговые распределения значений учтенных в экспериментах факторов необходимы для проверки добротности измерений и достаточной полноты табличной модели по количеству наблюдений. Ранг  - это последовательность целых числе 0, 1, 2, 3, ... . Он отличается от рейтингового места i = 1, 2, 3, ... наличием нуля. Поэтому ранг очень удобен из-за того, что в примерах будет конкретное значение показателя при нулевом ранге.

Ранжирование - процесс установления рангов. Этот процесс всегда желателен при векторе предпорядка предпочтительности типа «лучше хуже». Далее рассмотрим последовательно все семь показателей.

Кислотность водная pH. Трендом рангового распределения является экспоненциальный закон роста (рис. 1) по формуле

.                             (1)

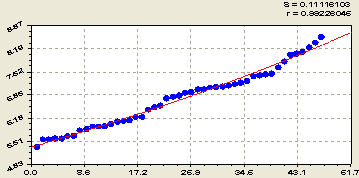
Рис. 1. Ранговое распределение водной кислотности

Коэффициент корреляции формулы (1) равен 0,9223.

Кислотность гидролитическая pH_г (рис. 2) изменяется так:

.     (2)

Распределение фактических значений в виде точек показывает наличие волновой составляющей к модели (2). Однако высокая адекватность формулы (2) с коэффициентом корреляции 0,9945 позволяет отказаться от волновых составляющих и в первом приближении применять только не волновые биотехнические закономерности.

Степень насыщенности почвы на разных глубинах основаниями OH (рис. 3) характеризуется уравнением вида

.                             (3)

Как видно из рангового распределения, радикалы в почве имеют большее колебание, чес кислотности двух видов.

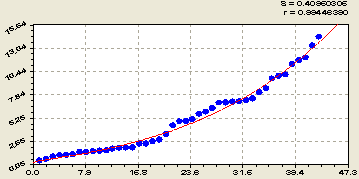
Рис. 2. Ранговое распределение гидролитической кислотности

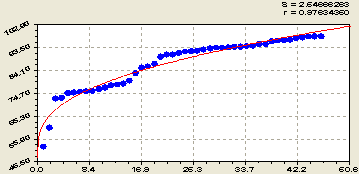
Рис. 3. Ранговое распределение насыщенности почвы основаниями

Подвижный калий K₂O, мг/100г. Это химическое соединение (рис. 4) определяется двухчленным уравнением вида

.           (4)

Здесь тренд содержит две составляющие, вторая из которых показывает кризис (отрицательный знак) в концентрации подвижного калия с 18-20 рангов. Как правило, вторая и последующие составляющие биотехнической закономерности показывают антропогенное влияние. Поэтому кризис калия в почве, начиная с некоторого уровня снижения её концентрации, возник из-за влияния человеческой деятельности.

Оксид фосфора P₂O₅, мг/100г. Он (рис. 5) изменяется по формуле

.                             (5)

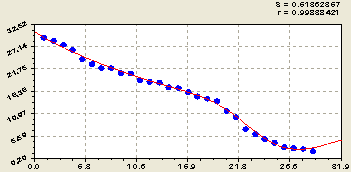
Рис. 4. Ранговое распределение в почве концентрации оксида калия

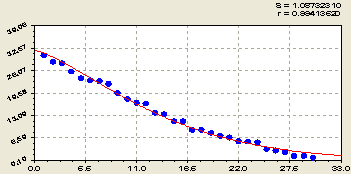
Рис. 5. Ранговое распределение в почве концентрации оксида фосфора

Закон гибели показывает естественную тенденцию изменения фосфора в почве изученного луга.

Сумма кальция и магния Ca+Mg дает (рис. 6) формулу вида

. (6)

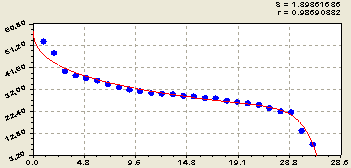
Рис. 6. Ранговое распределение в почве концентрации кальция и магния

Здесь кризис определяется по закону показательного роста и из ряда точек четко видно, что в конце ранжированного ряда концентрации суммы двух химических элементов резко снижается.

Содержание гумуса гумус, г. Это биологический показатель (рис. 7) определяется также законом экпсоненциальной1 гибели

.            (7)

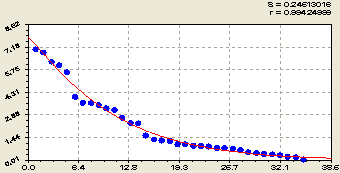
Рис. 7. Ранговое распределение в почве содержания гумуса

Таким образом, по ранговым распределениям из семи параметров почвы тревогу вызывают Ca+Mg и K₂O.

Литература

1. Захаров, К.К. Основы почвоведения и географии почв: Учебное пособие / К.К. Захаров.. - Йошкар Ола: МарГТУ, 1999. - 342 с.
2. Кучеров, И.Б. О принципе дополнительности в геоботанике. Методологические предпосылки возникновения комплементарных подходов к изучению растительности / И.Б. Кучеров // Журнал общей биологии. - 1995. - Том 56,
   № 4. - С.486-505.
3. Мазуркин, П.М. Геоэкология: Закономерности современного естествознания / П.М. Мазуркин. - Йошкар-Ола: МарГТУ, 2006. - 336 с.
4. Экология города Йошкар-Олы: научное издание / Мар.гос.ун-т; отв.ред. О.Л. Воскресенская. - Йошкар Ола, 2007. - 300 с.