Научная электронная библиотека

Монографии, изданные в издательстве Российской Академии Естествознания

Охрана и защита, обустройство, индикация и тести-рование природной среды. Сборник статей студентов, аспирантов и преподавателей: Научно-учебное издание

Мазуркин П. М.,

АНАЛИЗ ФИЗИКО-ХИМИЧЕСКИХ ПАРАМЕТРОВ ПОЧВЫ (П.М. Мазуркин, С.П. Семенова, магистрант (ЗОС-51))

Рассмотрим 11 уравнений факторных связей при коэффициенте корреляции не менее 0,5. Общая двухчленная формула имеет вид

,                (1)

где y - зависимый фактор (показатель), x - влияющий фактор, y₀ - начальное значение зависимого показателя от нулевого значения влияющего фактора,  - параметры статистической модели (1).

В таблице 1 приведены параметры модели (1). В итоге образуется компактная запись статистических моделей.

Первая составляющая формулы (1) является естественной закономерностью и, как правило, показывает природное снижение активности одного химического вещества при увеличении концентрации другого химического элемента или соединения различных элементов. Вторая составляющая характеризует стрессовое возбуждение зависимого фактора (химического вещества) от нарастающего содержания в почве влияющего фактора (химического вещества).

Если знак перед вторым членом уравнения (1) станет отрицательным, то это покажет кризисный характер изменения зависимого фактора от влияющего фактора. Положительный знак внутри экспоненты у первой составляющей модели (1) покажет стимулирующее влияние переменной x на показатель y.

Таблица 1

Параметры модели (1) бинарных связей выше среднего между свойствами почвы

Рей- тинг	Факторы		Параметры статистической модели (1)							Коэф. корр.
	x	y	y0	a1	a2	a3	a4	a5	a6
1	OH	pHг	4.70238	-0.017510	1	-1.04643e-26	16.86194	0.14553	1	0,9471
2	pHг	OH	99.44220	0.026641	1.08352	0	0	0	0	0,8990
3	pH	pHг	6,53617е7	9,23242	0,30998	0	0	0	0	0,8229
4	OH	pH	5.30718	-0.00067483	1	3.23642e-15	7.44067	0	0	0,8196
5	pH	OH	0	0	0	1,78918е7	13.15967	19.81048	0.33185	0,8063
6	pHг	OH	8.46446	0.11247	0.52406	0	0	0	0	0,7970
7	Ca+Mg	OH	43.75356	-0.011876	1.02509	1.91127e-6	6.75502	0.18422	1.05275	0,687
8	pHг	гумус	0	0	0	2.11642e8	14.30098	22.65144	0.36097	0,649
9	OH	Ca+Mg	0	0	0	1.05610e-9	7.07199	0.14776	0.87723	0,573
10	P2O5	pH	6.09844	-0.0059393	1	7030.3631	15.00229	19.84675	0.34266	0,536
11	pH	P2O5	0	0	0	1.77480e-15	37.63466	5.70059	0.95400	0,504

На рисунках 1-5 показаны графики по уравнениям из таблицы 1. При этом образовались три триады влияния степени насыщенности почвы основаниями OH, гидролитической кислотности pH_г и водной кислотности pH луговой почвы. Обособленно выглядят влияния Ca+Mg и оксида фосфора P₂O₅.

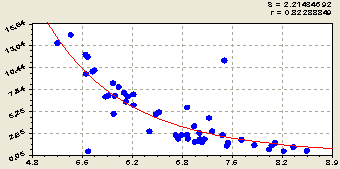
Из графиков на рисунке 1 видно, что гидролитическая кислотность приобретает максимальное значение от степени насыщенности почвы основаниями в интервале 55-65 %. С дальнейшим ростом переменной гидроксильной группы показатель pH_г  резко снижается.

Водная кислотность растет по экспоненциальному закону, а концентрация суммы кальция и магния достигает максимума при 93-95 %.

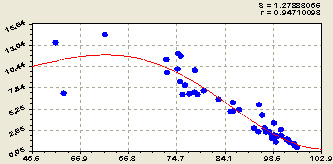
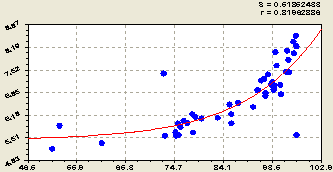
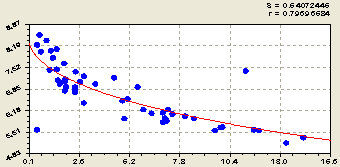
На рисунке 2 приведены графики влияния гидролитической кислотности pH_г на другие параметры почвы.

Из графиков и параметров модели (1) из таблицы 1 видно, что с ростом гидролитической кислотности луговой почвы степень насыщенности её основаниям и водная кислотность уменьшаются по закону экспоненциальной гибели, а оптимальное содержании гумуса (статистически в среднем) находится в интервале гидролитической кислотности 4,5-5,0.

Влияние гидроксильной группы на гидролитическую кислотность,

Влияние оснований в почве на водную кислотность,

Влияние гидроксильной группы на концентрацию кальция и магния,

Рис. 1. Изменение химических веществ от степени насыщенности почвы основаниями

Влияние гидролитической кислотности на основания в почве,

Влияние гидролитической кислотности на водную кислотность,

Влияние гидролитической кислотности на содержание гумуса в почве,

Рис. 2. Изменения химических веществ от роста гидролитической кислотности почвы

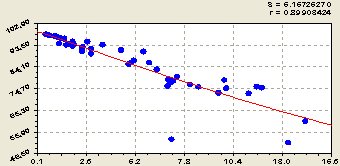
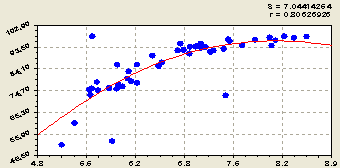
На рисунке 3 приведены графики влияния водной кислотности pH луговой почвы на три химических соединения.

Влияние водной кислотности на гидролитическую кислотность,

Влияние водной кислотности на основания в почве,

Влияние водной кислотности на концентрацию фосфора в почве,

Рис. 3. Изменения химических веществ от роста водной кислотности почвы

Здесь максимум появился у показателя OH около 95 % в интервале водной кислотности 9,0-9,3. А также четко проявился среднестатистический максимум 17-18 мг/100г содержания оксида фосфора в интервале водной кислотности 7,5-8,0. Таким образом, взаимные связи между химическими веществами почвы не только сложные (явно не линейные), но еще имеют множество максимумов и минимумов. Поэтому для каждого конкретного земельного участка с почвой будут и разные бинарные соотношения между химическими соединениями.

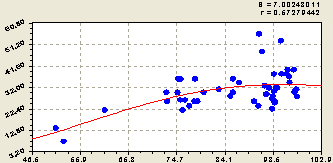
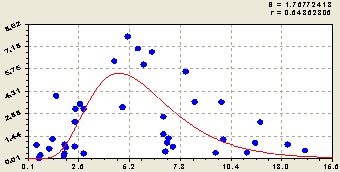
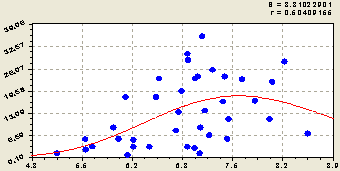
На рисунке 4 приведен график влияния суммы кальция и магния на степень насыщенности почвы основаниями.

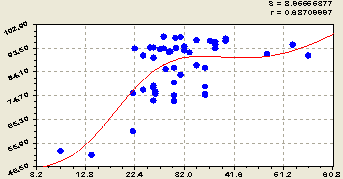
Рис. 4. Влияние суммы кальция и магния на основания в почве

Здесь и на последующем рисунке четко заметны два процесса, происходящих на пробной площади с девятью пробными площадками с различной растительностью: во-первых, экспоненциальный рост влияния переменой; во-вторых, стрессовое возбуждение значений показателя в некотором интервале изменения влияющей переменной. При сложении двух процессов возникает максимум, который на рисунке 4 есть среднестатистическое значение в основной группе наблюдений.

На рисунке 5 показан график влияния концентрации оксида фосфора на водную кислотность почвы.

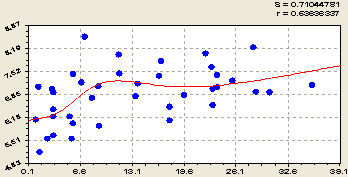
Рис. 5. Влияние фосфора в почве на водную кислотность

Оксид фосфора с возрастанием в интервале 3-23 мг/100г приводит водную кислотность почвы к стрессовому возбуждению.

По готовым статистическим моделям с параметрами из данных таблицы 1 вполне можно рассчитать активность взаимного влияния химических веществ почвы с разной растительностью, а также их коэффициенты приспособляемости к окружающей растительной среде.