Научная электронная библиотека

Монографии, изданные в издательстве Российской Академии Естествознания

Охрана и защита, обустройство, индикация и тести-рование природной среды. Сборник статей студентов, аспирантов и преподавателей: Научно-учебное издание

Мазуркин П. М.,

ФРАКТАЛЬНЫЙ АНАЛИЗ СТРУКТУРЫ МАЛОЙ РЕКИ (П.М. Мазуркин, А.А. Иванов, Н.Ю. Кораблева, бакалавриат (ПО-31))

В статье даны структурные особенности строения речной системы реки Лаж. Публикации, например в [1], свидетельствуют об актуальности изучения распределений элементов речной сети в виде групп притоков. Исходные данные для фрактального анализа приняты из книги «Справочник по длинам рек Поволжья». Речная система реки Лаж содержит 89 измеренных притоков.

По данным [1], важным объектом геоинформационного моделирования, как класса моделирования пространственно-временных данных, являются речные сети. В настоящее время адекватная параметризация речной сети в значительной степени обусловлена потребностью в развитии базовых представлений о пространственной структуре речных сетей. Применение степенных законов, связывающих основные геоморфологические характеристики речных систем, к описанию строения речных бассейнов, за последние 50 лет было подробно изучено в рамках теории речных сетей Хортона‑Страллера. Однако в середине 80-х годов XX века сформировался новый подход к анализу структуры речных сетей, объединяющий степенные законы и самоподобие в контексте теории фракталов. Этот подход обусловлен логикой развития современной естественнонаучной парадигмы. Действительно, речные сети представляют собой открытые сильно неравновесные системы, строение и эволюция которых определяются приходящим из окружающей среды потоком воды.

Актуальность темы связана с поиском единого подхода к моделированию речных сетей фрактальными методами, который позволил бы широко использовать самоподобную природу речных сетей при решении задач геоинформатики, гидрологии, геоморфологии, картографии и др. наук. Существующие фрактальные модели не заложены практически ни в одну из существующих геомоделей.

При этом нам известно, что в мировой науке фракталы пока не удалось формализовать математическими моделями.

Однако фракталы являются великолепными измерителями иерархических структур и дают принципиально новую размерность. Поэтому целью статьи является применение фрактальной размерности речной сети по кластерам, но, отказавшись от классификации Хортона и введя новую шакалу иерархии - ранг притока, когда за нулевой ранг принимается сама река, то есть главный водоток, и статистическое моделирование фрактальных распределений.

Известен способ измерения речной сети порядками водотоков [2, с.47-48], включающий классификацию измеренных притоков реки по Р. Хортону по различным порядкам водотоков, начиная от самых малых неразветвленных притоков. Затем вычисляются суммы длин водотоков данного порядка, средние длины притоков каждого порядка делением суммы длин на количество водотоков данного порядка, вычисление отношения средней длины притоков данного порядка к средней длине притоков следующего более низкого порядка, учет коэффициента бифуркации числа притоков.

Недостатком способа является то, что не учитываются в расчетах распределение притоков речной сети по порядкам водотоков, а расчеты по средним арифметическим длинам притоков не дают достаточной для практической гидрологии и ландшафтного обустройства территории точности вычислений гидрологических и иных показателей.

Известен также способ измерения речной сети порядками водотоков [3, с. .33-43], включающий распределение измеренных водотоков речной сети по порядкам Хортона-Штралера, классификацию водотоков по порядкам, площади водосбора, длине главной реки и среднему многолетнему расходу в устье главной реки (там же, с.33, табл. 2.1).

Недостатком является то, что распределение водотоков речной сети выполнено только по эвристической географической закономерности в виде табличной модели. При этом по измеренным водотокам не выявлены статистические закономерности по устойчивым математическим законам распределения. Таким образом, классическая нисходящая схема Хортона-Штралера, обладающая простотой и отсутствием субъективизма в определении порядка, применена к классификации структуры речной сети только с учетом измеренного множества притоков и без учета еще неизмеренных порядков водотоков.

Нами нулевой фрактальный ранг присваивается последнему порядку Хортона-Штралера, а последний ранг присваивается первому порядку Хортона-Штралера, причем последующие по возрастанию ранги присваиваются неизмеренным водотокам, мелким по сравнению с измеренными на карте данного масштаба водотоками.

Сущность нашего технического решения заключается в том, что принимается естественный порядок восходящего разветвления речной сети. Это позволяет учесть в конкретной статистической закономерности, идентифицируемой по устойчивому закону, как измеренные популяции водотоков, так и не измеренные (чаще всего из масштаба применяемых карт, например карты масштаба 1:500000 не позволяют учитывать водотоки длиной менее 5 км) популяции мелких по сравнению с первым порядком Хортона-Штралера водотоков. Применение простого устойчивого закона позволяет легко прогнозировать ориентировочную численность популяций мелких неизмеренных водотоков и тем самым оценивать экологическую устойчивость речной сети и вычислять риск от потери мелких притоков из-за хозяйственной деятельности, климатических изменений и других факторов внешней среды.

Затем, после проведения дополнительных измерений (например, с использованием снимков космической или вертолетной съемки), появляется возможность проверки расчетной численности неизмеренных популяций водотоков.

Положительный эффект достигается тем, что появляется практическая возможность многократной корректировки результатов измерений на картах. Известно, что при составлении карт, по которым проводятся измерения параметров речной сети (в данном случае числа водотоков малых порядков), выполняется цензовый отбор линейных элементов (например. рек, длина которых на карте меньше 1 см). Это цензовое требование [4, с. .142-143, 136] заставляет составителей карт исключать те водотоки, которые меньше по длине масштаба создаваемой карты. Ценз отбора по линейным элементам искусственно вводит ограничение на порядок водотоков по Р. Хортону, но никак не сказывается на ранг притоков по нашему способу измерений и моделирования речной сети.

В таблице 1 приведена характеристика 90 водотоков реки Лаж.

Таблица 1

Структура речной сети реки Лаж

Наименование водотока (притока)	Ранг r	Длина L, км	Наименование водотока (притока)	Ранг r	Длина L, км
Река Лаж	0	85.2	8 пр. пр. из Кочанур	2	1
1 пр. пр.	1	0.8	14 пр.пр. из Селюнино	1	11.7
2 пр. пр. из Ст. Юледур	1	1.3	1 л. пр. 14-го пр. из Мал. Гари	2	3.2
3 л. Пр.	1	1.6	2 л. пр. 14-го пр. в Мари-Пижай	2	1.7
4 л. Пр. из Иги-Сола	1	3.1	15 пр	1	8.6
5 пр. пр. из Ляждур Рус	1	1.5	16 л. пр. выше Бор	1	1.7
6 пр.пр. из Кушнур	1	4.8	17 пр.	1	10.2
1 пр. 6-го пр. в Умерке	2	0.6	18 пр. пр.	1	1.7
7 пр. пр. из Кырмыж	1	1.3	19 пр. пр. из Тетерино	1	3.3
8 пр.пр. р. Сеснур	1	7	20 пр.	1	8.2
1 пр. пр. 8-го пр. в Шой-Олма	2	0.8	1 пр. пр. 20-го пр.	2	0.1
2 пр. пр. 8-го пр. из Ниж. Сеснур	2	1	2 пр. пр. 20-го пр.	2	0.2
9 л.пр. р. Нолька	1	15.8	21 л.пр. р. Она	1	26.2
1 л.пр. 9-го пр. из Нур-Сола	2	4.2	1 пр.пр. 21-го	2	2.2
1 л. 1-го пр. в Ниж. Речеж	3	1.8	1 л. пр. 1-го пр.	3	0.6
2 л. пр. 9-го пр.	2	1.2	2 л. пр. 21-го пр.	2	3.4
3 пр.пр. 9-го пр.	2	2.1	3 пр.пр. 21-го пр.	2	3.6
1 пр. 3-го пр.	3	0.1	1 пр. пр. 3-го пр.	3	0.8
10 пр. пр. из Тамшинер	1	3.1	4 пр. пр. 21-го пр. из Обда-Сола	2	1.3
1 л. пр. 10-го пр.	2	0.7	5 л.пр. 21-го пр.	2	10.4
11 л.пр. из Огай	1	15	1 пр. пр. 5-го пр. в Шаба, прсх.	3	1.8
1 л. пр. 11-го пр. из Чендемерово	2	2.3	2 пр. пр. 5-го пр. из Кугунур, прсх.	3	3.9
2 л. пр. 11-го пр.	2	0.4	6 л.пр. 21-го пр.	2	12.3
3 пр. пр. 11-го пр.	2	4.7	1 л. пр. 6-го пр.	3	1.4
1 л. пр. 3-го пр. из Верх. Кученер	3	1	7 пр. пр. 21-го пр. из Кожланур	2	2
12 пр. пр. р. Ляж	1	1.7	22 пр.пр. р. Лаж	1	3.2
13 л. пр. р. Сердяжка	1	21.8	1 л. пр. 22-го пр.	2	0.3
1 л. пр.	2	0.9	23 л. пр.	1	2.8
2 л. пр. из Шоркинер	2	3.9	1 л. пр. 23-го пр., прсх	2	0.5
3 л.пр. из Токтарово	2	2.4	24 л. пр. из Осиновый Ключ, прсх	1	2
1 пр. 3-го пр.	3	0.4	25 л.пр. р. Пузя	1	13.4
5 пр. из Куприяново	2	7.4	1 л. пр. 25-го пр., прсх.	2	0.3
6 пр. пр. из Сернур	2	1.3	2 пр. пр. 25-го пр., прсх.	2	1.5
7 пр. пр.	2	0.7	3 пр. пр. 25-го пр. из Герас., прсх.	2	1.2
26 л.пр. р. Лаж	1	4.5	5 пр. пр. 27-го пр., прсх.	2	0.7
1 пр. пр. 26-го пр.,прсх.	2	0.1	28 пр.пр. р. Лаж	1	12.3
27 л. пр. р. Чукша	1	20.2	1 пр. пр. 28-го пр., прсх.	2	0.6
1 л. пр. 27-го пр., прсх.	2	1	29 л. пр. из Кошкино, прсх.	1	4.4
2 л.пр. 27-го	2	2.2	30 пр. пр. из Б. Торма, прсх.	1	2.5
1 пр.2-го пр.	3	0.8	31 л.пр. из Шахурдино	1	7.4
3 л.пр. 27-го пр.	2	1.7	1 пр.пр. 31-го пр.	2	2.5
4 л. пр. 27-го пр.	2	1.7	1 пр. пр. 1-го пр., прсх.	3	0.1
1 л. пр. 3-го пр., прсх.	3	0.3	32 пр.пр. р. Лаж	1	6.6
1 л. пр. 4-го пр.	3	0.3	1 л. пр. 32-го пр. из Песемерь	2	1.5
2 пр. пр. 4-го пр.	3	0.2	33 пр. пр.	1	0.8

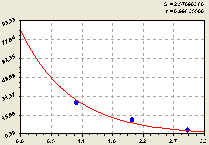
После идентификации биотехнического закона была получена (рис. 1) устойчивая биотехническая закономерность вида

.                               (1)

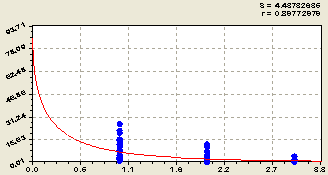
Рис. 1. График фрактального распределения длины притоков речной сети Лаж

Не нарушенная хозяйственной деятельностью населения или природной катастрофой речная сеть обладает замечательным фрактальным свойством, когда в ранговом распределении длина самой реки становится начальным значением в устойчивом законе экспоненциальной гибели типа формулы (1).

Чем больше коэффициент корреляции (в правом верхнем углу рисунка 1), тем экологически устойчивее речная сеть, то есть на её территории меньше нарушений территориального компонентного экологического равновесия (баланса).

Коэффициент корреляции 0,8977 показывает сильную факторную связь. Расстроенная речная сеть будет иметь меньшую корреляцию в длинах притоков по уровням фрактала (рангам притоков).

Каждый из трех уровней фрактальности притоков получает собственные ранговые распределения. Это и доказывает фрактальную размерность речной сети. Пространственный            график распределения фактических данных измерений длины притоков приведен на рисунке 2.

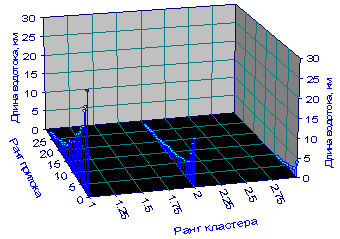
Рис. 2. Поверхность фрактального распределения длины притоков реки Лаж

Здесь появился новый объясняющий параметр  - ранг длины притока, распределяемый по убыванию длины водотока.

По-видимому, математически возможно получение двухфакторной биотехнической закономерности типа . Но для этого нужна специальная программная среда, которая была бы эффективней среды TableCurve 3D, поэтому в дальнейшем были получены однофакторные зависимости типа  и  в среде CurveExpert-1.38.

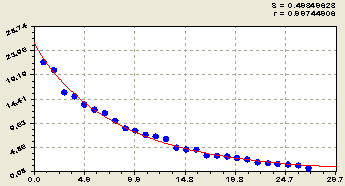
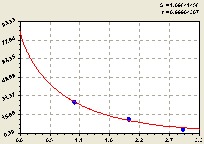
Рис. 3. График распределения длины притоков первого фрактала речной сети Лаж

Если из данных таблицы 1 выделить строки при ранге кластера (фрактальной размерности) r =1, то внутри этой группы притоков получили (рис. 3) закономерность распределения в виде формулы

.                           (2)

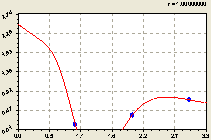
На втором фрактальном уровне (рис. 4) получили формулу

.                           (3)

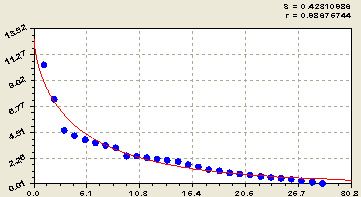
Рис. 4. График распределения длины притоков второго фрактала речной сети Лаж

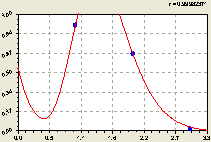
На третьем уровне фрактальности получена (рис. 5) зависимость

.                           (4)

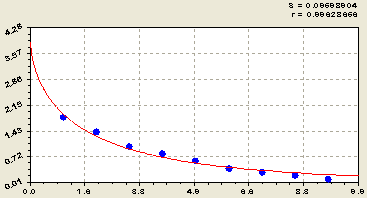
Рис. 5. График распределения длины притоков третьего фрактала речной сети Лаж

Косвенно выяснили, что математической моделью любой фрактальной размерности некой иерархической структуры является экспоненциальный закон гибели, предложенный проф. П.М. Мазуркиным, и, в отличие от закона Лапласа в так называемых лапласианах (закона Ципфа в биологии, Парето в экономике и Мандельброта в физике), имеющего параметр интенсивности ≠1.

Изменение закона гибели от формы  к конструкции  позволяет моделировать любые фракталы, в том числе в виде множества из асимметричных вейвлет-сигналов [5].

Если речная сеть действительно подчиняется фрактальной размерности, то все полученные закономерности сами должны подчиняться по значениям параметров общей модели экспоненциальной гибели.

Для доказательства все данные приведены в таблице 2.

Таблица 2

Речная сети реки Лаж и параметры фрактальных закономерностей

Ранг фрактала	Длина , км	Параметры экспоненциального закона гибели
		L0, км	Активность a1	Интенсивность a2
0	85.2	85.20095	2.50187	0.54653
1	26.2	25.70279	0.14476	0.91419
2	12.3	12.64762	0.35998	0.66645
3	3.9	3.87957	0.71778	0.02673

Сравнение параметров и показывает малую погрешность между ними и высокую адекватность моделирования фракталов законом экспоненциальной гибели. Максимальные длины притоков в каждом кластере (в нулевом кластере всего один водоток, но их может быть больше на крупных реках) характеризуются уравнениями (рис. 6):

- по закону Мандельброта

;                              (5)

- по закону проф. П.М. Мазуркина

.                          (6)

По закону Манбельброта	По закону П.М. Мазуркина

Рис. 6. Графики рангового распределения длины наибольшего водотока

Река Лаж и её притоки пока имеют высокое экологическое качество и мало нарушены человеком. Поэтому более простой закон Мандельброта, с интенсивностью спада a₂=1, получает высокое значение коэффициента корреляции 0,9984. Но биотехнический закон, частным случаем которого является закон экспоненциальной гибели (6), дает коэффициент корреляции 0,9996.

Разница 0,9996 - 0,9984 = 0,0012 в коэффициентах корреляции двух формул вроде бы очень малая, однако с ростом количества и интенсивности нарушений экологического равновесия, на территории водосборного бассейна речной сети эта разница существенно увеличивается. Поэтому закон Лапласа-Мандельброта становится неадекватным реальной действительности относительно нарушенной хозяйственной деятельности людского населения именно из-за упрощения a₂=1.

По закону гибели в полной конструкции параметры активности  и интенсивности  спада значений изучаемого показателя сами изменяются, в зависимости от ранга фрактальной размерности, по формулам биотехнических закономерностей (рис. 7):

;  (7)

.       (8)

Для крупных рек с количеством притоков 500 и более, число кластеров возрастает, поэтому полная конструкция формул (7) и (8) будет

,                (9)

где b₁, ....b₇ - параметры общей статистической модели (9).

Из графиков на рисунке 7 видно, что формулы (7) и (8) симметричны относительно фрактальной размерности.

Активность экспоненты	Интенсивность  экспоненты

Рис. 7. Графики рангового распределения параметров закона П.М. Мазуркина

Таким образом, естественный предпорядок предпочтительности, определяемый фрактальной структурой речной сети по двум рангам каждого притока (фрактального по примыканию и убывающего по длине), обеспечивает получение устойчивых закономерностей распределения водотоков по их длине.

Литература

1. Учаев, Д.В. Методика геоинформационного моделирования речных сетей на основе фрактальных методов / Д.В. Учаев // Автореф. .. к.т.н. - М.: МГУ геодезии и картографии, 2007. - 24 с.
2. Важнов, А.Н. Гидрология рек. Учебник для студентов спец. «География» / А.Н. Важнов. - М.: МГУ, 1976. - 339 с.
3. Географические закономерности гидрологических процессов юга Восточной Сибири / А.Н. Антипов, Н.В. Абасов, Т.В. Бережных и др. - Иркутск: Изд-во Института географии СО РАН, 2003. - 208 с.
4. Берлянт, А.М. Картография: учеб. / А.М. Берлянт. - М.: Аспект пресс, 2002.
5. Мазуркин, П.М. Статистическая модель периодической системы химических элементов Д.И. Менделеева / П.М. Мазуркин. - Йошкар-Ола: МарГТУ, 2006. - 152 с.