Научная электронная библиотека

Монографии, изданные в издательстве Российской Академии Естествознания

Охрана и защита, обустройство, индикация и тести-рование природной среды. Сборник статей студентов, аспирантов и преподавателей: Научно-учебное издание

Мазуркин П. М.,

ФАКТОРНЫЙ АНАЛИЗ ПОКАЗАТЕЛЕЙ ГЕОТРИАДЫ (П.М. Мазуркин, А.А. Иванов)

Применим первый закон экологии «всё связано со всем» [1, с.18] к подсистемам геотриады «территория - население - хозяйство» [2-7], причем рассматривая на первых порах только хозяйство людей [8, 9].

В таблице 1 приведены исходные данные для факторного анализа.

Примем вектор направления «лучше →хуже» для всех параметров подсистем и элементов геотриады. Тогда стрелка вверх указывает, что нарастание трех параметров речной сети будет лучше для экосистемы, а стрелка вниз показывает, что по населению и его хозяйству лучше всего снижать значения показателей.

По шести параметрам системы «территория - население - хозяйство» был выполнен факторный анализ двумя способами:

во-первых, с использованием только трендовых закономерностей;

во-вторых, с трендовыми и волновыми составляющими.

Таблица 1

Характеристика геотриады по бассейнам основных рек Республики Марий Эл

Речной бассейн	Территория			Население		Хозяйство
	Число рек ( км) I ↑, шт.	Длина рек сети L ↑, км	Площадь бассейна S ↑, км2	Плотность сельского населения  nc  ↓ , чел/км2	Жители в поселении , чел.	Кол-во поселений Z ↓, шт.
Сура	Нет данных	Нет данных	Нет данных	6.3	61	12
Сумка	8	77.7	199.1	35.5	104	64
Б. Юнга	8	91.0	176.0	38.2	132	50
М. Юнга	1	32.5	78.0	46.7	128	28
Б. Сундырь	4	80.0	196.0	49.7	139	77
Ветлуга	35	720.9	2257.5	1.9	172	39
Рутка	27	456.0	1833.9	13	216	25
Арда	5	131.0	352.0	7.3	270	11
Парат	2	70.0	545.1	1.3	119	3
Б. Кокшага	68	1008.0	6539.8	11	167	60
М. Кокшага	116	1571.1	5025.5	13.1	226	380
Илеть	97	1521.4	6571.4	11.2	218	291
Волга	Нет данных	Нет данных	Нет данных	7.1	258	34
Немда	54	725.0	3772.2	16.3	93	360
Буй	7	89.8	893.2	24.8	213	38
Уржумка	33	454.1	1790.2	14.1	198	75

 

Как известно, возмутителем экосистем чаще всего является людское население со своим хозяйством. Поэтому в геотриаде может оказаться, что трендовые модели будут иметь низкую корреляцию между факторами.

Для краткости в таблице 2 приведены только тренды, а в таблице 2 данные по трендам с одной волновой составляющей.

Как известно, грубая классификация уровней коэффициента корреляции следующая:

а) до 0,3 - нет связи между факторами;

б) от 0,3 до 0,7 - есть слабая связь между двумя факторами;

в) выше 0,7 - есть сильная связь между переменными факторами.

Из данных таблицы 3 видно, что нет факторной связи только по трем бинарным отношениям. Однако с волновыми составляющими эти же отношения сразу же переходят в разряд сильных связей.

Таким образом происходит раздвоение структуры модели на две части - не волновую и колебательную, показывающую возмущение того или иного параметра геотриады от влияния другого её фактора.

Тогда можем ввести новый показатель оценки гетриады - коэффициент бифуркации факторных связей как отношение коэффициентов корреляции в целом к этому же коэффициенту корреляции у тренда.

Таблица 2

Корреляционная матрица факторных связей между параметрами геотриады

Влияющие факторы (параметры) геотриады	Зависимые факторы (показатели) геотриады
	Число рек I, шт.	Длина рек сети L, км	Площадь бассейна S, км2	Плотность сельск. насел. nc, чел/км2	Жители в поселении , чел.	Кол-во поселений Z, шт.
Число рек I, шт.	0,9994 0,9948	0,9984 0,9905	1,0000 0,9953	0,9857 0,5717	0,9832 0,3867	0,9879 0,8228
Длина рек сети L, км	0,9958 0,9899	0,9988 0,9886	0,9966 0,9828	0,9539 0,6743	0,8878 0,3531	0,9947 0,7808
Площадь бассейна S, км2	0,9947 0,9521	0,9960 0,9376	1,0000 0,9945	1,0000 0,8450	0,9881 0,3470	0,9856 0,9206
Плотность сельск. насел. nc, ч./км2	0,8489 0,7798	0,9671 0,8122	0,9465 0,8834	0,9968 0,9859	0,9788 0,3053	0,8270 0,6054
Жители в поселении , чел.	0,8148 0,4773	0,8188 0,5140	0,7985 0,4523	0,9567 0,5752	0,9986 0,9926	0,7536 0,0552
Кол-во поселений Z, шт.	1,0000 0,8188	0,8740 0,7689	0,9702 0,6898	0,9943 0,0589	0,8541 0,0979	0,9988 0,9575

Примечание: в числителе приведены коэффициенты корреляции трендов и волновых составляющих, а в знаменателе - трендов статистической модели.

Таблица 3

Корреляционная матрица трендовых связей с коэффициентами корреляции ≥0,3

Влияющие факторы (параметры) геотриады	Зависимые факторы (показатели) геотриады
	I, шт.	L, км	S, км2	nc, чел/км2	, чел.	Z, шт.
Число рек I, шт.	0,9948	0,9905	0,9953	0,5717	0,3867	0,8228
Длина рек сети L, км	0,9899	0,9886	0,9828	0,6743	0,3531	0,7808
Площадь бассейна S, км2	0,9521	0,9376	0,9945	0,8450	0,3470	0,9206
Плотность сельск. насел. nc, ч./км2	0,7798	0,8122	0,8834	0,9859	0,3053	0,6054
Жители в поселении , чел.	0,4773	0,5140	0,4523	0,5752	0,9926
Кол-во поселений Z, шт.	0,8188	0,7689	0,6898			0,9575

Бифуркация (лат.bifurcatio) - раздвоение, разделение, разветвление чего-л., напр. Разделение реки (и её долины) на два протока, из которых один вливается в реку другой системы; в анатомии - разделение трубчатого органа на две ветви, напр. трахеи на два бронха [10, с.110].

Из этого определения следует, что бифуркация геотриады - это её разделение на естественное (тренды) и колебательное (волновые составляющие). Здесь можно привести также и физическую аналогию: в гидрологии ламинарное (тренд) и турбулентное (колебание) течения возникают последовательно, а в таблице 2 - параллельно.

Поделив в таблице 2 числитель на знаменатель, получим матрицу коэффициентов бифуркации факторных связей геотриады (табл. 4).

Таблица 4

Коэффициенты бифуркации факторных связей геотриады

Влияющие факторы (параметры) Геотриады	Зависимые факторы (показатели) геотриады
	I, шт.	L, км	S, км2	nc, чел/км2	, чел.	Z, шт.
Число рек I, шт.	1,0046	1,0080	1,0047	1,7242	2,5425	1,2007
Длина рек сети L, км	1,0060	1,0103	1,0140	1,4147	2,5143	1,2739
Площадь бассейна S, км2	1,0447	1,0623	1,0055	1,1834	2,8476	1,0706
Плотность сельск. насел. nc, ч./км2	1,0886	1,1907	1,0714	1,0111	3,2060	1,3660
Жители в поселении , чел.	1,7071	1,5930	1,7654	1,6632	1,0060	13,6522
Кол-во поселений Z, шт.	1,2213	1,1367	1,4065	16,8812	8,7242	1,0431

Ранговые распределения значений факторов (клетки по диагонали таблицы 3) имеют небольшие волновые возмущения, при этом по трендам (см. табл. 3) все шесть монарных отношений имеют коэффициент корреляции выше 0,95. Наибольше возмущение по значениям имеет фактор «Количество поселений Z, шт.».

Наибольший коэффициент бифуркации 16,8812 получило влияние параметра геотриады «Количество поселений Z, шт.» на показатель «Плотность сельского населения n_c, чел./км²». Тогда по данным таблицы 1 хозяйство влияет на население чрезвычайно сильно с колебаниями (флюктуациями в поведении).

С коэффициентом бифуркации 13,6522 влияет переменная «Жители в среднем в поселении , чел.» на зависимый фактор «Количество поселений Z, шт.». На третьем рейтинговом месте, с коэффициентом бифуркации 8,7242, находится бинарное отношение «Количество поселений Z, шт.»  «Жители в среднем в поселении , чел.». С коэффициентом бифуркации 3,2060 на четвертом месте находится пара «Плотность сельского населения n_c, чел./км²» → «Жители в среднем в поселении , чел.».

В итоге можно выделить две части (табл. 5) геотриады.

В первой части находится территория речной сети, а во второй людское население со своим хозяйством. Как видно из данных таблицы 5, бифуркация сильна именно в поведении людей, а не в распределении параметров речной сети.

Причем из данных таблицы 6 видно, что всё же на водосборном бассейне РМЭ речные сети влияют на природно-антропогенные комплексы оказывают большее влияние, чем население со своим хозяйством на речные сети.

Таблица 5

Коэффициенты бифуркации факторных связей по двум частям геотриады

Влияющие факторы (параметры) Геотриады	Зависимые факторы (показатели) геотриады
	I, шт.	L, км	S, км2	nc, чел/км2	, чел.	Z, шт.
Число рек I, шт.	1,0046	1,0080	1,0047
Длина рек сети L, км	1,0060	1,0103	1,0140
Площадь бассейна S, км2	1,0447	1,0623	1,0055
Плотность сельск. насел. nc, ч./км2				1,0111	3,2060	1,3660
Жители в поселении , чел.				1,6632	1,0060	13,6522
Кол-во поселений Z, шт.				16,8812	8,7242	1,0431

Таблица 6

Коэффициенты бифуркации между двумя частями геотриады

Влияющие факторы (параметры) Геотриады	Зависимые факторы (показатели) геотриады
	I, шт.	L, км	S, км2	nc, чел/км2	, чел.	Z, шт.
Число рек I, шт.				1,7242	2,5425	1,2007
Длина рек сети L, км				1,4147	2,5143	1,2739
Площадь бассейна S, км2				1,1834	2,8476	1,0706
Плотность сельск. насел. nc, ч./км2	1,0886	1,1907	1,0714
Жители в поселении , чел.	1,7071	1,5930	1,7654
Кол-во поселений Z, шт.	1,2213	1,1367	1,4065

Наибольшее перекрестное бифуркационное влияние в двух частях геотриады оказывает площадь водосборного бассейна на среднюю численность жителей в одном сельском поселении, а наименьшее - средняя плотность сельского населения на площадь водосбора речной сети.

Обобщенная формула всех 36 факторных связей имеет вид:

,                   (1)

,  ,

, ,

, ,

, ,

где  - трендовая (ламинарная) часть модели,  - волновая (турбулентная) часть модели, y₁ - биотехнический закон или, что чаще всего, экспоненциальный закон (роста или гибели при условии a₂=0), y₂ - биотехнический закон, y₃, y₄ - волновые составляющие, A₁,  A₂- амплитуды (половины) колебательного возмущения, p₁, p₂ - периоды (половины) возмущающего влияния одного фактора на другой, a₁.....a₂₄ - параметры модели.

Коэффициент бифуркации k_б определится из выражения

,                  (2)

где R - коэффициент корреляции, показываемый CurveExpert-1.38.

Коэффициент динамичности факторной связи вычисляется так:

.                        (3)

В таблице 7 показаны структуры частных формул. При этом указаны последовательности номеров составляющих из уравнения (1).

Таблица 7

Структуры биотехнических закономерностей факторных связей геотриады

Влияющие факторы (параметры) Геотриады	Зависимые факторы (показатели) геотриады
	I, шт.	L, км	S, км2	nc, чел/км2	, чел.	Z, шт.
Число рек I, шт.	1,3	1,3	1,2,3	1,2,3	1,2,3	1,2,3
Длина рек сети L, км	1,3	1,3	1,2,3	1,2,3	1,3	1,3,4
Площадь бассейна S, км2	1,2,3	1,3	1,3,4	1,2,3	1,3,4	1,2,3
Плотность сельск. насел. nc, ч./км2	1,2,3	1,2,3	1,2,3	1,3	1,3,4	1,2,3
Жители в поселении , чел.	1,3	1,3	1,3	1,3	1,3	1,3
Кол-во поселений Z, шт.	1,3,4	1,3,4	1,3	1,3,4	1,3	1,3

При одной и той же адекватности чем меньше составляющих и параметров у этих составляющих, тем добротнее конструкция модели.

В таблице 7 находится 16 биотехнических закономерностей с кодами 1, 3 и имеющими по две составляющие.

Для выбора простейшей конструкции модели дана таблица 8.

Таблица 8

Количество параметров у закономерностей факторных связей геотриады

Влияющие факторы (параметры) Геотриады	Зависимые факторы (показатели) геотриады
	I, шт.	L, км	S, км2	nc, чел/км2	, чел.	Z, шт.
Число рек I, шт.	11	9	14	12	12	9
Длина рек сети L, км	8	10	15	12	10	12
Площадь бассейна S, км2	13	7	14	14	16	13
Плотность сельск. насел. nc, ч./км2	11	11	12	10	15	11
Жители в поселении , чел.	11	8	8	12	10	8
Кол-во поселений Z, шт.	17	12	12	18	10	9

Наипростейшее уравнение содержит семь параметров и имеет вид

, (4)

отличающееся от формулы Хортона-Штралера второй составляющей.

При этом без учета волнового возмущение (рис. 1) получили простой показательный закон в виде выражения

.              (5)

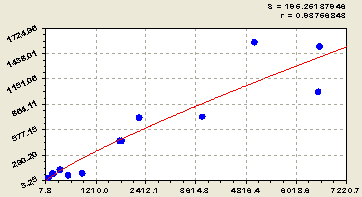
Рис. 1. График влияния площади водосбора речной сети на общую длину притоков

Геотриадное измерение речной сети вполне возможно, а фаткрный анализ параметров геотриады позволяет оценивать уровень антропогенной нагрузки на территорию водосборного бассейна речной сети.

Литература

1. Популярная экология (полезные советы в повседневной жизни): гл. ред. Н.П. Торсуев. - Казань: Экоцентр, 1997. - 236 с.
2. Мазуркин, П.М. Геотриадное измерение сельских территорий / П.М. Мазуркин, С.И. Михайлова // Межд. ж-л прикл. и фунд. исследований. - 2009. № 4. - С.28-35.
3. Мазуркин, П.М. Геоинформационные системы земельного кадастра, лесного реестра и особо охраняемых территорий / П.М. Мазуркин, А.Н. Фадеев // Современные проблемы науки и образования. - 2009. - № 4. - С.69-75.
4. Мазуркин, П.М. Иерархия сельхозпредприятий в сельском районе / П.М. Мазуркин // Современные наукоемкие технологии. - 2009. - № 7. - С.30-41.
5. Мазуркин, П.М. Анализ факторов произвдства сельского района / П.М. Мазуркин // Современные наукоемкие технологии. - 2009. - № 8. - С.55-62.
6. Мазуркин, П.М. Прошлое, современное состояние и перспективы лесоаграрной России / П.М. Мазуркин // Современные проблемы науки и образования. - 2009. - № 4. - С.93-112.
7. Мазуркин, П.М. Историографический анализ динамики населения России / П.М. Мазуркин // Межд. ж-л прикл. и фунд. иссл. - 2009. - №5. -С.56-69.
8. Мазуркин, П.М. Эконометрическое моделирование: практикум / П.М. Мазуркин, О.В. Порядина. - Йошкар-Ола: МарГТУ, 2009. - 204 с.
9. Мазуркин, П.М. К вопросу о методике оценки социально-экономического положения регионов / П.М. Мазуркин, О.В. Порядина // Междунар. ж-л прикл. и фундаментальных исследований. - 2009. - № 6. - С.11-17.
10. Словарь иностранных слов. - 5 изд., стер. - М.: Госиздат иностранных и национальных словарей, 1955. - 855 с.