Научная электронная библиотека

Монографии, изданные в издательстве Российской Академии Естествознания

Прикладные задачи динамики ледяного покрова

Козин В. М., Жесткая В. Д., Погорелова А. В., Чижиумов С. Д., Джабраилов М. Р., Морозов В. С., Кустов А. Н.,

4.5. Расчет прогибов ледяного покрова с ограниченным пространством свободной воды

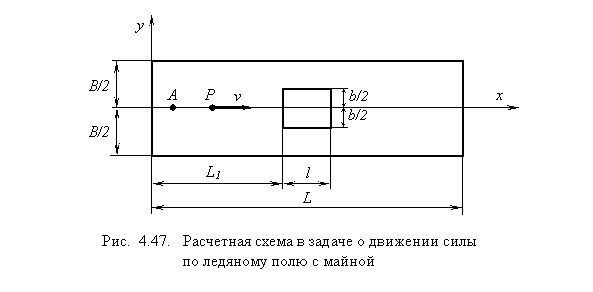
В реальных условиях может сложиться такая ситуация, когда на пути СВП, движущегося по ледяному полю, встречается ограниченное пространство чистой воды (полынья, майна). Представление об особенностях напряженно-деформированного состояния ледяного покрова, вызванных наличием майны и проявляющихся при нахождении судна вблизи от нее, можно составить, рассматривая следующую задачу: сосредоточенная сила Р движется с постоянной скоростью v по прямоугольной ледяной пластине с отверстием, жестко заделанной по контуру; траектория движения силы совпадает с осью симметрии пластины x ( рис. 4.47).

.

Представляет интерес исследование того, как влияют размеры майны на характеристики напряженно-деформированного состояния ледяного покрова, и, в частности, на его прогибы. Для решения этой задачи может быть использован метод, изложенный в [38] и [40]. Приведем расчет прогибов ледяного поля при следующих исходных данных: длина пластины L - 560 м, ширина В - 392 м; ширина майны - 112 м; L₁ - 224 м; толщина льда h = 0,5 м; глубина водоема H = 5 м; P = 0,4×10⁶ H; модуль Юнга для льда E = 0,73×10¹⁰ Па; коэффициент Пуассона n = 0,3; плотность льда r_i = 900 кг/м³; плотность воды r_w = 1000 кг/м³; время релаксации деформаций t_f = 10 с; скорость движения силы v равна резонансной скорости движения силы при данной глубине водоема и составляет 7 м/с. Рассматривались три значения длины майны l: 56, 112 и 168 м. При расчете было принято, что в начальный момент времени Р находится в точке А (28 м, 0) и имеет нулевую скорость, а пластина имеет соответствующий статический прогиб. Время t₀, за которое происходит разгон из состояния покоя до конечной скорости v, было принято равным нулю, так как длина пластины достаточна для того, чтобы к моменту прохождения майны процессы, протекающие при движении силы, приняли установившийся характер, на котором уже не сказываются особенности начального периода движения. Шаг сетки времени Dt был выбран равным 0,125 с.

Дискретизация пластины показана на рис. 4.48. При расчете учитывалась симметрия пластины и рассматривалась только ее часть при y £ 0. Дискретная модель состояла из квадратных конечных элементов со стороной a = 28 м. Майна длиной BC₁ = 56 м выделена на рисунке темным цветом. Правая граница майны длиной 112 и 168 м проходит через точки C₂ и C₃ соответственно.

.

Для каждого значения длины майны определялись прогибы пластины w в моменты времени, когда а) сила находилась на краю ледяного поля в точке B, то есть начинала проход через майну, и б) сила выходила на лед после прохода майны.

На рис. 4.49 – 4.58 представлены графики прогибов в точках пластины, расположенных на оси x в районе майны, для указанных моментов времени. Там же даны для сравнения графики прогибов, построенные для пластины без отверстия, при тех же значениях времени t. Ввиду малости прогибов в точках оси x, достаточно удаленных от точки приложения силы, соответствующие части графиков на рисунке не показаны. Положение силы Р обозначено стрелкой. Для наглядности в верхней части рисунков показано расположение майны.

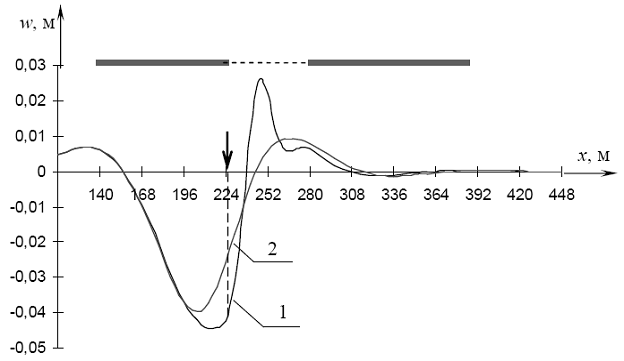
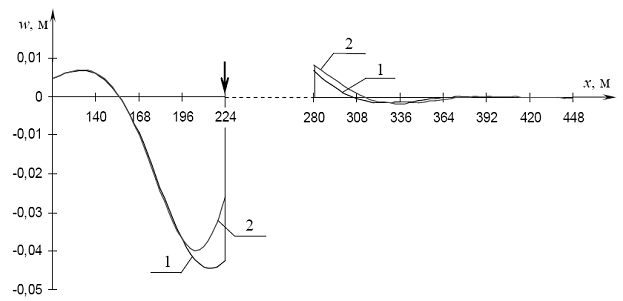
Графики на рис. 4.49 - 4.52 построены для случая, когда длина майны l равна 56 м. На рис. 4.49 представлен график прогибов ледяной пластины и перемещений свободной поверхности воды. На рис. 4.50 даны в увеличенном масштабе зоны предыдущего графика, содержащие только прогибы льда.

.

Рис. 4.49. Прогибы при проходе силы Р через точку B: 1 - при наличии майны (l = 56 м), 2 - для сплошного льда

.

Рис. 4.50. Прогибы льда при проходе силы Р через точку B: 1 - при наличии майны (l = 56 м), 2 - для сплошного льда

.

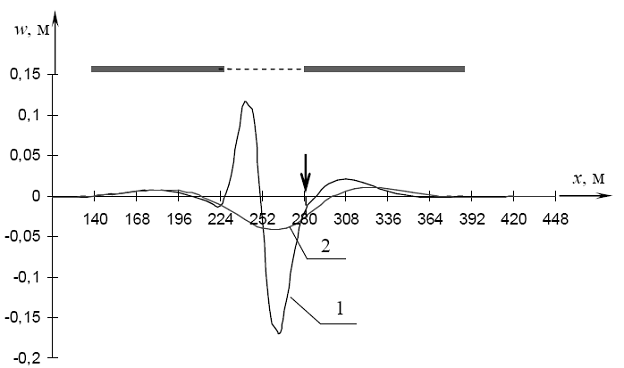
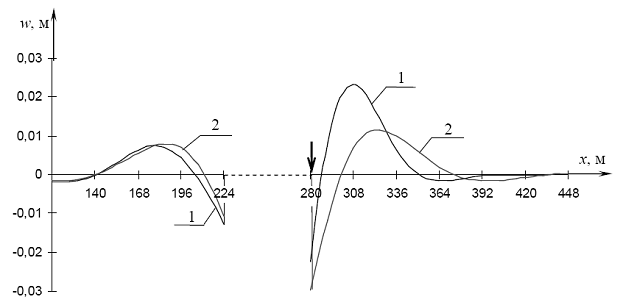
Рис. 4.51. Прогибы при проходе силы Р через точку C1: 1 - при наличии майны (l = 56 м), 2 - для сплошного льда

.

Рис. 4.52. Прогибы льда при проходе силы Р через точку C₁: 1 - при наличии майны (l = 56 м), 2 - для сплошного льда

Графики на рис. 4.53 - 4.55 отвечают случаю, когда длина майны l равна 112 м. На рис. 4.53 и 4.54 приведены графики прогибов ледяной пластины и перемещений свободной поверхности воды при сходе силы со льда на воду и при выходе силы на лед после прохода майны соответственно. На рис. 4.55 даны в увеличенном масштабе зоны предыдущего графика (см. рис. 4.54), содержащие только прогибы льда.

Графики, аналогичные предыдущим, приведены на рис. 4.56 – 4.58 для майны длиной 168 м.

.

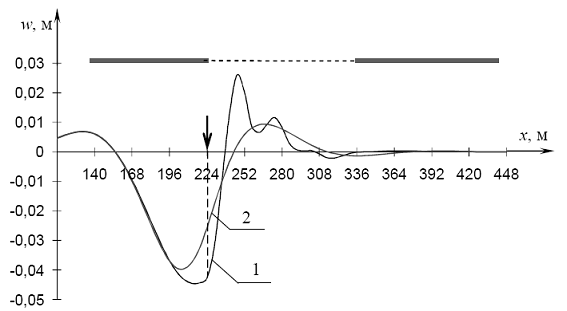
Рис. 4.53. Прогибы при проходе силы Р через точку B: 1 - при наличии майны (l = 112 м), 2 - для сплошного льда

.

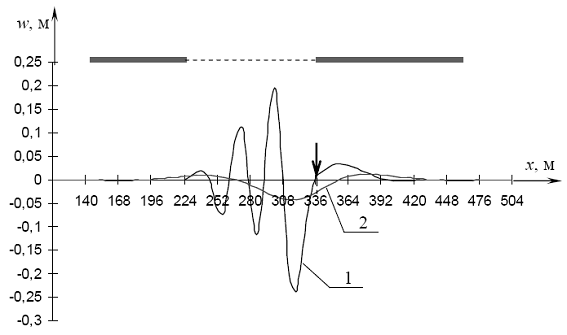
Рис. 4.54. Прогибы при проходе силы Р через точку C₂: 1 - при наличии майны (l = 112 м), 2 - для сплошного льда

.

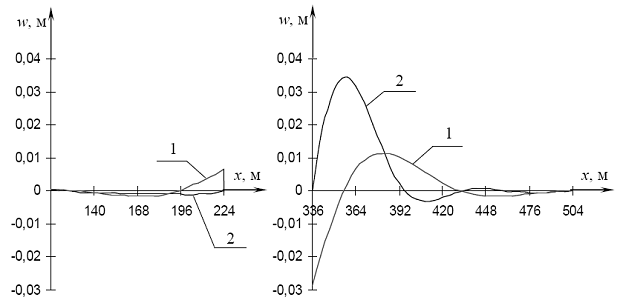
Рис. 4.55. Прогибы льда при проходе силы Р через точку C₂: 1 - при наличии майны (l = 112 м), 2 - для сплошного льда

.

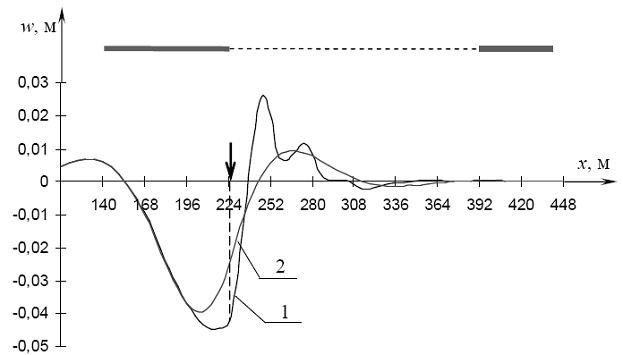
Рис. 4.56. Прогибы при проходе силы Р через точку B: 1 - при наличии майны (l = 168 м), 2 - для сплошного льда

Из приведенных выше графиков видно, что до того момента времени, когда сила входит в пределы майны, наличие последней почти не влияет на картину прогибов льда. Существенные отличия появляются после прохода майны: максимальное значение прогиба по сравнению со случаем пластины без отверстия заметно возрастает (предыдущие исследования показывают, что этот эффект ярче проявляется при меньшей скорости), причем тем больше, чем больше длина майны. Увеличение прогибов, по-видимому, объясняется тем, что при проходе нагрузки через майну в той образуется гравитационная волна гораздо большей амплитуды по сравнению с изгибно-гравитационной волной в сплошном ледяном поле, которая достигает края майны и усиливает воздействие силы Р на лед.

.

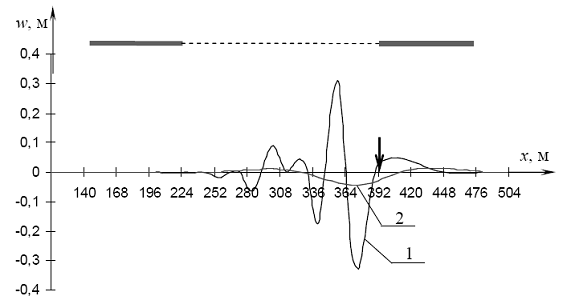
Рис. 4.57. Прогибы при проходе силы Р через точку C₃: 1 - при наличии майны (l = 168 м), 2 - для сплошного льда

.

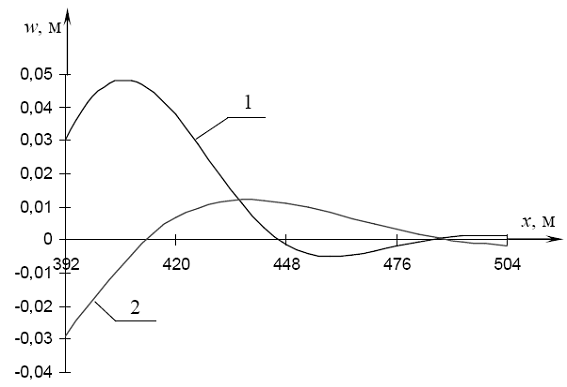
Рис. 4.58. Прогибы льда при проходе силы Р через точку C₃: 1 - при наличии майны (l = 168 м), 2 - для сплошного льда