Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
РАСПРЕДЕЛЕНИЕ ЖИВЫХ ВЕТВЕЙ В МУТОВКАХ ЕЛИ (А.О. Петренко, аспирант)
По данным статьи [1] о численности ветвей
в мутовках кроны ели разных классов роста были получены закономерности, характеризующие качество роста всего ельника по учетным деревьям в зависимости от высоты 
расположения мутовки ели от шейки корня.
Например, для мутовок ели получены модели (рис. 1 и табл. 1):
- первого класса роста
, (1)
,
, 
,
,
;
- третьего класса роста
, (2)
,
;
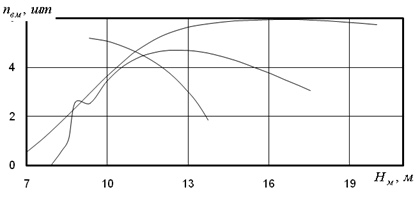
Рис. 1. Графики распределений численности ветвей в мутовках ели
различного класса роста: наверху - первого класса; в середине - третьего,
а круто снижается вниз график ели четвертого класса роста
Таблица 1
Изменение численности живых ветвей в мутовке ели, шт.
|
I класс роста (1) |
III класс роста (2) |
IV класс роста (3) |
||||||
|
|
|
Δ,% |
|
|
Δ,% |
|
|
Δ,% |
|
20.02 19.50 18.83 18.20 17.63 17.15 16.66 16.16 15.45 14.72 14.04 13.50 12.99 12.29 11.72 11.03 10.80 9.95 9.28 8.52 7.68 7.00 |
5.73 5.78 5.84 5.88 5.91 5.93 5.94 5.94 5.92 5.88 5.81 5.73 5.62 5.39 5.10 4.62 4.42 3.58 2.85 2.03 1.16 0.53 |
0,14 -0,04 -0,09 -0,16 -0,11 0,00 0,07 0,11 0,07 0,03 -0,10 -0,11 -0,07 0,09 0,07 0,12 -0,02 -0,23 -0,08 0,57 -0,67 0,36 |
17.54 17.12 16.60 16.05 15.48 14.97 14.70 14.20 13.70 13.22 12.81 12.30 11.80 11.23 10.58 9.97 9.36 8.80 8.55 8.30
|
3.04 3.24 3.49 3.74 3.99 4.19 4.29 4.45 4.57 4.66 4.69 4.68 4.61 4.42 4.02 3.41 2.54 2.56 1.08 0.59
|
0,08 0,02 0,07 -0,07 -0,04 -0,10 -0,04 0,01 -0,08 0,12 0,01 -0,05 0,00 -0,06 -0,03 0,09 -0,08 - -0,13 0,15
|
13.74 13.60 13.38 13.18 12.94 12.66 12.32 11.91 11.36 10.82 10.32 9.92 9.32 |
1.84 2.10 2.47 2.77 3.08 3.41 3.75 4.09 4.46 4.74 4.95 5.07 5.18 |
-0,05 -0,05 0,02 0,10 -0,16 0,03 0,07 -0,01 -0,03 -0,12 0,06 0,05 -0,03
|
, м
- четвертого класса роста
, (3)
,
.
Сопоставление конструкций трех формул показывает, что наиболее сложной является уравнение (1), а остальные две модели являются по конструкции его частными случаями. При этом точность математического описания столь высока, что абсолютная погрешность Δ: во-первых, не превышает 0,01 м по высоте мутовок; во-вторых, даже такие малые возмущения имеют волновой характер.
Этот факт указывает на то, что распределение численности ветвей в мутовках по высоте дерева ели вполне может стать экологическим критериям, весьма чувствительным к малейшим изменениям в условиях места произрастания.
Сравнение трех классов роста у популяций деревьев ели показывает, что максимальная относительная погрешность вышеприведенных формул 
не превышает 1 %. При этом чем хуже условия роста и развития дерева, то тем меньше образуется живых ветвей в мутовках на вершине кроны. При этом с ухудшением условий произрастания повышается высота от корневой шейки до первой живой мутовки ели.
У дерева ели первого класса возраста наблюдается наиболее сложная динамика роста дерева и развития структуры кроны по мутовкам.
Смертность по численности ветвей в мутовках с высотой убывает по закону гибели (спада), а у деревьев ели четвертого класса возраста, наоборот, смертность мутовок только нарастает в ходе жизнедеятельности ели. Деревья ели первого класса роста чувствуют себя спокойно, так как отношение 
у них растет медленно. Даже на последней мутовке из живых ветвей численностью 7,677 шт. не появились только 1,958 шт. мертвых в зародышах почек ветвей, фактически образуя мутовку численностью в 5,73 шт., с произрастающими на высоте 20,02 м ствола ветвями. При этом адаптация среднего дерева происходила по колебательному возмущению с двумя максимумами. Поэтому целью дальнейших исследований является изучение проявлений кризисных колебаний в организме дерева, которые должны, по-видимому. совпасть с колебаниями свойств окружающей растущее дерево среды.
А у деревьев ели четвертого класса роста максимальная напряженность уже была на высоте 9,32 м, когда в момент измерений там находилась первая мутовка с живыми ветвями в начале кроны.
Нижние мутовки ели имеют живые и отмершие ветви. Самоочищением дерево сбрасывает неживые ветви, образуя отпад. При этом плотность расположения ветвей в одной мутовке зависит от двух противоположно направленных процессов.
Для деревьев первого класса роста появилась и третья, хотя и малая по биоэнергетике, но решающая в долголетии. Поэтому ель достигла высоты 20,02 м относительно легко, сохраняя и на дальнейшее способность генерирования живых ветвей в последующих мутовках.
Литература
- Старостин, В.А. О распределении ветвей по толщине в кроне ели в лесных культурах / В.А. Старостин // Межвуз. сб. научн. тр. «Лесоводство, лесные культуры и почвоведение». - Л.: ЛТА, 1991. - С.105-109.
- Пат. 2376749 Российская Федерация, МПК A 01 G 23 / 00 (2006.01). Способ анализа ствола и кроны дерева ели / Мазуркин П.М., Попова А.О. (РФ); заяв. и патентообл. Марийск. гос. тех. ун-т. - №2008120469/12; заявл. 22.05.2008; опубл. 27.12.2009.
- Пат. 2376750 Российская Федерация, МПК A 01 G 23 / 00 (2006.01). Способ анализа ствола модельного дерева / Мазуркин П.М., Попова А.О. (РФ); заяв. и патентообл. Марийск. гос. тех. ун-т. - №2008121100/12; заявл. 26.05.2008; опубл. 27.12.2009.