
Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания

Прикладные задачи динамики ледяного покрова
Козин В. М., Жесткая В. Д., Погорелова А. В., Чижиумов С. Д., Джабраилов М. Р., Морозов В. С., Кустов А. Н.,
5.1. Моделирование трещин с помощью идеальных и упругих шарниров
Для упрощения составления глобальной матрицы жесткости системы сетку конечных элементов удобно ориентировать в общей системе координат ![]() . Это снимает необходимость в преобразовании матриц жесткости конечных элементов при переходе от локальной системы координат
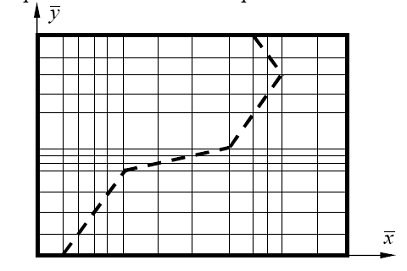
. Это снимает необходимость в преобразовании матриц жесткости конечных элементов при переходе от локальной системы координат![]() конкретного конечного элемента к общей системе координат. Пример построения сетки для пластины со сквозной трещиной, обозначенной пунктирной линией, представлен на рис. 5.1. Как видно из данного рисунка, дискретная модель пластины в общем случае может состоять как из прямоугольных, так и треугольных конечных элементов. Отметим, что минимальные погрешности дискретизации достигаются при использовании квадратных и треугольных конечных элементов с равными боковыми сторонами.
конкретного конечного элемента к общей системе координат. Пример построения сетки для пластины со сквозной трещиной, обозначенной пунктирной линией, представлен на рис. 5.1. Как видно из данного рисунка, дискретная модель пластины в общем случае может состоять как из прямоугольных, так и треугольных конечных элементов. Отметим, что минимальные погрешности дискретизации достигаются при использовании квадратных и треугольных конечных элементов с равными боковыми сторонами.
 .
.
Рис. 5.1.
Сложная геометрическая конфигурация системы сквозных трещин, возникающих в сплошном ледяном покрове, может быть упрощена системой прямолинейных отрезков. Конечно элементная сетка должна формироваться с тем расчетом, чтобы соответствующие узлы располагались точно на отрезках, аппроксимирующих геометрическую конфигурацию системы сквозных трещин, причем для упрощения алгоритма построения сетки желательно, чтобы проекции любой пары отрезков на координатные оси ![]() накладывались друг на друга не более одного раза, т.е. допускается наложение двух произвольно выбранных отрезков, задающих трещину, либо в проекции на ось
накладывались друг на друга не более одного раза, т.е. допускается наложение двух произвольно выбранных отрезков, задающих трещину, либо в проекции на ось ![]() , либо в проекции на ось
, либо в проекции на ось ![]() , но не одновременно. В данном разделе рассмотрен случай использования конечных элементов, узлы которых имеют по четыре локальные степени свободы:
, но не одновременно. В данном разделе рассмотрен случай использования конечных элементов, узлы которых имеют по четыре локальные степени свободы:
![]() ,
, 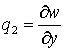 ,
, ![]() ,
, 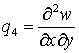 .
.
Принято, что берега прямолинейного участка сквозной трещины при деформации ледяного покрова не расходятся в плоскости пластины и не смещаются друг относительно друга в направлении оси ![]() (перпендикулярно срединной плоскости пластины), т.е. кромки двух смежных контактирующих берегов трещины имеют одинаковые прогибы. Отсюда следует, что углы поворота смежных контактирующих берегов прямолинейного участка сквозной трещины вокруг оси перпендикулярной этому отрезку одинаковы. В то же время углы поворота берегов сквозной трещины вокруг прямолинейного отрезка, ее задающего, отличны. Поэтому в узлах сетки, лежащих на прямолинейных отрезках, задающих положение трещины, вместо узловых перемещений
(перпендикулярно срединной плоскости пластины), т.е. кромки двух смежных контактирующих берегов трещины имеют одинаковые прогибы. Отсюда следует, что углы поворота смежных контактирующих берегов прямолинейного участка сквозной трещины вокруг оси перпендикулярной этому отрезку одинаковы. В то же время углы поворота берегов сквозной трещины вокруг прямолинейного отрезка, ее задающего, отличны. Поэтому в узлах сетки, лежащих на прямолинейных отрезках, задающих положение трещины, вместо узловых перемещений 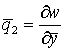 и
и![]() целесообразно вводить узловые перемещения
целесообразно вводить узловые перемещения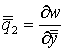 и
и![]() в системе координат
в системе координат ![]() , повернутой относительно общей системы координат
, повернутой относительно общей системы координат![]() . При этом оси
. При этом оси![]() и
и ![]() направлены, соответственно, перпендикулярно и параллельно отрезку, задающему трещину, а ось
направлены, соответственно, перпендикулярно и параллельно отрезку, задающему трещину, а ось ![]() совпадает по направлению с осью
совпадает по направлению с осью ![]() (рис. 5.2). Узловые перемещения
(рис. 5.2). Узловые перемещения![]() и
и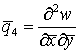 оставляем ориентированными в общей системе координат. Передформированием глобальной матрицы жесткости системы необходимо выполнить преобразование матрицы жесткости конечного элемента, имеющего узел, в котором степени свободы
оставляем ориентированными в общей системе координат. Передформированием глобальной матрицы жесткости системы необходимо выполнить преобразование матрицы жесткости конечного элемента, имеющего узел, в котором степени свободы![]() и
и![]() ориентированы в повернутой системе координат относительно общей системы координат.
ориентированы в повернутой системе координат относительно общей системы координат.
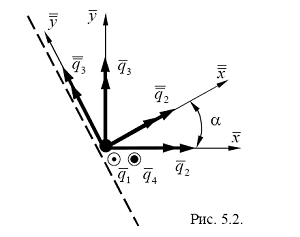 .
.
Координаты точки в локальной системе координат конкретного конечного элемента выражаются через ее координаты в общей системе координат следующим образом:
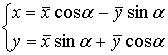 (5.1)
(5.1)
Следовательно,
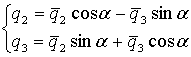 (5.2)
(5.2)
Тогда, связь между векторами узловых перемещений для такого узла в локальной и общей системе координат будет иметь вид:
![]() ,
,
где![]() - матрица направляющих косинусов,
- матрица направляющих косинусов,
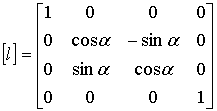 (5.3)
(5.3)
Таким образом, матрица жесткости ![]() конечного элемента, хотя бы в одном узле которого действуют узловые перемещения
конечного элемента, хотя бы в одном узле которого действуют узловые перемещения ![]() и
и ![]() , заданные в повернутой системе координат, должна быть преобразована следующим образом:
, заданные в повернутой системе координат, должна быть преобразована следующим образом:
![]() , (5.4)
, (5.4)
где ![]() - матрица преобразования. Матрица
- матрица преобразования. Матрица ![]() получается последовательным размещением на ее диагонали трех или четырех (по количеству узлов элемента) квадратных матриц четвертого порядка, каждая из которых является либо единичной в случае, если направление узловых перемещений соответствующего узла совпадает с направлением локальных узловых перемещений элемента, либо матрицей
получается последовательным размещением на ее диагонали трех или четырех (по количеству узлов элемента) квадратных матриц четвертого порядка, каждая из которых является либо единичной в случае, если направление узловых перемещений соответствующего узла совпадает с направлением локальных узловых перемещений элемента, либо матрицей ![]() в случае, если направление узловых перемещений соответствующего узла повернуто по отношению к направлению локальных узловых перемещений на угол
в случае, если направление узловых перемещений соответствующего узла повернуто по отношению к направлению локальных узловых перемещений на угол ![]() . Например, если узловые перемещения
. Например, если узловые перемещения ![]() и
и ![]() , соответствующие второму типовому узлу четырехугольного элемента, заданы в системе координат, повернутой на угол α, по отношению к локальной системе координат элемента, то матрица
, соответствующие второму типовому узлу четырехугольного элемента, заданы в системе координат, повернутой на угол α, по отношению к локальной системе координат элемента, то матрица ![]() будет иметь вид:
будет иметь вид:
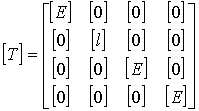 (5.5)
(5.5)
где![]() - единичная матрица четвертого порядка.
- единичная матрица четвертого порядка.
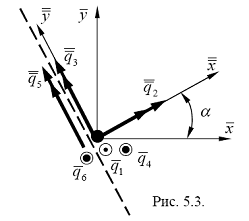
Покажем, что при использовании вышеупомянутых конечных элементов, количество узловых перемещений в узле, расположенном на сквозной трещине, должно равняться шести. Рассмотрим окрестность узла, лежащего на трещине (рис. 5.3). Линия трещины делит окрестность узла на две области. Формально, для конечных элементов, лежащих в первой области, в данном узле должны быть введены четыре степени свободы.
 .
.
Аналогично для конечных элементов, лежащих во второй области, также должны быть введены четыре степени свободы. Но согласно предположению о том, что берега трещины имеют одинаковые прогибы и углы поворота вокруг оси, перпендикулярной отрезку, задающему положение трещины, узловые перемещения ![]() и
и 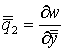 совпадают для обеих областей. Следовательно, четырем локальным степеням свободы в данном узле, которые относятся к элементам, расположенным по одну сторону сквозной трещины, соответствуют глобальные степени свободы
совпадают для обеих областей. Следовательно, четырем локальным степеням свободы в данном узле, которые относятся к элементам, расположенным по одну сторону сквозной трещины, соответствуют глобальные степени свободы ![]() , а четырем локальным степеням свободы в данном узле, которые относятся к элементам, расположенным по другую сторону сквозной трещины -
, а четырем локальным степеням свободы в данном узле, которые относятся к элементам, расположенным по другую сторону сквозной трещины - ![]() . Эта особенность, естественно, должна быть учтена в матрице индексов. Таким образом, в рамках допущенных предположений, в узлах конечноэлементной сетки, лежащих на трещине, должно быть введено шесть глобальных узловых перемещений:
. Эта особенность, естественно, должна быть учтена в матрице индексов. Таким образом, в рамках допущенных предположений, в узлах конечноэлементной сетки, лежащих на трещине, должно быть введено шесть глобальных узловых перемещений:![]() .
.
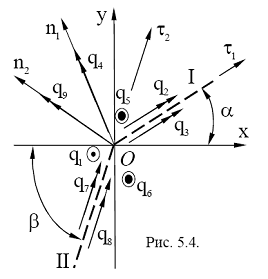
Рассмотрим случай, когда прямолинейный участок трещины меняет свое направление, т.е. имеет место излом линии сквозной трещины (рис. 5.4).
 .
.
Определим количество и направление узловых перемещений, необходимых для точного описания деформированного состояния пластины в рамках используемой математической модели, для узла, расположенного в точке излома. Так как в рассматриваемом узле сходятся два прямолинейных отрезка, задающих трещину, введем две системы координат: одну - ![]() , направив ось
, направив ось ![]() вдоль отрезка I, а ось
вдоль отрезка I, а ось ![]() перпендикулярно ему, другую -
перпендикулярно ему, другую - ![]() , направив ось
, направив ось ![]() вдоль отрезка II, а ось
вдоль отрезка II, а ось ![]() перпендикулярно ему (рис. 3.4). В точке излома введем узловые перемещения:
перпендикулярно ему (рис. 3.4). В точке излома введем узловые перемещения: ![]() - прогиб,
- прогиб, ![]() и
и ![]() - углы поворота смежных берегов трещины, задаваемой отрезком I,
- углы поворота смежных берегов трещины, задаваемой отрезком I, ![]() - угол поворота вокруг оси
- угол поворота вокруг оси ![]() ,
, ![]() и
и ![]() - вторые смешанные производные по одну и другую сторону от трещины,
- вторые смешанные производные по одну и другую сторону от трещины, ![]() и
и ![]() - углы поворота смежных берегов трещины, задаваемых отрезком II,
- углы поворота смежных берегов трещины, задаваемых отрезком II, ![]() - угол поворота вокруг оси . Введенные узловые перемещения имеют следующее математическое выражение:
- угол поворота вокруг оси . Введенные узловые перемещения имеют следующее математическое выражение:
![]() ,
,
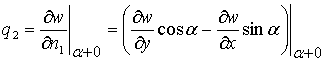 ,
,
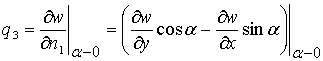 ,
,
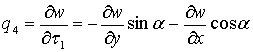 ,
,
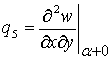 ,
,
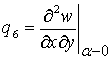 ,
,
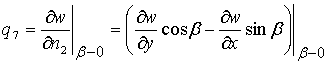 ,
,
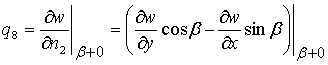 ,
,
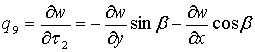 . (5.6)
. (5.6)
Рассмотрим окрестность узла по левую сторону ломаной, задающей сквозную трещину (рис. 5.5), и выразим узловые перемещения ![]() и
и![]() через
через![]() и
и![]()
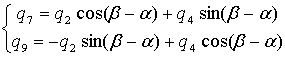 (5.7)
(5.7)
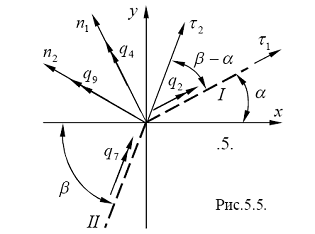 .
.
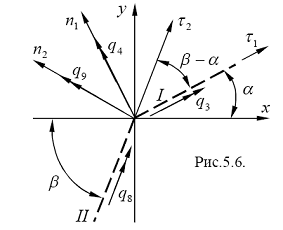
Рассмотрим окрестность узла по правую сторону ломаной, задающей сквозную трещину (рис. 5.6), и выразим узловые перемещения![]() и
и ![]() через
через ![]() и
и![]()
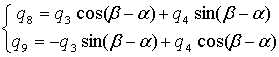 (5.8)
(5.8)
 .
.
Уравнения (5.7) и (5.8) одновременно возможны только при ![]() . Но тогда и
. Но тогда и ![]() . Следовательно, пластина в узле ведет себя как целая. Поэтому, можно считать, что и
. Следовательно, пластина в узле ведет себя как целая. Поэтому, можно считать, что и ![]() . В результате можно сделать вывод, что в точке излома линии сквозной трещины достаточно иметь четыре узловых перемещения
. В результате можно сделать вывод, что в точке излома линии сквозной трещины достаточно иметь четыре узловых перемещения ![]() в исходной общей системе координат.
в исходной общей системе координат.
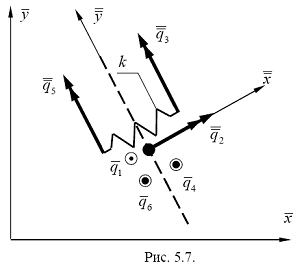
Необходимо отметить, что введение в соответствующем узле шести узловых перемещений по вышеизложенной методике представляет собой моделирование сквозной трещины идеальным цилиндрическим шарниром вдоль линии трещины. В случае линейной зависимости изгибающего момента, действующего на берега трещины в контактном сечении от угла раскрытия трещины, учесть контактное взаимодействие её берегов можно добавляя в глобальную матрицу жесткости системы дополнительную матрицу жесткости формального конечного элемента, связывающего упругой связью узлы, в которых возникают узловые перемещения ![]() и
и![]() (рис. 5.7). Матрица жесткости такого элемента будет иметь вид:
(рис. 5.7). Матрица жесткости такого элемента будет иметь вид:
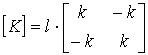 (5.9)
(5.9)
где ![]() - коэффициент пропорциональности между углом раскрытия сквозной трещины и возникающим в контактном сечении погонным изгибающим моментом;
- коэффициент пропорциональности между углом раскрытия сквозной трещины и возникающим в контактном сечении погонным изгибающим моментом;
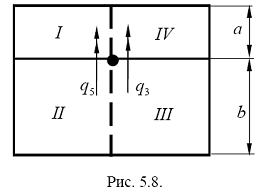
![]() - эффективная длина зоны взаимодействия берегов трещины, приходящаяся на данный узел конечноэлементной сетки (например, для узла, изображенного на рис. 5.8,
- эффективная длина зоны взаимодействия берегов трещины, приходящаяся на данный узел конечноэлементной сетки (например, для узла, изображенного на рис. 5.8, ![]() ).
).
 .
.
Коэффициент пропорциональности между изгибающим моментом и углом раскрытия сквозной трещины характеризует степень сопротивления раскрытию ее берегов. Он может быть использован для выполнения уточненных расчетов с моделированием сквозных трещин упругими шарнирами в отличие от использования идеальных шарниров при численном решении задачи о напряженно-деформированном состоянии ледяного покрова, находящегося под действием движущейся нагрузки.
 .
.