
Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
СПОСОБ ИСПЫТАНИЯ ГОДИЧНЫХ СЛОЕВ ДЕРЕВА (Л.Ю. Варсегова, соискатель)
Динамика [1, 3, 4] радиуса ствола сосны по годичным слоям была изучена на керне древесины, начиная с 1948 по 1992 годы на каждом годичном слое. Дерево произрастало в сосново-березовом насаждении с примесью ели и осины естественного происхождения. Состав пород 9С + 1Б (единичные Е + Ос); тип лесорастительных условий - А2; тип леса - сосняк зеленомошниковый; полнота - 0,8.Для измерений ширины годичных слоев использовался керн комнатно-сухой влажности [2], взятый в 2000 году на высоте 1,3 м. Возраст подроста на высоте 1,3 м составлял 11 лет.
Замеры проводились, начиная с 22 по 66 год жизни дерева. Полный же возраст дерева составляет 74 года (рис. 1).
Из схемы на рис. 1 видно существующими способами, например, с использованием измерительной лупы, что первые 10 лет попадали в сердцевину и не могли быть измеренными из-за малых значений ширины годичных слоев. Поэтому рабочая часть керна начинается с 22 г. и завершается, не доходя до камбиального слоя на 8 лет.
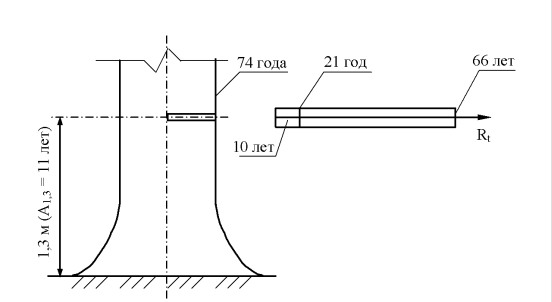
Рис. 1. Схема взятия керна
Поэтому отрезок керна на последних годичных слоях также не был измерен из-за малости ширины и поврежденности буром годичных слоев.
Измерять ширину годичных слоев (или же считать их число) приянто, начиная от периферии к сердцевине. В предлагаемом способе лучше всего измерять от сердцевины к периферии, причем с применением более точных методов измерения можно учитывать и нерабочие зоны керна - присердцевинную и заболонную зону.
Если отсутствует подрост для определения возраста до места взятия керна, то придется брать керн и на корневой шейке дерева.
Для замеров был выбран керн с минимальными углами наклона годичных слоев в продольно-радиальной и радиально-тангенциальной плоскости анизотропии. Ширина годичного слоя измерялась с точностью 0,05 мм при начальном слое, равном 22 году жизни дерева.
Полученные данные были обработаны в математической среде CurveExpert-1.3 (рис. 2) и получена статистическая формула вида:
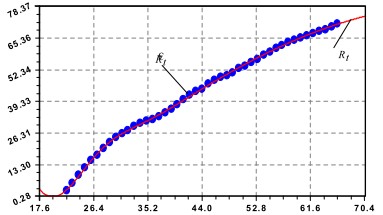
Рис. 2. График динамики радиуса ствола сосны по годичным слоям керна
![]()
![]() , (1)
, (1)
где Rt - расчетный радиус дерева по годичным слоям в направлении от сердцевины к периферии, мм; t - время жизни дерева до взятия керна, с учетом возраста годичных слоев от корневой шейки, лет.
Период колебательной адаптации растущего дерева к месту своего произрастания равен 10,75915 х 2 = 21,6 лет. Причем сдвиг начала волны происходит через 6,13388 радиан, то есть через почти 21 год после начала жизни изучаемого дерева сосны. По лесоводственным данным можно узнать, что происходило в это время, то есть в 2000 - 74 + 21 = 1947 г. Сама сосна появилась в 2000 - 74 = 1926 году, по-видимому, после крупных лесных пожаров 1921 г.
По измеренным значениям ширины годичных слоев можно составить статистические закономерности роста каждого учетного дерева без его валки и одномоментного уничтожения в виде модельного дерева. Сохранение жизнедеятельности испытуемому дереву чрезвычайно важно для прогнозирования и последующей повторной идентификации по результатам дополнительных замеров, например по керну, взятом в последующих годах. Одно дерево может выдержать взятие до 10-12 кернов на разных местах по высоте ствола, поэтому исследование на одном растущем дереве можно продолжать долгое время. На ценных деревьях керны берутся на крупных ветвях.
Доверительная вероятность модели (1) будет равна не меньше 100 - 7,35 = 92,65%, что позволяет дать долгосрочный прогноз, равный длине основания прогноза 1992 - 1948 = 44 года, по которому на рис. 3 был построен график в программной среде Excel.
Горизонт прогноза показывает на перспективу изменение показателя, то есть переменного радиуса ствола сосны на высоте 1,3 м.
А глубина основания прогноза показывает ретроспективу значений показателя до момента зарождения дерева, то есть до 1926 г. В горизонте прогноза по графику на рисунке 2 можно видеть, что максимальное значение 79,9 мм радиус ствола сосны по формуле (1) достигнет к 87 годам, то есть к 2013 году.
Дальнейший радиальный прирост станет убывать, то есть дерево с 87 летнего возраста начнет умирать и засыхать по толщине.
Предлагаемый способ является универсальным и одновременно простым в практической реализации. Он позволяет реализовать физико-технологический подход к экологической, экономической и комплексной эколого-экономической оценки территорий.
Взятие кернов на одном и том же учетном дереве через определенные периоды позволяет наладить экологический мониторинг.
Литература
- Мазуркин, П.М. Дендрометрия. Статистическое древоведение / П.М. Мазуркин. - Учебное пособие. - Ч. 1. - Йошкар-Ола: МарГТУ, 2003. - 308 с.
- Колесникова, А.А. Исследование свойств древесины по кернам: научное издание / А.А. Колесникова. - Йошкар-Ола: МарГТУ, 2002. - 178 с.
- Мазуркин, П.М. Испытание растущего дерева / П.М. Мазуркин, Л.Ю. Варсегова // Успехи совр. естествознания. - 2010. - № 4. - С.38-43. 0,40 п.л.
- Мазуркин, П.М. Измерение ширины годичного слоя на керне древесины / П.М. Мазуркин, Л.Ю. Варсегова // Успехи современного естествознания. - 2010. - № 4. - С.31-37. 0,45 п.л.
