
Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
АСИММЕТРИЧНЫЕ СИГНАЛЫ ЭЛЕКТРОКАРДИОГРАММЫ (П.М. Мазуркин, А.А. Васильев, специалитет (ИМБП-51))
Цель - получение математической модели ЭКГ сигнала. Задан один период электрокардиографического сигнала без патологии в системе отсчетаИзмеренный сигнал показан на рисунке 1.
Требуется определить:
1) табличную модель ЭКГ сигнала;
2) математическую модель в виде нелинейного уравнения на основе табличной модели;
3) оценку адекватности модели.
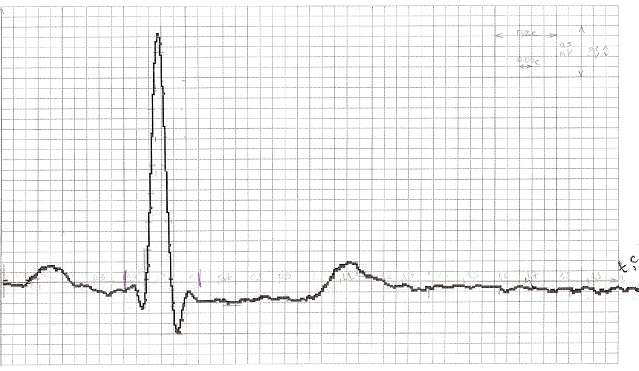
Рис. 1. Сетка для измерений сигнала сердца
Табличную модель обычно представляют в двух видах - в программе Excel и текстовом редакторе Word через координатные точки в принятой системе отсчета. Большинство табличных моделей, как исходный объект для последующего статистического моделирования, оформляется в среде Excel.
Данные в таблице 1 показаны без сортировки дублирующих значения напряжения сердца.
|
Таблица 1 Табличная модель ЭКГ сигнала сердца
|
Для получения математической модели осуществляется процесс идентификации асимметрчных вейвлет-функций проф. П.М. Мазуркина.
Массив табличной модели внвчале сортируется для усорения моделирования, а затем копируется в программную среду CurveExpert-1.3, где и выполняется статистическое моделирование в готовую математическую модель.
Процедура моделирования начинается с простейшей формулы (с биотехнического закона), где проводится произвольный выбор параметров (коэффициентов) уравнения. Затем пошагово усложняем модель до полноты конструкции. По мере усложнения формулы из предыдущего сеанса поиска принимаются все более точные записи коэффициентов (параметров модели). Завершается процесс сложным нелинейным многсленным уравнением. Полученное уравнение будет являться математической моделью данного ЭКГ сигнала.
На рисунке 2, по методике прямого фрактального аналаиза, привееден график начал работы предсердия.
Графический результат U(t) двухчленной модели, соответствующий комплексу QRS сердца, приведен на рисунке 3.
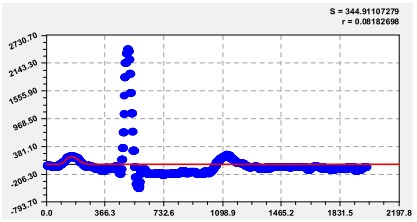
Рис. 1. Модель начала работы предсердия здорового человека
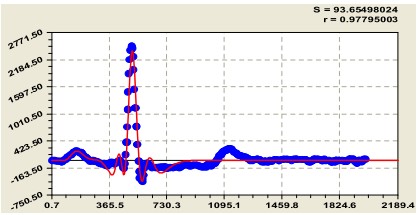
Рис. 2. Модель работы предсердия и желудочка сердца у здорового человека
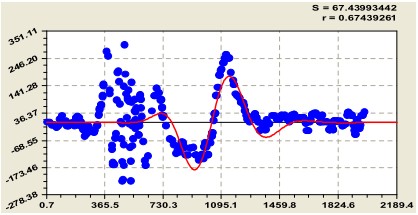
Рис. 3. Модель работы предсердия после желудочка сердца у здорового человека
Графический результат U(t) по остаткам от модели на рисунке 2, оответствующий зубцу Т сигнала электрокардиограммы сердца здорового человека, показан на рисунке 3.
С пятой составляющей по тридцать третью отображаются новые асимметричные вейвлет-функции, но их принадлежность колебанифм сердечных мышц неявная. По-видимому, графики импульсных значений напряжения электрических сигналов могут принадлежать другим органам человека.
После завершения всех процедур статистического моделирования записываем математическое уравнение (общую закономерность)
![]() , (1)
, (1)
![]() .
.
Парамеры модели и коэффициент корреляции привеедны в таблице 2.
Таблица 2
Параметры математической модели ЭКГ сердца без патологии
|
i |
Амплитуда колебания, мВ |
Полупериод и сдвиг колебания, мс |
Коэфф. корр. |
||||||
|
a1i |
a2i |
a3i |
a4i |
a5i |
a6i |
a7i |
a8i |
||
|
1 |
2.59574e-028 |
16.74766 |
0.078955 |
1.04811 |
0 |
0 |
0 |
0 |
0.9780 |
|
2 |
1.42992e-149 |
63.76683 |
0.013904 |
1.30529 |
10.59449 |
0.0022405 |
1.34410 |
3.18773 |
|
|
3 |
-3.40070e-033 |
14.31631 |
0.000120 |
1.77400 |
21.15976 |
0.21683 |
0.87313 |
0.52152 |
|
|
4 |
-1.67937e-064 |
25.57819 |
0.021603 |
1.01816 |
244.7042 |
0.0030608 |
0.98941 |
5.23804 |
0.674 |
Первые три составляющие доставляют общий коэффиент кореляции 0,9780. Поэтому уравнение (1) вполне достаточное для того, чтобы облегчить кардиологу диагностику сердца по электрокардиомме.
Для удобства анализа электрокардиограммы в медицине принято обозначать зубцы ЭКГ латинскими буквами. Если амплитуда зубца составляет больше 20% от размаха электрокардиосигнала, то этот зубец обозначают прописной (заглавной буквой).
Если же амплитуда зубца меньше 20%, то для его названия используют строчную (малую) букву. Главным зубцам на ЭКГ присвоены обозначения P, Q, R, S, T, U (рис. 4).
Каждый зубец отражает деполяризацию или реполяризацию определенной области сердца. Изменения вольтажа, регистрируемые электрокардиографом, очень малы - порядка нескольких милливольт. Размер каждого зубца соответствует уровню вольтажа, генерируемого конкретным явлением. Рассмотрим это более подробно.
После статистического моделирования общая закономерность составляющих, как с нормальным сигналом, будет состоять из законов показательного роста и экспоненциальной гибели, и для комплекса QRS с сегментами PQ и ST из волнового вейвлет-сигнала (табл. 3-5).
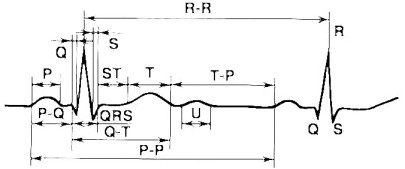
Рис. 4. Стандартная форма записи ЭКГ [1]
Таблица 3
Параметры модели абберантной предсердной экстрасистолы
|
i |
Амплитуда колебания, мВ |
Полупериод и сдвиг колебания, с |
Коэфф. коррел. |
||||||
|
a1i |
a2i |
a3i |
a4i |
a5i |
a6i |
a7i |
a8i |
||
|
1 |
3.39097e-022 |
16.50379 |
0.74900 |
0.72455 |
0.5t |
0 |
0 |
0 |
0.9762 |
|
2 |
2.36562e-148 |
71.50751 |
0.13395 |
1.07389 |
4.57805 |
0.03342 |
1.03638 |
0.22334 |
|
|
3 |
-3.32399e-126 |
62.36981 |
0.20288 |
1 |
26.40615 |
0 |
0 |
-2.34372 |
|
|
4 |
2.50364e-151 |
61.69093 |
0.01326 |
1.26758 |
0.5t |
0 |
0 |
0 |
|
Таблица 4
Параметры модели предсердной тахикардии
|
i |
Амплитуда колебания, мВ |
Полупериод и сдвиг колебания, с |
Коэфф. коррел. |
||||||
|
a1i |
a2i |
a3i |
a4i |
a5i |
a6i |
a7i |
a8i |
||
|
1 |
1.39320e-009 |
6.02345 |
0.00040 |
1.82651 |
0.5t |
0 |
0 |
0 |
0.9750 |
|
2 |
-1.43267e-142 |
66.65493 |
0.01384 |
1.42567 |
116.1773 |
168.61888 |
-0.19249 |
0.07823 |
|
|
3 |
3.17384e-138 |
68.64574 |
0.22979 |
1 |
3.57298 |
0 |
0 |
-3.80494 |
|
|
4 |
2.25435e-139 |
58.58918 |
0.01281 |
1.29241 |
0.5t |
0 |
0 |
0 |
|
Таблица 5
Параметры модели депрессии сегмента ST
|
i |
Амплитуда колебания, мВ |
Полупериод и сдвиг колебания, с |
Коэфф. коррел. |
||||||
|
a1i |
a2i |
a3i |
a4i |
a5i |
a6i |
a7i |
a8i |
||
|
1 |
0.93714 |
1.57996 |
0.00021 |
2.06734 |
0.5t |
0 |
0 |
0 |
0.9833 |
|
2 |
-5.53434e-106 |
60.06181 |
0.19442 |
1.11188 |
113.6701 |
-0.96305 |
0.76804 |
4.24208 |
|
|
3 |
5.48499e-142 |
64.52447 |
0.01347 |
1.39195 |
0.5t |
0 |
0 |
0 |
|
Полученная математическая модель сигнала с депрессией сегмента ST состоит из трех составляющих, так как графическая модель комплекса QRS с сегментами PQ и ST имеет существенное сходство с исходным сигналом (рис. 5).
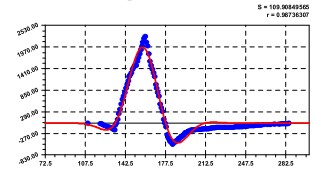
Рис. 5. Точки - исходный сигнал, сплошная - модель
Оказалось, в сигнале со стволовым ритмом зубец P экстрасистолы отсутствует, поэтому составляющего нет в формуле, как и по остаткам комплекса QRS с сегментами TQ и ST. Это связано с высоким значением коэффициента корреляции основного сигнала. Фрактально мелкие сигналы идентифицируются составляющими.
