
Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания

Прикладные задачи динамики ледяного покрова
Козин В. М., Жесткая В. Д., Погорелова А. В., Чижиумов С. Д., Джабраилов М. Р., Морозов В. С., Кустов А. Н.,
5.3.2. Обоснование выбора способа моделирования сквозной трещины в ледяном покрове\
Рассмотрим проблему выбора способа моделирования сквозной трещины в ледяном покрове при численном решении задач методом, изложенным в [38]. Как отмечено в разделе 5.1, в рамках используемой математической модели возможны, по крайней мере, два способа моделирования сквозных трещин в ледяном покрове: идеальными цилиндрическими шарнирами и упругими шарнирами. Выполним оценку двух этих способов на конкретном примере.
Рассмотрим задачу о движении сосредоточенной нагрузки по прямоугольной ледяной пластине с прямолинейной сквозной трещиной, пересекающей пластину по всей её ширине (рис.5.32). Пластина имеет длину Lx и ширину Ly. Пластина жестко заделана по контуру. При дискретизации она разбивалась на квадратные конечные элементы со стороной a = 25 м.В начальный момент времени сосредоточенная сила P находится в состоянии покоя на оси x, отстоит от края пластины на расстоянии L0 и мгновенно приобретает постоянную скорость v. Нагрузка движется вдоль оси x. Трещина параллельна оси y и находится на расстоянии L1 от края пластины.
В первой серии расчетов сквозная трещина моделировалась идеальными цилиндрическими шарнирами. Рассматривался ряд пластин с размерами Lx = 1500 м, Ly = 200 м и толщинами h = 0,2; 0,5; 0,7, 1,0 м. Скорость движения нагрузки v во всех расчетах составляла 5 м/с.
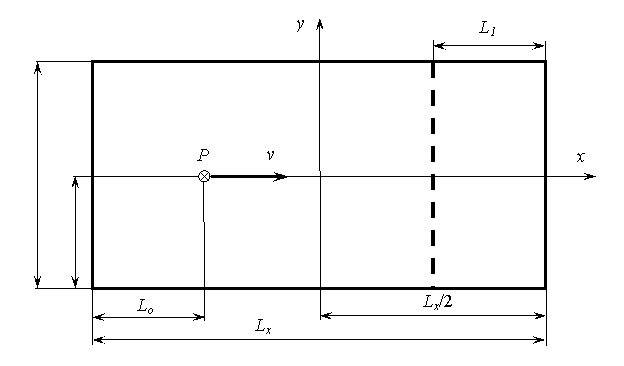
Рис. 5.32. Расчетная схема задачи
Рассчитывалось движение нагрузки в течение времени равном 200 с. Параметры, определяющие начальное положение нагрузки и положение трещины, имели следующие значения: L0 = 250 м; L1 = 350 м. Другие параметры задачи имели “стандартные” значения, за исключением одной особенности: для каждой толщины льда подбиралась такая величина нагрузки, чтобы в пластине возникали напряжения, близкие к критическим. За критическое напряжение принималось σв = 0,8 МПа (усреднённое значение временного напряжения для пресного льда). Таким образом, мы сможем оценить поведение сквозных трещин в условиях критического напряженно-деформированного состояния ледяной пластины. Для толщин льда h = 0,2; 0,5; 0,7; 1,0 м величина нагрузки имела соответствующие значения P = 0,7·105; 0,25·106; 0,4·106; 0,8·106 Н. В результате выполнения расчетов, получили, что при данных значениях нагрузок для рассматриваемых толщин льда, в режиме установившегося движения (момент времени t = 100 c) нормальные напряжения σx в пластине, действительно достигают критических значений 0,8-1,0 МПа (рис. 5.33). Соответствующие нормальные напряжения σy в пластине имеют несколько меньшие значения, порядка 0,6-0,8 МПа (рис. 5.34). В момент времени t = 180 с, когда нагрузка находится непосредственно на трещине (x = 400 м), напряжения σx падают до нуля, а напряжения σy несколько возрастают (рис. 5.35). Коэффициент kσy увеличения напряжений σy при прохождении нагрузкой трещины, по отношению к установившемуся значению напряжений, приведен в таблице 5.3. К моменту времени t = 185 с, когда нагрузка находится в точке с координатой x = 425 м. нормальные напряжения σx возрастают, и достигают значений, несколько больших, чем при установившемся режиме движения (рис. 5.36). Соответствующий коэффициент увеличения kσx также приведен в таблице 5.3.
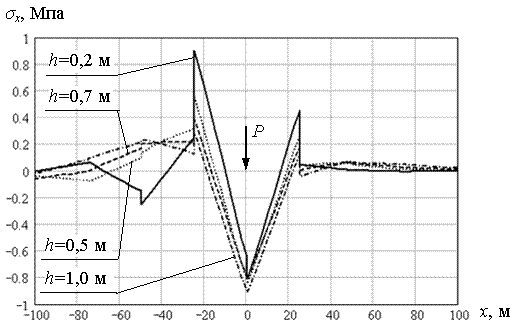
Рис. 5.33. Напряжения σx при установившемся режиме движения
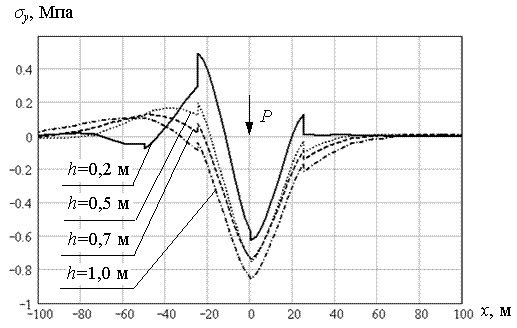
Рис. 5.34. Напряжения σy при установившемся режиме движения
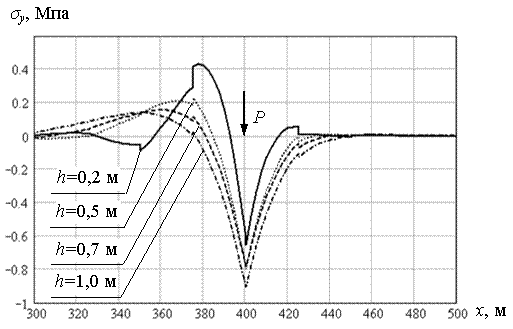
Рис. 5.35. Максимальные значения напряжений σy
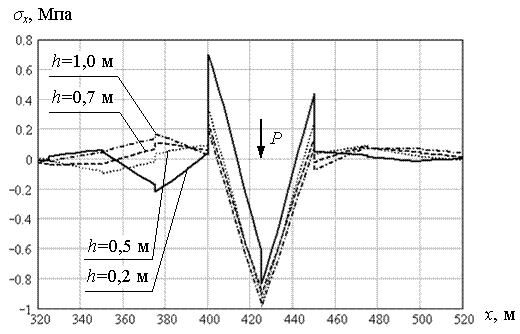
Рис. 5.36. Максимальные значения напряжений σx
Таблица 5.3
| h, м | Пара-метр | Уст. реж. (t = 100 c) | t = 180, с | t = 182, с | t = 185, с | kw | kσx | kσy |
| 0,2 | w, м | 0,018 |
| 0,034 |
| 1,889 | 1,001 | 1,006 |
| σx , МПа | 0,813 |
|
| 0,814 | ||||
| σy , МПа | 0,625 | 0,629 |
|
| ||||
| 0,5 | w, м | 0,023 |
| 0,035 |
| 1,522 | 1,124 | 1,072 |
| σx , МПа | 0,845 |
|
| 0,95 | ||||
| σy , МПа | 0,75 | 0,804 |
|
| ||||
| 0,7 | w, м | 0,025 |
| 0,0365 |
| 1,46 | 1,118 | 1,073 |
| σx , МПа | 0,805 |
|
| 0,9 | ||||
| σy , МПа | 0,738 | 0,792 |
|
| ||||
| 1,0 | w, м | 0,031 |
| 0,045 |
| 1,452 | 1,082 | 1,071 |
| σx , МПа | 0,91 |
|
| 0,985 | ||||
| σy , МПа | 0,854 | 0,915 |
|
|
Величина прогибов достигает максимального значения в момент времени t = 182 с, когда нагрузка P находится на расстоянии 10 м от трещины после её пересечения (x = 410 м). Графики прогибов точек пластины, лежащих на оси x для момента времени t = 182 с, представлены на рис. 5.37.
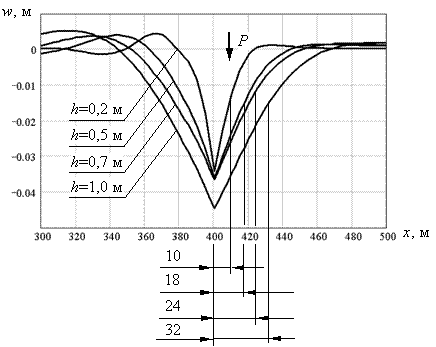
Рис. 5.37. Максимальные прогибы льда в зоне трещины
На серии рисунков 5.38 – 5.41 для рассмотренных толщин льда представлены графики изменения во времени углов поворота левого берега трещины (кривая 1), правого берега (кривая 2) и график изменения угла раскрытия трещины (кривая 3). Из анализа данных графиков, видно, что угол раскрытия трещины принимает максимальное значение также в момент времени t = 182 с, т.е. максимальный прогиб и максимальный угол раскрытия трещины возникают одновременно. Для толщин льда h = 0,2; 0,5; 0,7; 1,0 м максимальные углы раскрытия трещины, в случае её моделирования идеальными шарнирами имели следующие значения 6,637·10-3 ; 3,091·10-3 ; 2,381·10-3 ; 2,21·10-3 рад, соответственно.
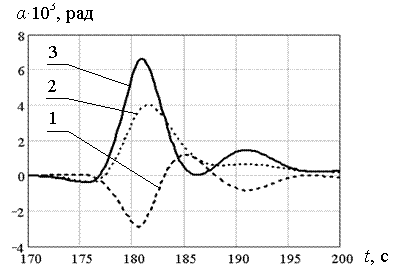
Рис. 5.38. Максимальные углы поворота берегов и раскрытия трещины (h=0,2 м; P=0,7·105 Н)
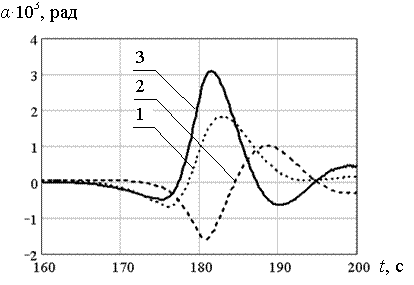
Рис. 5.39. Максимальные углы поворота берегов и раскрытия трещины (h=0,5 м; P=0,25·106 Н)
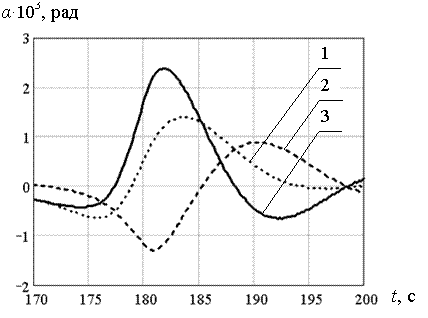
Рис. 5.40. Максимальные углы поворота берегов и раскрытия трещины (h=0,7 м; P=0,4·106 Н)
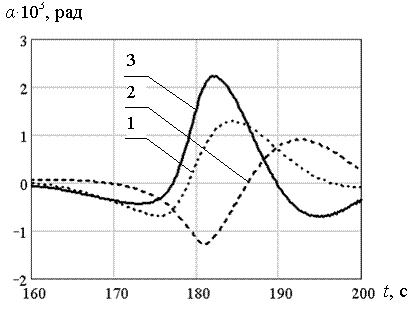
Рис. 5.41. Максимальные углы поворота берегов и раскрытия трещины (h=1,0 м; P=0,8·106 Н)
Отрезок пластины, ограниченный трещиной и точкой перегиба графика прогибов, находится в схожем деформированном состоянии, что и пролет балки-стенки в серии расчетов по определению коэффициента k (см. раздел 5.2). И в точке перегиба графика прогибов пластины, и в шарнирной опоре балки-стенки изгибающий момент равен нулю. Для каждой толщины льда на рис. 5.14 указано характерное расстояние от трещины до ближайшей точки перегиба графика прогибов, в соответствии с которым по графикам 5.19-5.22, приведенными в разделе 5.2, выбираются значения коэффициента погонной жесткости k. Для толщин льда h = 0,2; 0,5; 0,7; 1,0 м имеем следующие длины соответствующих балок-стенок: 10, 18, 24 и 32 м. При этом погрешность линеаризации момента M не будет превышать 5 %, если максимальные углы раскрытия трещины не будут превышать следующие значения: 1,167·10-3; 3·10-3; 2·10-3; 2,5·10-3 рад соответственно толщинам льда h = 0,2; 0,5; 0,7; 1 м (см. таб. 5.1). Таким образом, при толщинах льда h = 0,2; 0,5; 0,7; 1,0 м будем использовать значения коэффициента k = 0,63·106 ; 0,5·107 ; 1,1·107 ; 3,0·107 Н/рад, соответственно. Отметим, что величины определенных таким образом коэффициентов погонной жесткости малы по сравнению с цилиндрическими жесткостями пластин соответствующих толщин. Для h = 0,2 м k = 0.118·D, для h = 0,5 м k = 0.06·D, для h = 0,7 м k = 0.048·D, для h = 1,0 м k = 0.045·D, где D – цилиндрическая жесткость пластины соответствующей толщины.
Во второй серии расчетов трещины моделировались упругими шарнирами. Для всех рассматриваемых толщин льда получено уменьшение величины максимальных прогибов (от 1 до 7 %). Напряжения σx и σy практически не изменились. Максимальные значения расчетных параметров и коэффициенты их отношения для двух разных способов моделирования трещин приведены в таблице 5.4.
Таблица 5.4.
| h, м | Параметр | Идеальный | Упругий | Коэффициент |
| 0,2 | w, м | 0,034 | 0,0331 | 0,974 |
| σx , МПа | 0,814 | 0,808 | 0,993 | |
| σy , МПа | 0,629 | 0,649 | 1,032 | |
| 0,5 | w, м | 0,035 | 0,0346 | 0,989 |
| σx , МПа | 0,95 | 0,953 | 1,003 | |
| σy , МПа | 0,804 | 0,813 | 1,011 | |
| 0,7 | w, м | 0,0365 | 0,0348 | 0,953 |
| σx , МПа | 0,9 | 0,902 | 1,002 | |
| σy , МПа | 0,792 | 0,799 | 1,009 | |
| 1,0 | w, м | 0,045 | 0,042 | 0,933 |
| σx , МПа | 0,985 | 0,986 | 1,001 | |
| σy , МПа | 0,915 | 0,917 | 1,002 |
На рис. 5.42 и 5.43 приведены графики максимальных прогибов и нормальных напряжений в районе трещины в момент пересечении её нагрузкой для случая h = 1,0 м. Здесь сплошные кривые соответствуют случаю моделирования трещины идеальными шарнирами, а точечные кривые – упругими шарнирами. Как видно из рисунков – кривые практически идентичны.
Значения максимальных углов раскрытия берегов трещины в случае её моделирования упругими шарнирами при толщинах льда h = 0,2; 0,5; 0,7; 1,0 м составили следующие значения: 6,438·10-3 ; 3,022·10-3 ; 2,316·10-3 ; 2,139·10-3 рад, соответственно. То есть, в соответствии с данными таблицы 5.1 (см. раздел 5.2), для льда толщиной h = 0,5 и 1 м, расчетные значения максимальных углов раскрытия берегов трещины не превысили предельно допустимых, при которых погрешность линеаризации контактного изгибающего момента не превышает 5-6 %. Для льда толщиной h = 0,2 и 0,7 м это условие не было выдержано, поэтому влияние контактного изгибающего момента M было учтено с несколько большей погрешностью. Отметим, что при меньших расчетных нагрузках углы раскрытия трещины будут меньше, и момент M будет учтен без значительных погрешностей.
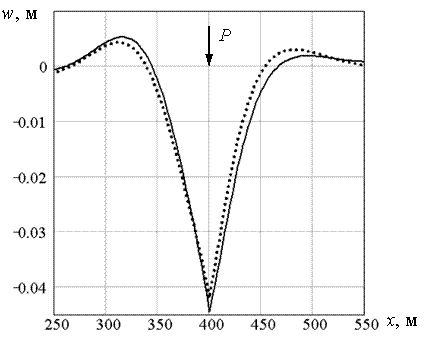
Рис. 5.42. Прогибы пластины при пересечении трещины нагрузкой
Полученные результаты свидетельствуют о том, что учет сил контактного взаимодействия берегов сквозной трещины при её раскрытии в виде моделирования трещин упругими шарнирами оказывает незначительное влияние на рассчитываемые параметры НДС ледяной пластины по сравнению с моделированием трещин идеальными шарнирами. Таким образом, для расчета большинства инженерных задач о движении нагрузки по ледяному покрову, ослабленному сквозной трещиной, достаточно ограничиться учетом трещины в расчетной схеме в виде идеального шарнира.
Выполненные расчеты дают основание полагать, что наличие сквозной трещины в ледяном покрове при её пересечении движущейся нагрузкой может приводить на определённых режимах движения к увеличению максимальных прогибов приблизительно в 1,5 раза и нормальных напряжений σx на 10-12 % (см. таб. 5.3) по сравнению с теми же параметрами НДС при установившемся движении по сплошной пластине.
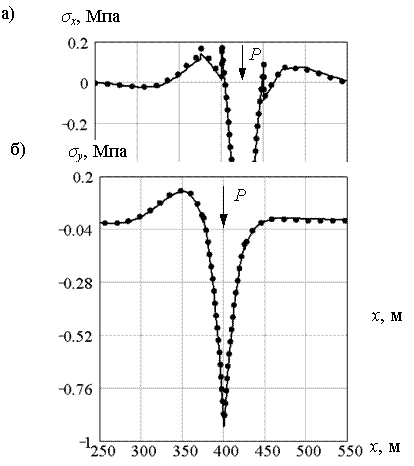
Рис. 5.43. Нормальные напряжения σx (а) и σy (б) при пересечении трещины нагрузкой