
Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания

Прикладные задачи динамики ледяного покрова
Козин В. М., Жесткая В. Д., Погорелова А. В., Чижиумов С. Д., Джабраилов М. Р., Морозов В. С., Кустов А. Н.,
5.3.3. Равномерное прямолинейное движение сосредоточенной нагрузки перпендикулярно сквозной прямолинейной трещине
Исследуем влияние скорости движения нагрузки на величину максимальных прогибов ледяной пластины. Для этого, рассмотрим задачу о движении сосредоточенной нагрузки по прямоугольной ледяной пластине с прямолинейной сквозной трещиной, пересекающей пластину по всей её ширине (рис.5.32). Пластина имеет длину Lx = 1500 м и ширину Ly =200 м. Пластина жестко заделана по контуру. При дискретизации она разбивается на квадратные конечные элементы со стороной a=25 м. В начальный момент времени сосредоточенная сила P = 0,4·106 Н находится в состоянии покоя на оси x, отстоит от края пластины на расстоянии L0 и мгновенно приобретает постоянную скорость v. Нагрузка движется вдоль оси x. Трещина параллельна оси y и находится на расстоянии L1 = 350 м от края пластины. Трещина моделируется идеальными шарнирами.
Была выполнена серия расчетов с варьированием скорости от 0 до 9 м/с с шагом 1 м/с. Значения остальных параметров задачи равны “стандартным”. Для каждой расчетной скорости движения нагрузки подбиралось такое расстояние L0 , что бы обеспечивался стационарный режим движения при пересечении трещины нагрузкой (при v = 2 м/с L0 = 800 м , при v = 9 м/с L0 = 50 м). Рассчитанное поле прогибов участка ледяной пластины при 100<x<600 м в момент времени, когда при пересечении трещины нагрузкой возникают максимальные прогибы (для случая v = 7 м/с поле прогибов представлено на рис. 5.44). Обобщенные результаты расчетов в виде графика зависимости величины максимальных прогибов, которые возникают на трещине в точке с координатой y = 0, от скорости движения нагрузки приведены на рис. 5.45 (кривая 1). Здесь же для сравнения приведен аналогичный график, полученный при тех же параметрах задачи, но для сплошной пластины (кривая 2). Во всем диапазоне рассматриваемых скоростей график “1” лежит выше графика “2”, т.е. максимальные прогибы на трещине при любой скорости движения нагрузки, как и следовало ожидать, больше чем в случае сплошной пластины. Отметим особенность: в случае сплошной пластины резонансный прогиб больше статического, а при наличии трещины максимальные статический и резонансный прогибы, возникающие на трещине, приблизительно одинаковы.
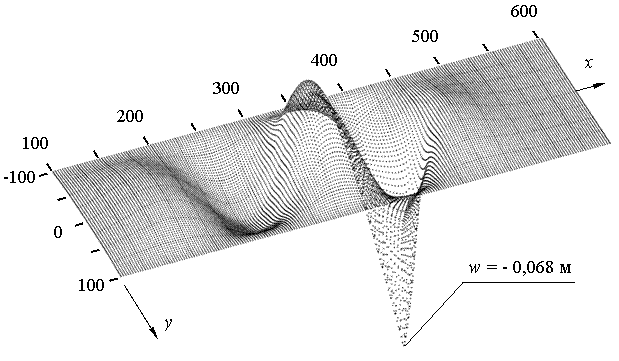
Рис. 5.44. Прогибы ледяной пластины при v = 7 м/с
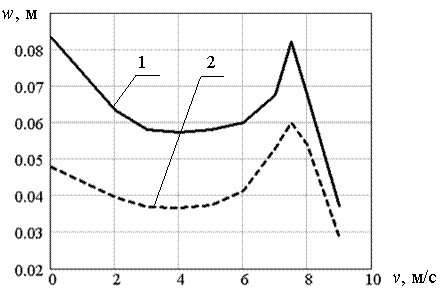
Рис. 5.45. Зависимость величины максимального прогиба от скорости движения нагрузки