
Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания

Прикладные задачи динамики ледяного покрова
Козин В. М., Жесткая В. Д., Погорелова А. В., Чижиумов С. Д., Джабраилов М. Р., Морозов В. С., Кустов А. Н.,
6.2.Техническое обеспечение модельных экспериментов по исследованию ИГВ с применением модели неразрушаемого сплошного льда
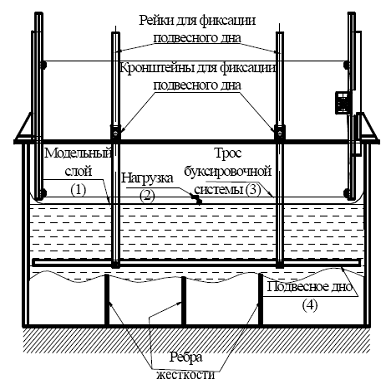
Лабораторная установка представляла собой металлический бассейн, имеющий размеры ![]() м, и заполненный водой (рис. 6.2 –6. 6). При проведении экспериментов на поверхности воды свободно укладывался модельный слой 1 (рис.6.2, 6.3), представлявший собой резиновую пленку толщиной 1 мм. Имитация подвижной нагрузки осуществлялась с помощью ролика 2, приводимого в движение с помощью троса буксировочной системы 3. Изменение глубины водоема, осуществлялось посредством вертикального перемещения подвесного дна 4. Для моделирования влияния на параметры ИГВ берегов использовались две пластины высотой 100 мм, которые устанавливались между подвесным дном и модельным слоем. С помощью датчика перемещений 5 регистрировались профили возбуждаемых ИГВ.
м, и заполненный водой (рис. 6.2 –6. 6). При проведении экспериментов на поверхности воды свободно укладывался модельный слой 1 (рис.6.2, 6.3), представлявший собой резиновую пленку толщиной 1 мм. Имитация подвижной нагрузки осуществлялась с помощью ролика 2, приводимого в движение с помощью троса буксировочной системы 3. Изменение глубины водоема, осуществлялось посредством вертикального перемещения подвесного дна 4. Для моделирования влияния на параметры ИГВ берегов использовались две пластины высотой 100 мм, которые устанавливались между подвесным дном и модельным слоем. С помощью датчика перемещений 5 регистрировались профили возбуждаемых ИГВ.
 .
.
Рис. 6.2 Лабораторная установка (вид сбоку)
 .
.
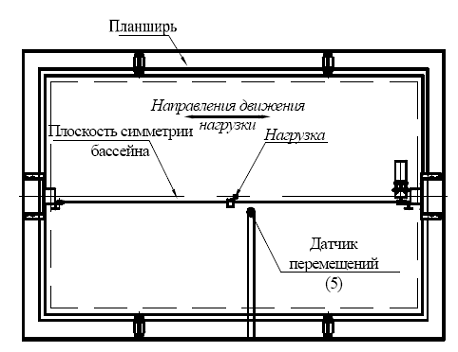
Рис. 6.3 Лабораторная установка (вид сверху).
 .
.
Рис. 6.4 Лабораторная установка (изометрия).
 .
.
Рис. 6.5. Общий вид буксировочной системы
 .
.
Рис.6. 6. Датчик регистрации перемещений модельного слоя
6. 6.3. ###########################################################################################################
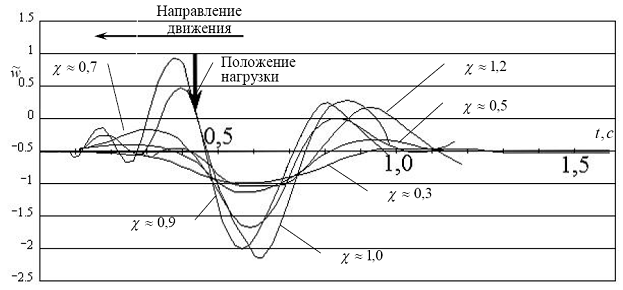
С целью изучения характера возникающих в системе «лед-вода» ИГВ проводилась буксировка ролика 2 с различными скоростями по поверхности модельного слоя 1 с одновременной регистрацией деформаций модельного слоя датчиком 5 (рис.6.2). Использовавшийся датчик позволял регистрировать вертикальные перемещения модельного слоя в заданной точке. В результате были получены профили ИГВ вблизи линии движения нагрузки (рис. 6.7).
 .
.
Рис.6.7. Экспериментальные кривые профилей ИГВ при ![]() .
.
Как показали результаты буксировок, максимальные амплитуды ИГВ соответствовали определенным скоростям движения нагрузки, равным резонансным. В соответствии с теорией волновых движений ледяного покрова, резонансные скорости [124] определяются по следующим формулам:
− для мелкой воды, т.е. при ![]() (
(![]() - волновое число) критическая скорость не зависит от характеристик ледяного покрова и её можно определить по зависимости (6.2).
- волновое число) критическая скорость не зависит от характеристик ледяного покрова и её можно определить по зависимости (6.2).
![]() (6.2),
(6.2),
− для глубокой воды, т.е. при![]()
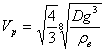 (6.3)
(6.3)
При этом под резонансными принято понимать скорости движения нагрузки ![]() , при которых происходит значительное увеличение амплитуд ИГВ, т.е. возникновение изгибно-гравитационного резонанса (ИГР) [58].
, при которых происходит значительное увеличение амплитуд ИГВ, т.е. возникновение изгибно-гравитационного резонанса (ИГР) [58].
 .
.
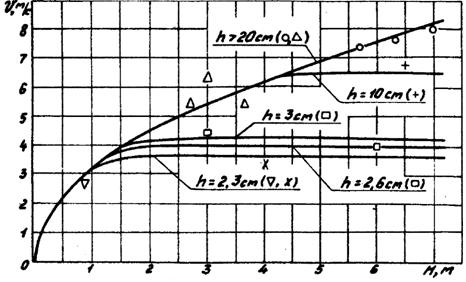
Рис. 8. Значения резонансных скоростей нагрузки в зависимости от глубины воды и толщины льда. (--- теория., , , , - эксперимент).
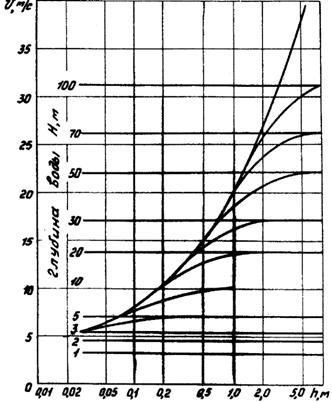
На основе теоретических зависимостей в работе [31] получены значения резонансных скоростей в функции от толщины льда и глубины воды (рис. 6.8). Результаты этих расчетов совпадают с выводами, приведенными в работе [124]. Также на рис. 9. сопоставлены теоретические и экспериментальные данные значений резонансных скоростей, полученные при движении по льду полунатурных и модельных СВП [44]. Эти данные подтверждают справедливость теоретических зависимостей (6.2, 6.3).
 .
.
Рис. 6.9. Сопоставление теоретических и экспериментальных значений резонансных скоростей движения нагрузки.
Таблица 6.1.
Сопоставление теоретических характеристик изгибно-гравитационных волн с экспериментальными данными, полученными для h = 1 м.
| Глубина воды H, м | Скорость движения нагрузки | Длина ИГВ | Период ИГВ | ||||
| Экспе-римент | Пересчет по зависимостям (4.1) | Экспе-римент | Пересчет по зависимостям (4.1) | Экспе-римент | Пересчет по зависимостям (4.1) | Экспе-римент | Пересчет по зависимостям (4.1) |
| 0,01 | 10 | 0,31 | 9,8 (9,9) | 0,19 | 190/200*** | 0,608 | 19,22/20* |
| 0,02 | 20 | 0,44 | 13,9 (14) | 0,273 | 273 | 0,62 | 19,6 |
| 0,04 | 40 | 0,63 | 19,9 (20) | 0,28 | 280 | 0,45 | 14,2 |
| 0,05 | 50 | 0,7 | 22,13 (22) | 0,36 | 360 | 0,57 | 18,0 |
| 0,1 | 100 | 0,99 | 31,3 (22) | 0,52 | 520 | 0,53 | 16,8 |
| 0,2 | 200 | 1,4 | 44,2 (22) | 0,6 | 600 | 0,433 | 13,7 |
| 0,3 | 300 | 1,7 | 53,8 (22) | 0,44 | 440 | 0,26 | 8,22/(5-8)** |
* - значения, полученные с помощь теоретических зависимостей [124],** - значения, приведенные в работе [30] при h = 0,6 ¸ 1 м,*** - значения, приведенные в работе [47] при h = 0,6 м.
Данные экспериментов после пересчета на натуру с помощью зависимостей (1) сопоставлены с расчетными данными, полученными с помощью зависимостей (4, 5), а также с данными других исследователей (см. табл. 6.1).
На основе полученных таким образом значений параметров ИГВ проводилась оценка несущей способности ледяного покрова путем расчета максимальных изгибных напряжений в сплошном льду. Исходя из теории изгиба жестких пластин [110], напряженное состояние ледяного покрова определяется следующими зависимостями:
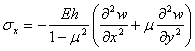 .
.
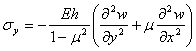 (6.6)
(6.6)
![]() ,
,
где:![]() - модуль Юнга, МПа;
- модуль Юнга, МПа;
![]() - коэффициент Пуассона.
- коэффициент Пуассона.
При этом составляющие ![]() ,
, ![]() ,
, ![]() определяют соответствующую кривизну срединной плоскости пластины. Если принять за
определяют соответствующую кривизну срединной плоскости пластины. Если принять за ![]() ,
,![]() - радиусы кривизны в направлениях осей x и y соответственно, то их выражения будут иметь вид:
- радиусы кривизны в направлениях осей x и y соответственно, то их выражения будут иметь вид:
![]() - кривизна чаши прогиба пластины в направлении оси x;
- кривизна чаши прогиба пластины в направлении оси x;
![]() - кривизна чаши прогиба пластины в направлении оси y.
- кривизна чаши прогиба пластины в направлении оси y.
Однако, полученные экспериментальные данные (см. рис. 6.7) позволяют судить только о кривизне ледяного покрова вблизи траектории движения нагрузки в направлении оси x. Поэтому определение несущей способности ледяного покрова проводилось на основе зависимости для максимальных напряжений в поперечном сечении пластины при цилиндрическом изгибе, что вполне обосновано работами [30, 22, 162]:
![]() (6.7)
(6.7)
где: k - волновое число; A - амплитуда ИГВ; h - толщина ледяного покрова.
Т.о., при использовании выражения (6.7) полагалось, что деформация ледяного покрова в условиях ИГР имеет форму, близкую к цилиндрической. Для обоснования приемлемости такого допущения был проведен анализ, основанный на расчете с использованием зависимостей работы [124]. Расчет показал, что соотношения составляющих деформаций (![]() к
к ![]() ) при
) при ![]() принимают значения
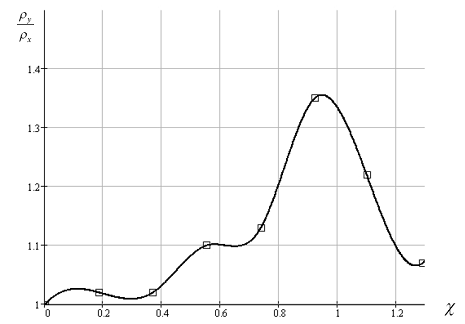
принимают значения ![]() (см. рис. 6.10).
(см. рис. 6.10).
На основании этих данных можно сделать вывод, что при разрушении ледяного покрова в условиях ИГР кривизна профиля ИГВ под нагрузкой в направлении оси y в 1,3 – 1,4 раза меньше кривизны в направлении оси x. Отсюда следует, что в начале трещины возникают при достижении изгибных напряжений ![]() предела прочности льда при изгибе
предела прочности льда при изгибе ![]() .
.
 .
.
Рис. 6.10. Отношения радиусов кривизны от величины .
Это подтверждается характером разрушений, наблюдавшихся в ходе проведения полунатурных и натурных экспериментов с естественным ледяным покровом (см. рис. 6.11, 6.12). На рисунках видно, что сквозные магистральные трещины, образовавшиеся вследствие движения нагрузки с резонансной скоростью, имеют форму близкую к прямолинейной, располагаются приблизительно перпендикулярно к траектории движения вблизи нагрузки и потом закругляются при удалении от нее. Такая ориентация трещин характерна для разрушения ледяного покрова в условиях цилиндрического изгиба либо близкому к нему деформированному состоянию. Таким образом, на основе приведенных теоретических и экспериментальных данных можно сделать заключение о пригодности зависимости (6.7) для определения несущей способности ледяного покрова, находящегося в условиях ИГР.
 .
.
Рис. 6.11. Характер разрушения ледяного покрова в случае резонансного режима движения мотодельтаплана.
 .
.
Рис. 6.12. Характер разрушения сплошного льда СВП «Voyager».
Применяя зависимость (6.7) для исследования несущей способности ледяного покрова в качестве критерия разрушения, можно использовать первую теорию прочности, которая используется при одноосном напряженном состоянии. В соответствии с данной теорией разрушение ледяного покрова происходит в случае, когда действующие напряжения ![]() достигают или превысят предел прочности льда при изгибе
достигают или превысят предел прочности льда при изгибе ![]() :
:
![]() (6.8)
(6.8)
Тогда для сохранения несущей способности ледяного покрова необходимо:
![]() (6.9)
(6.9)
Используя выражения (6.7) и (6.9), получим условие сохранения несущей способности в виде:
![]() (6.10)
(6.10)
Условие (6.10) в графической форме представлено на рис. 6.13, с помощью которого несущую способность ледяного покрова можно оценить следующим образом:
- используя данные модельных экспериментов, представленные в форме, аналогичной рис. 6.7, определяют амплитудуA и длину ![]() ИГВ;
ИГВ;
- с использованием зависимостей (6.1) пересчитывают данные характеристики на натуру и рассчитывают значения n для ![]() , наиболее вероятного для заданных ледовых условий и толщины льда h.
, наиболее вероятного для заданных ледовых условий и толщины льда h.
- в зависимости от найденного значения n на основании рис. 6.13 делают заключение о состоянии несущей способности ледяного покрова.
Приведенная методика может быть использована для оценки несущей способности натурального ледяного покрова на основании данных модельных экспериментов с использованием модели неразрушаемого льда.
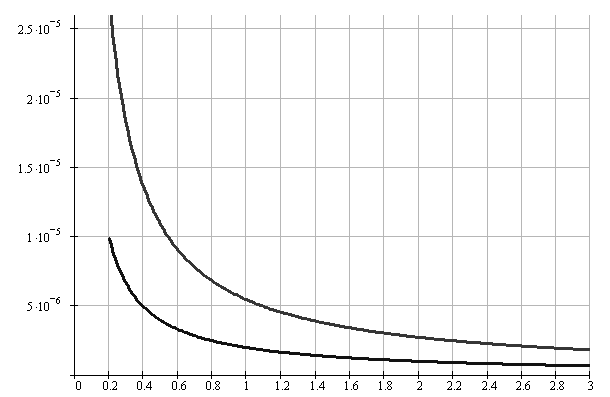
В соответствии с (6.10) на рисунке 6.13 можно выделить 3 зоны характеризующие несущую способность ледяного покрова:
1. Зона сохранения несущей способности - когда действующие напряжения в ледяном покрове ![]() меньше предела прочности при изгибе
меньше предела прочности при изгибе ![]() , или приближаются к нему (кривая I). Вероятность появления трещин при движении нагрузки тем выше, чем ближе значение n к кривой I;
, или приближаются к нему (кривая I). Вероятность появления трещин при движении нагрузки тем выше, чем ближе значение n к кривой I;
2. Область между кривыми I и II - зона, для которой действующие напряжения ![]() близки или равны пределу прочности льда при изгибе
близки или равны пределу прочности льда при изгибе ![]() . При расположении экспериментальных значений n в данной области будет наблюдаться появление сквозных трещин, а при приближении n к кривой II – их раскрытие;
. При расположении экспериментальных значений n в данной области будет наблюдаться появление сквозных трещин, а при приближении n к кривой II – их раскрытие;
 .
.
Рис. 6.13 Зависимость отношения параметра n от толщины ледяного покрова h, для диапазона ![]() [92].
[92].
 .
.
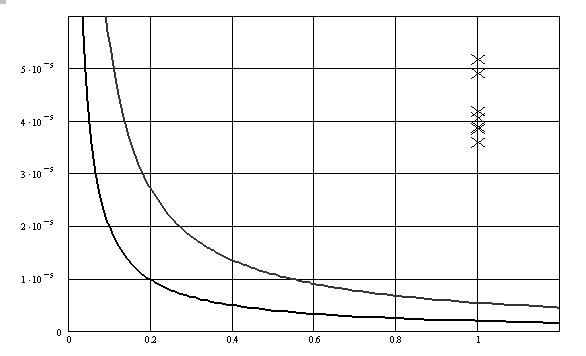
Рис. 6.14. Сравнение теоретических зависимостей и экспериментальных данных в случае влияния ширины акватории. Показаны: 1 – кривые, соответствующие графикам на рис. 6.13; 2 – экспериментальные данные после пересчета на натуру.
3. Зона полного разрушения ледяного покрова – при нахождении значения n в области выше кривой II будет происходить полная потеря несущей способности ледяного покрова вследствие разделения его на обломки (в этом случае несущая способность будет определяться архимедовыми силами).
В частности, можно отметить, что после сравнения экспериментальных данных, полученных в ходе модельных экспериментов с использованием модели неразрушаемого ледяного покрова, с данными графиков на рис. 6.13. можно прийти к выводу, что в ходе экспериментов были смоделированы ИГВ, при которых смоделированный реальный ледяной покров будет разрушаться (см. рис. 6.14), поскольку полученные значения n располагаются в зоне полного разрушения ледяного покрова ![]() см. [58].
см. [58].
Эти экспериментальные данные также были использованы для учета влияния исследуемых ледовых условий на несущую способность ледяных взлетно-посадочных полос.