Научная электронная библиотека

Монографии, изданные в издательстве Российской Академии Естествознания

Прикладные задачи динамики ледяного покрова

Козин В. М., Жесткая В. Д., Погорелова А. В., Чижиумов С. Д., Джабраилов М. Р., Морозов В. С., Кустов А. Н.,

6.3.2. Исследование влияния ширины акватории на параметры ИГВ

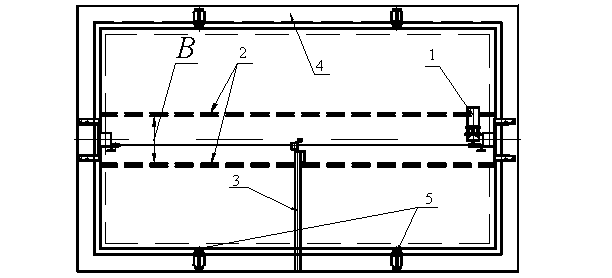
С целью исследования влияния близости берегов замерзших водоемов (узких каналов, рек и заливов) на параметры ИГВ, возникающих в системе лед-вода при воздействии самолета на этапе рулежки, проводилась буксировка ролика весом 0,25 Н по поверхности модельного слоя, расположенного между вертикальными пластинами со скоростью, близкой к резонансной V_р. Траектория движения ролика была симметричной относительно вертикальных пластин. Глубина воды определялась высотой пластин, положением подвесного дна и в опытах составляла м. Резонансная скорость движения груза, соответствующая максимальным амплитудам ИГВ, была определена опытным путем и составляла V_р » 1 м/с. В ходе экспериментов изменялась ширина канала за счет увеличения расстояния между вертикальными пластинами B (рис. 6.16).

.

Рис. 6.16. Схема экспериментальной установки для исследования влияния ширины водоема на параметры ИГВ. 1 – электродвигатель буксировочной системы; 2 – вертикальные пластины; 3 – датчик перемещений; 4 – планширь чаши бассейна; 5 – кронштейны для крепления подвесного дна.

В результате экспериментов были получены профили ИГВ вблизи линии движения нагрузки для различных значений B = 0,2., 0,3., 0,4., 0,5., 0,6., 0,7 м. Кроме экспериментальных исследований, были проведены расчеты с помощью численной модели. Данные расчеты проводились с целью сопоставления теоретических и экспериментальных данных исследований влияния близости берегов на параметры ИГВ.

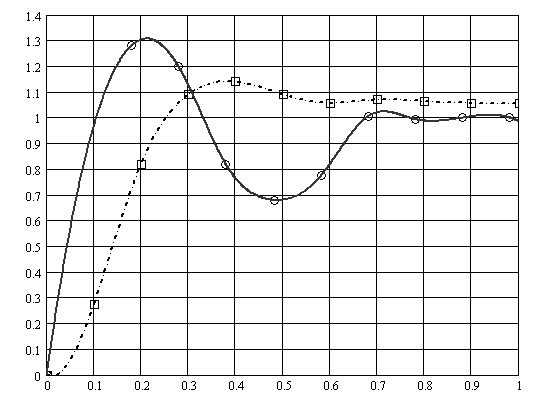
Сравнение теоретических и экспериментальных данных показало качественное (см. рис.6.17), а для длин ИГВ (см. рис.6.18) и количественное соответствие полученных результатов. Для проведения дальнейшего анализа, а также практического использования полученных данных они были приведены к безразмерному виду: , , где , - значения амплитуд и длин ИГВ в случае влияния близости берегов; , - значения амплитуд и длин ИГВ при отсутствии такого влияния. Из полученных зависимостей (рис.6.17,6.18) следует, что близость берегов существенно влияет на параметры возникающих ИГВ. Такое влияние проявлялось в большей степени в диапазоне изменения расстояний м. Начиная с ширины м и более влияние близости берегов не наблюдалось. При этом максимумы амплитуды и длины ИГВ имели место при м. В сравнении со значениями параметров ИГВ при отсутствии влияния берегов амплитуда увеличивалась примерно в 1,3 раза, а длина - в 1,8 раза.

.

Рис.6.17. Зависимость относительной амплитуды ИГВ от ширины водоема B. (1 – теоретическая кривая; 2 – экспериментальная кривая).

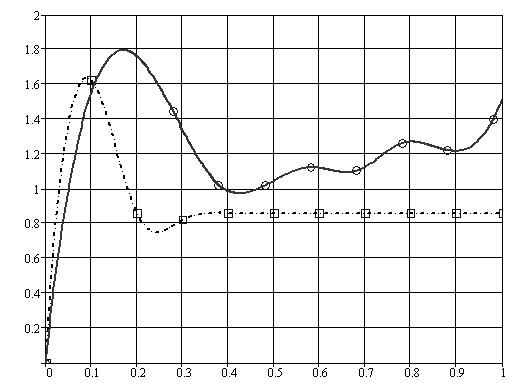
Некоторое несоответствие теории и эксперимента можно объяснить отличиями граничных условий при проведении расчетов и опытов. Так, при выполнении расчетов принималась жесткая заделка кромок ледяной пластины по контуру и полное отсутствие перетекания жидкости на дне по границам расчетной области, т.е. рассматривался ограниченный объем воды.

При проведении экспериментов имевшаяся техническая оснастка не позволила достаточно жестко закрепить модельный слой на вертикальных пластинах, что допускало некоторое смещение его кромок относительно поверхностей мест закрепления. Между вторым дном и ребрами пластин имелся зазор вследствие свободной постановки пластины на дно, что делало его частично проницаемым по бортам, т.е. процесс физического моделирования не в полной мере соответствовал численной модели. По-видимому, это и сказалось на обнаруженном количественном несоответствии при одновременном качественном совпадении.

.

Рис. 6.18. Зависимость относительной длины волны l_r от ширины канала B. (1 – теоретическая кривая, 2 – экспериментальная кривая).

Влияние ограниченности объема воды на параметры ИГВ было обнаружено и для водоема, имеющего размеры близкие к реальным. На рис. 6.19 представлен график зависимости относительной амплитуды ИГВ от ширины канала B, полученный с помощью численного расчета для следующих размеров водоема: ширина канала B = 100…1400 м, глубина акватории H = 10 м, протяженность участка вдоль оси движения 1500 м. Принималась жесткая заделка ледяного покрова по всему периметру берегов. На рисунке видно, что изменение амплитуды имеет такой же характер, как в случае модельного эксперимента с максимумом при м. Следовательно, полученное качественное соответствие теоретических и экспериментальных данных подтверждает работоспособность методики моделирования и достоверность полученных результатов, что дает право на использование установленной закономерности при разработке рекомендаций для пилотов, совершающих посадку (взлет) в условиях водоема с близко расположенными друг относительно друга берегами.

.

Рис. 6.19. Теоретическая зависимость относительной амплитуды натурных ИГВ от ширины водоема B.

На основании зависимостей (6.9, 6.10), и экспериментальных данных, получено условие, позволяющее учесть влияние близости берегов на напряженно-деформированное состояние ледяного покрова, а следовательно, на сохранение его несущей способности:

(6.12)

Зависимость приведена к безразмерному виду и представлена на рис. рис. 6.20, где приведен график зависимости (где - значение выражения (6.12) для случая влияния близости берегов, n - соответствующее значение для случая отсутствия влияния при ) от ширины акватории B.

.

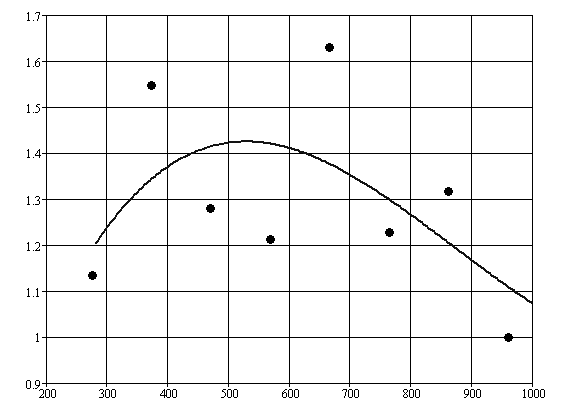
Рис.6.20. Зависимость от ширины акватории B.

Исследованные значения ширины B пересчитаны на натуру с помощью зависимостей (6.1). Полученные результаты показывают, что близость берегов, как и следовало ожидать, оказывает значительное влияние на параметры возникающих ИГВ и при некоторых значениях B приводит к увеличению величины n в 1,4…1,6 раза и соответствующему увеличению напряжений в ледяном покрове. Это влияние носит нелинейный характер, а значения n становятся макимальными в диапазоне м. Т.о., наиболее интенсивное нагружение ледяного покрова реального замерзшего водоема с размерами, соответствующими смоделированным при эксперименте, наиболее вероятно для расстояния между берегами 300 – 700 м, т.е. расстоянию между берегами для реки средних размеров.